ACM-ICPC 2018 南京赛区网络预赛 J题Sum(线性筛素数)

题目链接：https://nanti.jisuanke.com/t/30999

参考自博客：https://kuangbin.github.io/2018/09/01/2018-ACM-ICPC-Nanjing-online-J/

题目中文：

1000毫秒
512000K

无方形整数是一个整数，除了1以外的任何平方数都不可分这个数。例如，6 = 2 *3，6=2*3，6是无方形整数，但12 = 2 ^ 2*3，,因为2 ^ 2是正方形数。有些整数可以分解为两个无方形整数的乘积，可能有多种分解方式。例如，6=1·6=6·1=2·3=3·2，n=a*b和n=b*a被认为是不同的。f （n ）是分解方式的数量n=a*b。问题在于计算

输入

第一行包含一个整数，表示的测试用例的数量。

对于每个测试用例，第一行有一个整数

产量

对于每个测试用例，打印答案

暗示

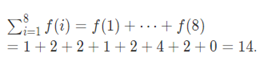
样例输入复制

样例输出复制

解题思路：首先我们对f（n）分析，我们知道对于任意一个数，我们都可以把他拆分成若干素因子乘积的形式如f(n)=p^x+q^y+……r^z，如果f（n）的素因子分解式子中，某个素因子的指数大于二，则f(n)就一定为0；比如f(8)=f(2^3)=0;

如果f(n)非0，则f(n)的素因子的指数只能为1或者2了，如果该素因子的指数为1，则对结果的贡献度为2（即其余素因子分成两部分，可加入任意一边），如果该素因子的指数为1，则对结果的贡献度为1（其余素因子分成两部分，一边一个）；

所有如果单独求一个f(n)的话，只需要对n进行素因素分解。

但是现在需要求1∼2×10^7的f(n), 我们需要进行递推。

假如我们知道n的最小素因子是p的话，而且p的指数是x的话，即n=y*p^x.

那么很显然，如果x == 1, 那么f(n)=2×f(y), 如果x == 2, 那么f(n)=f(y), 如果x > 2, 那么f(n)=0.

然后这里就这要用线性筛素数了，而筛素数的同时记录每个最小的素因子。

附上代码：

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll maxn=2e7;

int prime[maxn+],minprime[maxn+];

ll cnt[maxn+];

//线性筛素数

void getprime()

{

    memset(prime,,sizeof(prime));

    int tot=;

    for(int i=;i<=maxn;i++)

    {

        if(!prime[i])

        {

            prime[tot++]=i;

            minprime[i]=i;

        }

        for(int j=;j<tot&&i*prime[j]<=maxn;j++)

        {

            prime[i*prime[j]]=;

            minprime[i*prime[j]]=prime[j];

            if(i%prime[j]==)

            break;

        }

    }

}

int main()

{

    getprime();

    cnt[]=;

    for(int i=;i<=maxn;i++)

    {

        int x=minprime[i];  //最小素因子

        if(i%(x*x*x)==) cnt[i]=;  //最小素因子指数大于2

        else if(i%(x*x)==) cnt[i]=cnt[i/(x*x)]; //最小素因子指数等于2

        else cnt[i]=*cnt[i/x];  //最小素因子指数为1

    }

    for (int i=;i<=maxn;i++)

        cnt[i]+=cnt[i-];

    int t;

    scanf("%d",&t);

    while(t--)

    {

        int n;

        scanf("%d",&n);

        printf("%lld\n",cnt[n]);

    }

    return ;

}