2019icpc南京网络赛

---

B. super_log（扩展欧拉函数）

题意：求a^a...（b个a）模M的值。

思路：递归用欧拉函数求解，我们知道欧拉降幂公式：

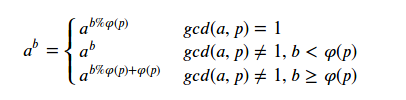
如果讨论b和φ(p)的关系会很麻烦，网上证明了一种精妙的方法，只需重新Mod，就能把a和p当作互素处理，从而统一处理。

要注意的点是：快速幂中取模也要用重写的Mod，最终的答案要%M，递归终点为b=0，如果终点为b=1时，当b=0会WA。

AC代码：

#include<cstdio>
#include<algorithm>
#include<bitset>
using namespace std;

typedef long long LL;
const int maxn=1e6+;
int T;
LL a,b,M,eu[maxn];

void eular(){
    eu[]=;
    for(int i=;i<maxn;++i)
        if(!eu[i])
            for(int j=i;j<maxn;j+=i){
                if(!eu[j]) eu[j]=j;
                eu[j]=eu[j]/i*(i-);
            }
}

LL Mod(LL x,LL M){
    return x<M?x:x%M+M;
}

LL qpow(LL a,LL b,LL M){
    LL ret=;
    while(b){
        if(b&) ret=Mod(ret*a,M);
        a=Mod(a*a,M);
        b>>=;
    }
    return ret;
}

LL dfs(LL b,LL M){
    if(b==) return Mod(,M);
    if(M==) return Mod(a,M);
    return qpow(a,dfs(b-,eu[M]),M);
}

int main(){
    eular();
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld%lld",&a,&b,&M);
        printf("%lld\n",dfs(b,M)%M);
    }
    return ;
}

---

H. Holy Grail（Floyd求最短路）

题意：给定一个图，没有多重边和自回路，有负权边，但没有负权环。n个点，m条有向边，n<=300，m<=500，现加入6条边，使得加入的边权最小，并且不会出现负权环。并且保证一定有解。

思路：

　　因为保证一定有解，如果加入的边为(u,v)，那么原图一定有一条v->u的路径。所以我们用floyd求出各点之前的最短路即可，那么新加的边的最小权值就是v到u的最短路的相反数。新加一条边后重新floyd。

AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;

typedef long long LL;
const int maxn=;
const LL inf=0x3f3f3f3f3f3f3f3f;
int T,n,m;
LL dp[maxn][maxn];

void floyd(){
    for(int k=;k<=n;++k)
        for(int i=;i<=n;++i)
            for(int j=;j<=n;++j)
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;++i)
            for(int j=;j<=n;++j)
                dp[i][j]=inf;
        for(int i=;i<=m;++i){
            int x,y;LL w;
            scanf("%d%d%lld",&x,&y,&w);
            dp[++x][++y]=w;
        }
        for(int i=;i<=;++i){
            floyd();
            int x,y;
            scanf("%d%d",&x,&y);
            ++x,++y;
            printf("%lld\n",-1LL*dp[y][x]);
            dp[x][y]=-1LL*dp[y][x];
        }
    }
    return ;
}

---

F. Greedy Sequence（暴力）

题意：化简之后题意就是对于给定排列，求元素i向左向右扩展k个元素后的第一个比i小的元素。

思路：

　　最开始以为是单调队列扩展，后来发现单调队列没法做。后来让队友试了一发主席树，T了。然后我想用set试一试，用set加入窗口大小为k的所有元素，每次求出第一个比它小的元素，顺序求一次，逆序再求一次。抱着T的心态交了一发，竟然过了QAQ，激动坏了，数据也太水了，暴力都能过。

AC代码：

#include<cstdio>
#include<algorithm>
#include<set>
#include<cctype>
using namespace std;

inline int read()
{
    int x=,f=; char ch=;
    while(!isdigit(ch)) {f|=ch=='-';ch=getchar();}
    while(isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=getchar();
    return f?-x:x;
}

const int maxn=1e5+;
int T,n,k,a[maxn],id[maxn],b[maxn],ans[maxn];
set<int> st;

int main(){
    scanf("%d",&T);
    while(T--){
        st.clear();
        scanf("%d%d",&n,&k);
        for(int i=;i<=n;++i){
            a[i]=read();
            id[a[i]]=i;
            b[i]=;
        }
        st.insert(a[]);
        for(int i=;i<=n;++i){
            st.insert(a[i]);
            if(i-k->) st.erase(a[i-k-]);
            if(*(st.begin())==a[i]) continue;
            set<int>::iterator it=st.find(a[i]);
            --it;
            b[i]=max(b[i],*it);
        }
        st.clear();
        st.insert(a[n]);
        for(int i=n-;i>=;--i){
            st.insert(a[i]);
            if(i+k+<=n) st.erase(a[i+k+]);
            if(*(st.begin())==a[i]) continue;
            set<int>::iterator it=st.find(a[i]);
            --it;
            b[i]=max(b[i],*it);
        }
        for(int i=;i<=n;++i)
            if(b[id[i]]==) ans[i]=;
            else ans[i]=ans[b[id[i]]]+;
        for(int i=;i<=n;++i){
            printf("%d",ans[i]);
            if(i!=n) printf(" ");
        }
        printf("\n");
    }
    return ;
}