bzoj4548: 小奇的糖果 题解

题目链接

题解

不包含所有颜色
就强制不选一个颜色

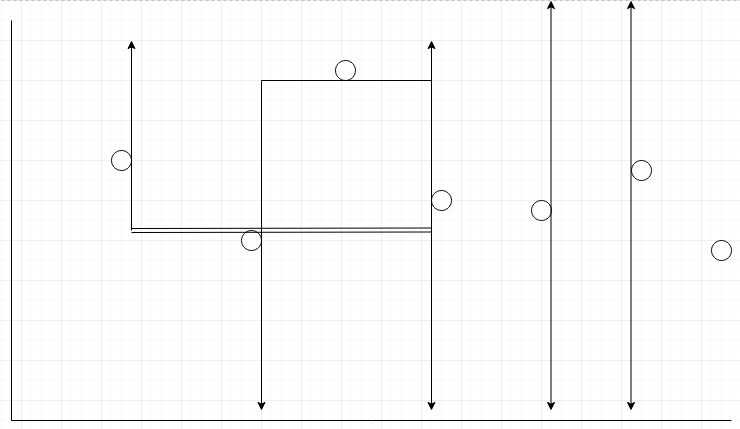
图中圆点颜色相同
矩形越大，包括的点一定不比其一小部分少
如图所示，最大矩形只有3种

离散化\(x\)坐标

然后按\(y\)排序
每次取出颜色的前驱和后继， 算出所围矩形内点的个数，取\(max\)

对于第\(3\)种，扫一遍\(set\)即可

Code

#include<bits/stdc++.h>

#define LL long long
#define RG register

using namespace std;

inline int gi() {
    RG int x = 0; RG char c = getchar(); bool f = 0;
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    if (c == '-') c = getchar(), f = 1;
    while (c >= '0' && c <= '9') x = x*10+c-'0', c = getchar();
    return f ? -x : x;
}
const int N = 100010;
set<int> s[N];
struct node {
    int x, y, z;
    bool operator <(node z) const {
        return y < z.y;
    }
}a[N];
int n, m, b[N], ans;

int t[N];
#define lowbit(x) (x&(-x))
void add(int x, int k) {
    while (x <= n)
        t[x] += k, x += lowbit(x);
    return ;
}
inline int sum(int x) {
    int s = 0;
    while (x > 0) s += t[x], x -= lowbit(x);
    return s;
}

void solve() {
    memset(t, 0, sizeof(t));
    for (int i = 1; i <= m; i++) s[i].clear(), s[i].insert(0), s[i].insert(n+1);
    for (int i = 1,j = 1; i <= n; i = j) {
        while (j <= n && a[i].y == a[j].y) j++;
        for (int k = i; k < j; k++) ans = max(ans, sum(*s[a[k].z].lower_bound(a[k].x)-1)-sum(*--s[a[k].z].upper_bound(a[k].x)));
        for (int k = i; k < j; k++) add(a[k].x, 1), s[a[k].z].insert(a[k].x);
    }
    return ;
}

int main() {
    //freopen(".in", "r", stdin);
    //freopen(".out", "w", stdout);
    int T = gi();
    while (T--) {
        n = gi(), m = gi();
        for (int i = 1; i <= n; i++) a[i].x = gi(), a[i].y = gi(), a[i].z = gi(), b[i] = a[i].x;
        sort(a+1, a+1+n), sort(b+1, b+1+n);
        for (int i = 1; i <= n; i++)
            a[i].x = lower_bound(b+1, b+1+n, a[i].x) - b;
        ans = 0;
        solve();
        for (int i = 1; i <= n>>1; i++) swap(a[i], a[n-i+1]);
        solve();
        for (int i = 1; i <= m; i++)
            for (set<int> :: iterator it = s[i].begin(); it != s[i].end();) {
                int j = *(it++);
                ans = max(ans, sum(*it-1) - sum(j));
                if (j == n+1) break;
            }
        printf("%d\n", ans);
    }
    return 0;
}