Kruskal重构树学习笔记+BZOJ3732 Network

今天学了Kruskal重构树，似乎很有意思的样子~

---

先看题面：

BZOJ

题目大意：$n$ 个点 $m$ 条无向边的图，$k$ 个询问，每次询问从 $u$ 到 $v$ 的所有路径中，最长的边的最小值。

$1\leq n\leq 15000,1\leq m\leq 30000,1\leq k\leq 20000$。

---

我相信你们看见这题的想法和我一样：

货车运输！最小生成树上LCA一下就行了！时间复杂度 $O(m\log m+n\log n+k\log n)$。（这里LCA用倍增。树链剖分复杂度是多一个 $log$ 的）

但是这题有另一种做法：Kruskal重构树。

（这种用到路径最长边值等一般都能用Kruskal重构树）

---

Kruskal重构树是什么？和Kruskal求最小生成树有什么关系？

我们先来看一下Kruskal重构树的一些性质。

Kruskal重构树是由原图的 $n$ 个点，新添加的 $n-1$ 个点和 $2n-2$ 条边构成的树。

（以下讨论的Kruskal重构树都是最小Kruskal重构树，最大Kruskal重构树反之亦然）

下面是一个图和它的Kruskal重构树：（圆点是原图中的点，方点是新加的点）

它的性质有：

1. 一棵二叉树
2. 叶子结点都是原图中的点，没有点权；非叶子结点都是新加的点，有点权
3. 旧点 $u,v$ 两点间（不包括 $u,v$）的所有节点（都是新点）的点权最大值为原图中 $u,v$ 两点间所有路径的最长边的最小值
4. 新点构成一个堆（不一定是二叉堆），在最小Kruskal重构树中是大根堆（最大Kruskal重构树中是小根堆）
5. 结合性质3和4，旧点 $u,v$ 两点的LCA（是新点）权值为原图中 $u,v$ 两点间所有路径的最长边的最小值

比如点 $1,3$ 的LCA权值为 $3$，恰好是原图中 $1,3$ 两点间所有路径的最长边的最小值（边 $(3,5)$）。

---

Kruskal重构树怎么求呢？

1. 找到一条边权最小的，且没有被遍历过的边。
2. 如果这条边连接的两个点目前没有在一个联通块，那么新建一个节点，点权为该边的边权，左右儿子设为这两个点的最远祖先。（通过设置儿子为最远祖先合并联通块且不破坏性质）
3. 重复1,2直到遍历完所有的边。

画个图了解一下，下图中红点是该边连接的两个点，绿点和绿边是添加的点和边：（点我食用这张图会更佳）

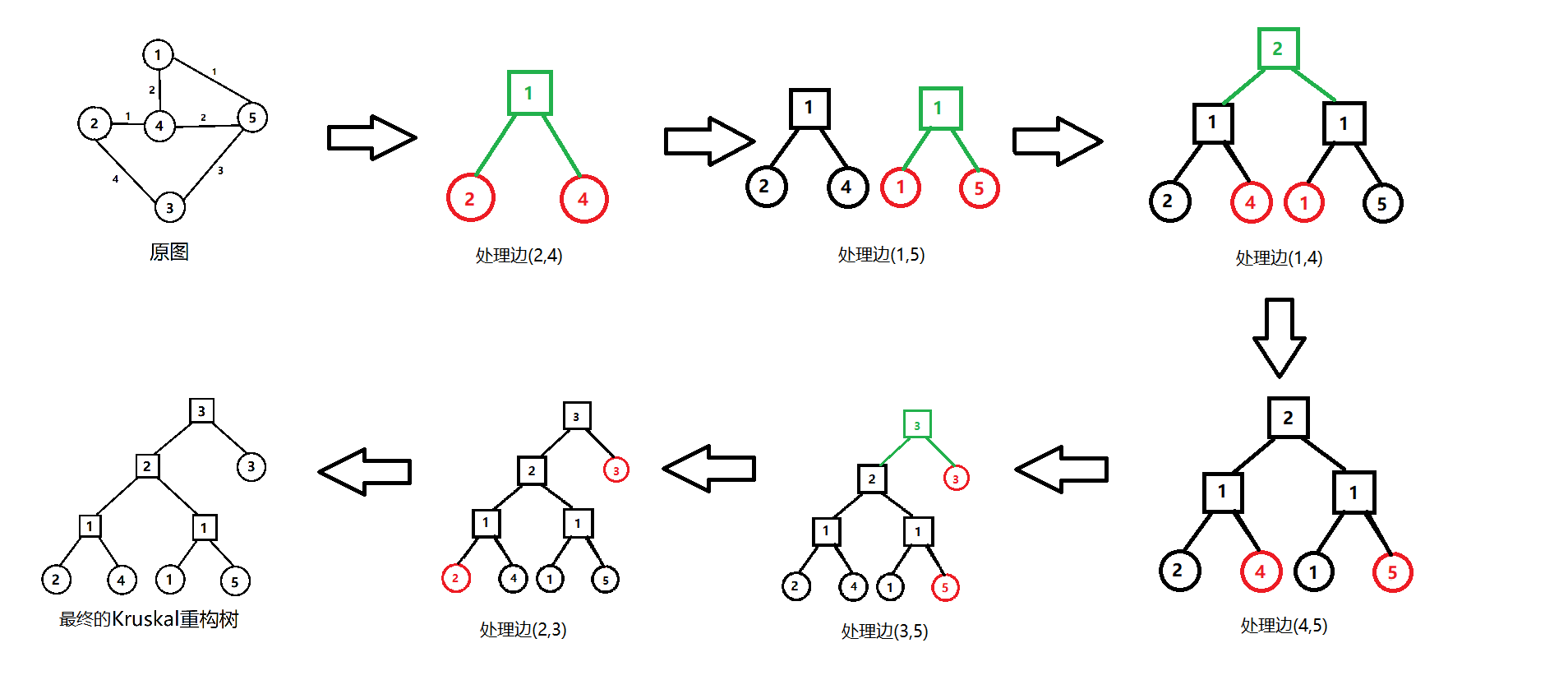
如何用代码实现？像普通的Kruskal一样，维护一个路径压缩并查集，其中 $fa$ 数组不止止是判断在哪个集合，更是标记在重构树上的父亲。这也是为什么要路径压缩而不是按秩合并的原因，因为这样可以更快求得最远祖先。

每处理一条边，先判连通性，如果不连通那么把这两个点的最远祖先的 $fa$ 都设成新加的点，同时连边即可。注意，不能反过来，否则重构树在并查集上的结构会被破坏。

至于旧点之间，怎么连边，连那些边？参见性质2。

（其实就是不用连边，我好啰嗦啊）

---

回到原题：建出最小Kruskal重构树，每次LCA一下即可。

这里顺便说一下，如果原图不保证联通怎么办，如何预处理？（以下的代码中我也判了两点不连通的情况）

两点不连通可以用建Kruskal重构树中的并查集知道。而预处理，每次如果一个点没有dfs到，那么从这个点的最远祖先dfs一遍（也可以用并查集知道）。

为什么要最远祖先呢？因为这样是对的且省时间，均摊 $O(\alpha(n))$。自己感受一下

（洛谷上货车运输那题是有不连通的图的测试点，我写重构树时第一次没有从最远祖先开始dfs，感受一下：）

时间复杂度：若用树链剖分求LCA是 $O(m\log m+n\log n+k\log n)$，复杂度更优。虽然常数大一点，但是学了一个新算法不是很好吗？

（读者：浪费时间，散了散了）

---

代码：（附带判断不连通）

#include<bits/stdc++.h>
using namespace std;
struct edge1{    //一开始的边，方便排序
    int u,v,w;
    bool operator<(const edge1 e)const{
        return w<e.w;
    }
}e1[];
struct edge2{    //重构树上的边（虽然只有两个儿子但这样写舒服）
    int to,nxt;
}e2[];    //重构树的点数是原图的约2倍，但是没有双向边
int n,m,q,el1,el2,cnt,root;
int u_fa[],w[],head[];    //u_fa是并查集的fa，w是新节点的权值
int dep[],fa[],son[],size[],top[];
inline void add1(int u,int v,int w){    //原图加边
    e1[++el1]=(edge1){u,v,w};
}
inline void add2(int u,int v){    //重构树加边
    e2[++el2]=(edge2){v,head[u]};
    head[u]=el2;
}
int getfa(int x){    //路径压缩
    return x==u_fa[x]?x:u_fa[x]=getfa(u_fa[x]);
}
void dfs1(int u,int f){
    fa[u]=f;
    dep[u]=dep[f]+;
    size[u]=;
    int maxson=-;
    for(int i=head[u];i;i=e2[i].nxt){
        int v=e2[i].to;
        if(v==fa[u]) continue;
        dfs1(v,u);
        size[u]+=size[v];
        if(size[v]>maxson) maxson=size[v],son[u]=v;
    }
}
void dfs2(int u,int topf){
    top[u]=topf;
    if(!son[u]) return;
    dfs2(son[u],topf);
    for(int i=head[u];i;i=e2[i].nxt){
        int v=e2[i].to;
        if(v==fa[u] || v==son[u]) continue;
        dfs2(v,v);
    }
}
int calc(int u,int v){
    if(getfa(u)!=getfa(v)) return -;    //如果不连通
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        u=fa[top[u]];
    }
    return dep[u]<dep[v]?w[u]:w[v];    //LCA的权值
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add1(u,v,w);
    }
    sort(e1+,e1+m+);    //从小到大排序
    for(int i=;i<=*n-;i++) u_fa[i]=i;
    cnt=n;
    for(int i=;i<=m;i++){
        int u=e1[i].u,v=e1[i].v;    //操作的两个点
        u=getfa(u);v=getfa(v);
        if(u==v) continue;    //已经联通，跳过
        w[++cnt]=e1[i].w;    //新建一个点
        u_fa[u]=u_fa[v]=cnt;    //设置父亲！
        add2(cnt,u);add2(cnt,v);    //加边（不需要双向边）
    }
    for(int i=;i<=cnt;i++) //只需要遍历存在的点（图不连通的话点数可能没到2n-1）
        if(!dep[i])    //如果这个点没有被搜过
            dfs1(getfa(i),),dfs2(getfa(i),getfa(i));    //那就从最远祖先开始搜
    scanf("%d",&q);
    for(int i=;i<=q;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        printf("%d\n",calc(u,v));
    }
}

另外今年的NOI2018D1T1正解也是Kruskal重构树，以后再慢慢杠吧，留个坑等着补题解。