洛谷—— P2047 社交网络

P2047 社交网络

题目描述

在社交网络（social network）的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有n个人，人与人之间有不同程度的关系。我 们将这个关系网络对应到一个n个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值c，c越小，表示两 个人之间的关系越密切。

我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度，注意到最短路径上的其他结点为s和t的联系提供了某种便利， 即这些结点对于s 和t之间的联系有一定的重要程度。我们可以通过统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。

考虑到两个结点A和B之间可能会有多条最短路径。我们修改重要程度的定义如下：

令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s到t的最短路的数目；则定义

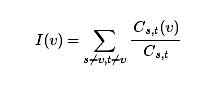
为结点v在社交网络中的重要程度。

为了使I(v)和Cs,t(v)有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。

现在给出这样一幅描述社交网络s的加权无向图，请你求出每一个结点的重要程度。

输入输出格式

输入格式：

输入第一行有两个整数，n和m，表示社交网络中结点和无向边的数目。在无向图中，我们将所有结点从1到n进行编号。

接下来m行，每行用三个整数a, b, c描述一条连接结点a和b，权值为c的无向边。注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

输出格式：

输出包括n行，每行一个实数，精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。

输入输出样例

输入样例#1：

4 4
1 2 1
2 3 1
3 4 1
4 1 1

输出样例#1：

1.000
1.000
1.000
1.000

说明

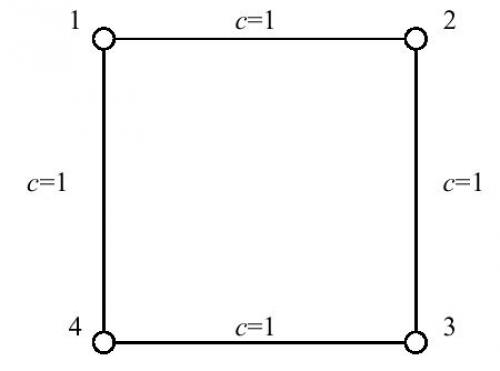
对于1号结点而言，只有2号到4号结点和4号到2号结点的最短路经过1号结点，而2号结点和4号结点之间的最短路又有2条。因而根据定义，1号结点的重要程度计算为1/2+1/2=1。由于图的对称性，其他三个结点的重要程度也都是1。

50%的数据中：n ≤10，m ≤45

100%的数据中：n ≤100，m ≤4 500，任意一条边的权值c是正整数，满足：1 ≤c ≤1 000。

所有数据中保证给出的无向图连通，且任意两个结点之间的最短路径数目不超过10^10。

思路：

其实，这道题还是挺水的、、、

差不多为Floyd+组合数学、、

我们先用Floyd处理出从一个节点到另一个节点的最短路，在处理最短路的时候顺便把从一个节点到另一个节点最短路的条数处理出来。

像这样、、

for(int k=1;k<=n;k++)
     for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
       {
            if(dis[i][j]>dis[i][k]+dis[k][j])
         {
            dis[i][j]=dis[i][k]+dis[k][j];//更改最短路
            f[i][j]=f[i][k]*f[k][j];//这个地方与下面都是跟组合数学相关，自己领会一下吧。。。
         }
            else if(dis[i][j]==dis[i][k]+dis[k][j]) f[i][j]+=f[i][k]*f[k][j];//忘了写else一直不过样例，后来才知道原来写不写else是不一样的，因为我们在执行完第一步后，就满足了这个条件，就会执行这一步
       }//如果这两条路的长度相同的话则均为最短路，那么就要加上之前的了、、、

在最后处理答案的时候

  if(i!=k&&j!=k&&dis[i][j]==dis[i][k]+dis[k][j]&&f[i][j]) //这个地方的dis[i][j]==dis[i][k]+dis[k][j]可以说明这一条路一定经过k这个节点，为什么？！因为你在更新最短路的时候用它更新的啊！所以最短路一定经过他啊！            ans=ans+(double)f[i][k]*f[k][j]/f[i][j];//题目给出的定义

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 210
#define maxn 99999999
using namespace std;
long long f[N][N];
int n,m,x,y,z,dis[N][N];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int begin()
{
    ;i<=n;i++)
     ;j<=n;j++)
      dis[i][j]=(i!=j)*maxn;
}
int main()
{
    n=read(),m=read();
    begin(); double ans;
    ;i<=m;i++)
    {
        x=read(),y=read(),z=read();
        f[x][y]=f[y][x]=;
        dis[x][y]=dis[y][x]=z;
    }
    ;k<=n;k++)
     ;i<=n;i++)
      ;j<=n;j++)
       {
            if(dis[i][j]>dis[i][k]+dis[k][j])
         {
            dis[i][j]=dis[i][k]+dis[k][j];
            f[i][j]=f[i][k]*f[k][j];
         }
            else if(dis[i][j]==dis[i][k]+dis[k][j]) f[i][j]+=f[i][k]*f[k][j];
       }
    ;k<=n;k++)
    {
       ans=;
       ;i<=n;i++)
         ;j<=n;j++)
          if(i!=k&&j!=k&&dis[i][j]==dis[i][k]+dis[k][j]&&f[i][j])
           ans=ans+(double)f[i][k]*f[k][j]/f[i][j];
       printf("%.3lf\n",ans);
    }
    ;
}