JavaScript中常见数据结构
数据结构
- 栈:一种遵从先进后出 (LIFO) 原则的有序集合;新添加的或待删除的元素都保存在栈的末尾,称作栈顶,另一端为栈底。在栈里,新元素都靠近栈顶,旧元素都接近栈底。
- 队列:与上相反,一种遵循先进先出 (FIFO / First In First Out) 原则的一组有序的项;队列在尾部添加新元素,并从头部移除元素。最新添加的元素必须排在队列的末尾。
- 链表:存储有序的元素集合,但不同于数组,链表中的元素在内存中并不是连续放置的;每个元素由一个存储元素本身的节点和一个指向下一个元素的引用(指针/链接)组成。
- 集合:由一组无序且唯一(即不能重复)的项组成;这个数据结构使用了与有限集合相同的数学概念,但应用在计算机科学的数据结构中。
- 字典:以 [键,值] 对为数据形态的数据结构,其中键名用来查询特定元素,类似于 Javascript 中的
Object。 - 散列:根据关键码值(Key value)直接进行访问的数据结构;它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度;这个映射函数叫做散列函数,存放记录的数组叫做散列表。
- 树:由 n(n>=1)个有限节点组成一个具有层次关系的集合;把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的,基本呈一对多关系,树也可以看做是图的特殊形式。
- 图:图是网络结构的抽象模型;图是一组由边连接的节点(顶点);任何二元关系都可以用图来表示,常见的比如:道路图、关系图,呈多对多关系。
栈

生活中常见的Stack的例子比如一摞书,你最后放上去的那本你之后会最先拿走;又比如浏览器的访问历史,当点击返回按钮,最后访问的网站最先从历史记录中弹出。
Stack一般具备以下方法:
- push:将一个元素推入栈顶
- pop:移除栈顶元素,并返回被移除的元素
- peek:返回栈顶元素
- isEmpty(): 栈中是否有元素
- clear(): 移除栈中所有元素
- size:返回栈中元素的个数
以对象形式实现栈
<script type="text/javascript">
function Stack() {
this.count = 0;
this.storage = {};
//将一个元素推入栈顶
this.push = function (value) {
this.storage[this.count] = value;
this.count++;
}
//移除栈顶元素,并返回被移除的元素
this.pop = function () {
if (this.count === 0) {
return undefined;
}
this.count--;
var result = this.storage[this.count];
delete this.storage[this.count];
return result;
}
//返回栈顶元素
this.peek = function () {
return this.storage[this.count - 1];
}
//栈中是否有元素
this.isEmpty = function () {
//使用es6语法判断对象中属性长度
//return Object.keys(this.storage).length==0;
return this.count==0;
}
//移除栈中所有元素
this.clear = function () {
this.count = 0
//return this.storage={};
}
//返回栈中元素的个数
this.size = function () {
return this.count;
}
} var newStack = new Stack();
newStack.push("第一个元素");
newStack.push("第二个元素");
newStack.push("第三个元素");
console.log("打印栈中元素个数:" + newStack.size());
console.log("打印栈中栈顶元素:" + newStack.peek());
console.log("打印栈中移除元素:" + newStack.pop());
console.log("移除栈顶元素后再次打印栈中栈顶元素:" + newStack.peek());
console.log("判断栈中是否有元素:" + newStack.isEmpty());
console.log("移除栈中所有元素:" + newStack.clear());
console.log("移除后判断栈中是否有元素:" + newStack.isEmpty());
console.log("打印栈中移除元素:" + newStack.pop());
</script>
以数组形式实现栈
<script type="text/javascript">
function Stack() {
//保存栈内元素的数组
this.dataStore = [];
//top用来记录栈顶位置,初始化为0
this.top = 0; this.push = function (element) {
this.dataStore[this.top++] = element; // 先在top位置加入元素,之后top加1
}
this.pop = function () {
// top先减1,然后返回top位置的元素
return this.dataStore[--this.top];
}
this.peek = function peek() {
return this.dataStore[this.top - 1];
} this.isEmpty = function clear() {
return this.top ==0;
} this.clear = function clear() {
this.top = 0;
} this.length = function length() {
return this.top;
}
}
var newStack = new Stack();
newStack.push("第一个元素");
newStack.push("第二个元素");
newStack.push("第三个元素");
console.log("打印栈中元素个数:" + newStack.length());
console.log("打印栈中栈顶元素:" + newStack.peek());
console.log("打印栈中移除元素:" + newStack.pop());
console.log("移除栈顶元素后再次打印栈中栈顶元素:" + newStack.peek());
console.log("判断栈中是否有元素:" + newStack.isEmpty());
console.log("移除栈中所有元素:" + newStack.clear());
console.log("移除后判断栈中是否有元素:" + newStack.isEmpty());
</script>
Queue(队列)

Queue和Stack有一些类似,不同的是Stack是先进后出,而Queue是先进先出。Queue在生活中的例子比如排队上公交,排在第一个的总是最先上车;又比如打印机的打印队列,排在前面的最先打印。
Queue一般具有以下常见方法:
- enqueue:入列,向队列尾部增加一个元素
- dequeue:出列,移除队列头部的一个元素并返回被移除的元素
- front:获取队列的第一个元素
- isEmpty:判断队列是否为空
- size:获取队列中元素的个数
Javascript中的Array已经具备了Queue的一些特性,所以我们可以借助Array实现一个Queue类型:
<script type="text/javascript">
function Queue() {
var collection = [];
//返回队列所有元素
this.print = function () {
return collection;
}
//入列,向队列尾部增加一个元素
this.enqueue = function (element) {
collection.push(element);
}
//出列,移除队列头部的一个元素并返回被移除的元素
this.dequeue = function () {
return collection.shift();
}
//获取队列的第一个元素
this.front = function () {
return collection[0];
}
//判断队列是否为空
this.isEmpty = function () {
return collection.length === 0;
}
//清除队列
this.clear = function () {
items = [];
};
//获取队列中元素的个数
this.size = function () {
return collection.length;
}
}
var newQueue= new Queue();
newQueue.enqueue("第一个元素");
newQueue.enqueue("第二个元素");
newQueue.enqueue("第三个元素");
console.log("打印队列中元素个数:" + newQueue.size());
console.log("打印队列中第一个元素:" + newQueue.front());
console.log("打印队列中所有元素:" + newQueue.print());
console.log("打印队列中移除元素:" + newQueue.dequeue());
console.log("移除队列元素后再次打印队列中所有元素:" + newQueue.print());
console.log("判断队列中是否有元素:" + newQueue.isEmpty());
console.log("移除队列中所有元素:" + newQueue.clear());
console.log("移除后判断队列中是否有元素:" + newQueue.isEmpty());
</script>
Priority Queue(优先队列)
Queue还有个升级版本,给每个元素赋予优先级,优先级高的元素入列时将排到低优先级元素之前。区别主要是enqueue方法的实现:
<script type="text/javascript">
function PriorityQueue() {
var collection = [];
//返回队列所有元素
this.print = function () {
return collection;
}
//入列,向队列尾部增加一个元素
this.enqueue = function (element) {
collection.push(element);
}
//出列,移除队列头部的一个元素并返回被移除的元素
this.dequeue = function () {
return collection.shift();
}
//获取队列的第一个元素
this.front = function () {
return collection[0];
}
//判断队列是否为空
this.isEmpty = function () {
return collection.length === 0;
}
//清除队列
this.clear = function () {
items = [];
};
//获取队列中元素的个数
this.size = function () {
return collection.length;
}
//优先队列
this.priorityEnqueue = function (element) {
if (this.isEmpty()) {
collection.push(element);
} else {
var added = false;
for (var i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element);
added = true;
break;
}
}
if (!added) {
collection.push(element);
}
}
}
}
var newQueue = new PriorityQueue();
newQueue.enqueue("第一个元素");
newQueue.enqueue("第二个元素");
newQueue.enqueue("第三个元素");
console.log("打印队列中元素个数:" + newQueue.size());
console.log("打印队列中第一个元素:" + newQueue.front());
console.log("打印队列中所有元素:" + newQueue.print());
console.log("打印队列中移除元素:" + newQueue.dequeue());
console.log("移除队列元素后再次打印队列中所有元素:" + newQueue.print());
console.log("判断队列中是否有元素:" + newQueue.isEmpty());
console.log("移除队列中所有元素:" + newQueue.clear());
console.log("移除后判断队列中是否有元素:" + newQueue.isEmpty()); newQueue.priorityEnqueue(['gannicus', 3]);
newQueue.priorityEnqueue(['spartacus', 1]);
newQueue.priorityEnqueue(['crixus', 2]);
newQueue.priorityEnqueue(['oenomaus', 4]); console.log("优先队列中所有元素:" + newQueue.print()); </script>
Linked List(链表)
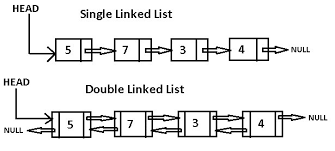
链表是一种链式数据结构,链上的每个节点包含两种信息:节点本身的数据和指向下一个节点的指针。链表和传统的数组都是线性的数据结构,存储的都是一个序列的数据,但也有很多区别,如下表:
| 比较维度 | 数组 | 链表 |
|---|---|---|
| 内存分配 | 静态内存分配,编译时分配且连续 | 动态内存分配,运行时分配且不连续 |
| 元素获取 | 通过Index获取,速度较快 | 通过遍历顺序访问,速度较慢 |
| 添加删除元素 | 因为内存位置连续且固定,速度较慢 | 因为内存分配灵活,只有一个开销步骤,速度更快 |
| 空间结构 | 可以是一维或者多维数组 | 可以是单向、双向或者循环链表 |
一个单向链表通常具有以下方法:
- size:返回链表中节点的个数
- head:返回链表中的头部元素
- add:向链表尾部增加一个节点
- remove:删除某个节点
- indexOf:返回某个节点的index
- elementAt:返回某个index处的节点
- addAt:在某个index处插入一个节点
- removeAt:删除某个index处的节点
单向链表的Javascript实现:
<script type="text/javascript">
/**
* 链表中的节点
*/
function Node(element) {
// 节点中的数据
this.element = element;
// 指向下一个节点的指针
this.next = null;
} function LinkedList() {
var length = ;
var head = null;
//返回链表中节点的个数
this.size = function () {
return length;
}
//返回链表中的头部元素
this.head = function () {
return head;
}
//向链表尾部增加一个节点
this.add = function (element) {
var node = new Node(element);
if (head == null) {
head = node;
} else {
var currentNode = head; while (currentNode.next) {
currentNode = currentNode.next;
} currentNode.next = node;
}
length++;
}
//删除某个节点
this.remove = function (element) {
var currentNode = head;
var previousNode;
if (currentNode.element === element) {
head = currentNode.next;
} else {
while (currentNode.element !== element) {
previousNode = currentNode;
currentNode = currentNode.next;
}
previousNode.next = currentNode.next;
}
length--;
} this.isEmpty = function () {
return length === ;
} //返回链表所有节点
this.value = function () {
var currentNode = head;
var nodeList = [];
if (currentNode==null) {
return undefined
} else {
while (currentNode.next) {
nodeList.push(currentNode.element);
currentNode = currentNode.next;
}
nodeList.push(currentNode.element);
}
return nodeList;
} //返回某个节点的index
this.indexOf = function (element) {
var currentNode = head;
var index = -;
while (currentNode) {
index++;
if (currentNode.element === element) {
return index;
}
currentNode = currentNode.next;
} return -;
}
//返回某个index处的节点
this.elementAt = function (index) {
var currentNode = head;
var count = ;
while (count < index) {
count++;
currentNode = currentNode.next;
}
return currentNode.element;
}
//在某个index处插入一个节点
this.addAt = function (index, element) {
var node = new Node(element);
var currentNode = head;
var previousNode;
var currentIndex = ; if (index > length) {
return false;
} if (index === ) {
node.next = currentNode;
head = node;
} else {
while (currentIndex < index) {
currentIndex++;
previousNode = currentNode;
currentNode = currentNode.next;
}
node.next = currentNode;
previousNode.next = node;
}
length++;
}
//删除某个index处的节点
this.removeAt = function (index) {
var currentNode = head;
var previousNode;
var currentIndex = ;
if (index < || index >= length) {
return null;
}
if (index === ) {
head = currentIndex.next;
} else {
while (currentIndex < index) {
currentIndex++;
previousNode = currentNode;
currentNode = currentNode.next;
}
previousNode.next = currentNode.next;
}
length--;
return currentNode.element;
}
} var newLinkedList = new LinkedList();
newLinkedList.indexOf("第一个节点");
newLinkedList.add("第一个节点");
newLinkedList.add("第二个节点");
newLinkedList.add("第三个节点");
newLinkedList.add("第四个节点");
newLinkedList.add("第五个节点");
newLinkedList.add("第六个节点");
newLinkedList.add("第七个节点");
newLinkedList.add("第八个节点");
console.log("打印链表中所有元素:" + newLinkedList.value());
newLinkedList.remove("第一个节点");
newLinkedList.remove("第三个节点");
console.log("打印删除后链表中所有元素:" + newLinkedList.value());
</script>
单链表
talk is easy, show the code, 下面用 JavaScript 实现一个相对完整的单链表,并提供以下方法供调用:
- push(element) // 链表尾部插入节点
- pop() // 链表尾部删除节点
- shift() // 删除头部节点、
- unshift(element) // 插入头部节点
- find(index) // 查找指定位置节点
- insert(element, index) // 指定位置插入节点
- edit(element, index) // 修改指定位置节点
- delete(index) // 链表删除指定位置节点
- cycle() // 使链表首尾成环
function initList() {
class Node {
constructor(item) {
this.element = item
}
}
class List {
constructor() {
this.head = null
this.size =
this.last = null
}
/**
* 链表查找元素
* @param index 查找的位置
*/
find(index) {
let current = this.head
for (let i = ; i < index; i++) {
current = current.next
}
return current
}
/**
* 链表尾部插入元素
* @param element 插入的元素
*/
push(element) {
let newNode = new Node(element)
if (this.size === ) {
this.head = newNode
this.head.next = null
this.last = this.head
} else {
this.last.next = newNode
this.last = newNode
newNode.next = null
}
this.size +=
}
/**
* 链表尾部删除元素
* @param element 删除的位置
*/
pop(element) {
this.last.next = null
}
/**
* 链表头部删除元素
*/
shift() {
if (this.size === )
return
this.head = this.head.next
if (this.size === )
this.last = null
this.size -=
}
/**
* 链表头部插入元素
* @param element 插入的元素
*/
unshift(element) {
let newNode = new Node(element)
newNode.next = this.head
this.head = newNode
if (this.size === )
this.last = this.head
this.size +=
}
/**
* 链表插入元素
* @param element 插入的位置, index 插入的位置
*/
insert(element, index) {
if (index < || index > this.size) {
console.error('超出链表节点范围')
return
}
let newNode = new Node(element)
if (this.size === ) {
// 空链表
newNode.next = null
this.head = newNode
this.last = newNode
} else if (index === ) {
// 插入头部
newNode.next = this.head
this.head = newNode
} else if (index == this.size) {
//插入尾部
newNode.next = null
this.last.next = newNode
this.last = newNode
} else {
// 中间插入
let preNode = this.find(index - )
newNode.next = preNode.next
preNode.next = newNode
}
this.size +=
}
/*
*链表编辑元素
* @param element 编辑的元素,index 元素位置
*/
edit(element, index) {
let current = this.find(index)
current.element = element
}
/*
*链表删除元素
* @param index 删除元素位置
*/
delete(index) {
let current = this.find(index)
if (index === ) {
// 删除头节点
this.head = this.head.next
} else if (index === ((this.size) - )) {
// 删除尾节点
let preNode = this.find(index - )
preNode.next = null
} else {
// 删除中间节点
let preNode = this.find(index - )
let nextNode = preNode.next.next
let removeNode = preNode.next
preNode.next = nextNode
}
this.size -=
}
/*
*链表使首尾成环
*/
cycle() {
this.last.next = this.head
}
}
return new List()
}
let list = initList()
双向链表
双向链表的特点就是添加了指向上一个节点的指针(prev),比较单链表来说,稍微复杂一些,也更强大,这里把上面的单链表修改一下。
function initList() {
class Node {
constructor(item) {
this.element = item
this.next = null
this.prev = null
}
}
class List {
constructor() {
this.head = null
this.size =
this.last = null
}
/**
* 链表查找元素
* @param index 查找的位置
*/
find(index) {
let current = this.head
for (let i = ; i < index; i++) {
current = current.next
}
return current
}
/**
* 链表尾部插入元素
* @param element 插入的元素
*/
push(element) {
let newNode = new Node(element)
if (this.size === ) {
this.head = newNode
this.head.next = null
this.last = this.head
} else {
this.last.next = newNode
newNode.next = null
newNode.prev = this.last
this.last = newNode
}
this.size +=
}
/**
* 链表尾部删除元素
* @param element 删除的位置
*/
pop() {
if (this.size === )
return
if (this.size === ) {
this.head = null
this.last = null
} else {
this.last.prev.next = null
this.last = this.last.prev
}
this.size -=
}
/**
* 链表头部删除元素
*/
shift() {
if (this.size === )
return
if (this.size === ) {
this.head = null
this.last = null
} else {
this.head = this.head.next
this.head.prev = null
}
this.size -=
}
/**
* 链表头部插入元素
* @param element 插入的元素
*/
unshift(element) {
let newNode = new Node(element)
if (this.size === ) {
this.head = newNode
this.head.next = null
this.last = this.head
} else {
this.head.prev = newNode
newNode.next = this.head
this.head = newNode
}
this.size +=
}
/**
* 链表插入元素
* @param element 插入的位置, index 插入的位置
*/
insert(element, index) {
if (index < || index > this.size) {
console.error('超出链表节点范围')
return
}
let newNode = new Node(element)
if (this.size === ) {
// 空链表
this.head = newNode
this.head.next = null
this.last = this.head
} else if (index === ) {
// 插入头部
this.head.pre = newNode
newNode.next = this.head
this.head = newNode
} else if (index == this.size - ) {
//插入尾部
newNode.next = null
newNode.prev = this.last
this.last.next = newNode
this.last = newNode
} else {
// 中间插入
let prevNode = this.find(index - )
newNode.next = prevNode.next
prevNode.next = newNode
newNode.prev = prevNode
newNode.next.prev = newNode
}
this.size +=
}
/*
*链表编辑元素
* @param element 编辑的元素,index 元素位置
*/
edit(element, index) {
let current = this.find(index)
current.element = element
}
/*
*链表删除元素
* @param index 删除元素位置
*/
delete(index) {
let current = this.find(index)
if (index === ) {
// 删除头节点
this.head = this.head.next
this.prev = null
} else if (index === ((this.size) - )) {
// 删除尾节点
let preNode = this.find(index - )
preNode.next = null
} else {
// 删除中间节点
let preNode = this.find(index - )
let nextNode = preNode.next.next
let removeNode = preNode.next
preNode.next = nextNode
nextNode.prev = preNode
}
this.size -=
}
/*
*链表使首尾成环
*/
cycle() {
this.last.next = this.head
this.head.prev = this.last
}
}
return new List()
}
let list = new initList()
循环链表
循环链表可以是单链表也可以是双向链表,它的特点是最后一个节点的 next 指针指向的是 head 节点
而不是 null,上面代码已经提供了 cycle 方法来实现。
判断链表有环
主要有这些方法:
遍历链表,使每一个节点与之前节点比较,若有重复则为有环链表
定义一个 Map 对象,遍历链表到每一个节点,若 Map 中没有次节点 ID,则将节点 ID 为 key, 存入 Map ,每个节点判断一次,如果某个节点的 ID存在,证明链表成环
双指针法,举个例子来说,两个人在操场跑步,速度不同时,总会在某些时刻相遇,就是因为跑到是圆的(环),利用这个原理,定义一个循环和两个指向头节点的指针,一个每次移动一个节点,一个移动两个节点,如果是成环的链表,某个时刻必然会遇到同一个节点。
链表在前端开发中的应用
链表的特性表明其擅长修改,不擅查找,所以对于需要大量修改的操作,可以考虑用链表实现,但是前端往往处理的数据量不会大,所以这种场景的实际意义不是很大,个人感觉在框架的底层优化上,使用较多,业务开发中,数组够用。
链表因为是随机存储的,所以比较省内存,但是对动态语言 JavaScript 解释器来说,有自动的垃圾回收机制来管理内存,所以链表的这个优势就不明显了。
链表特殊的结构,感觉适合做轮播图(双向循环链表)、双向导航列表等
Set(集合)
集合是数学中的一个基本概念,表示具有某种特性的对象汇总成的集体。在ES6中也引入了集合类型Set,Set和Array有一定程度的相似,不同的是Set中不允许出现重复的元素而且是无序的。
一个典型的Set应该具有以下方法:
- values:返回集合中的所有元素
- size:返回集合中元素的个数
- has:判断集合中是否存在某个元素
- add:向集合中添加元素
- remove:从集合中移除某个元素
- union:返回两个集合的并集
- intersection:返回两个集合的交集
- difference:返回两个集合的差集
- subset:判断一个集合是否为另一个集合的子集
使用Javascript可以将Set进行如下实现,为了区别于ES6中的Set命名为MySet:
function MySet() {
var collection = [];
this.has = function (element) {
return (collection.indexOf(element) !== -1);
}
this.values = function () {
return collection;
}
this.size = function () {
return collection.length;
}
this.add = function (element) {
if (!this.has(element)) {
collection.push(element);
return true;
}
return false;
}
this.remove = function (element) {
if (this.has(element)) {
index = collection.indexOf(element);
collection.splice(index, 1);
return true;
}
return false;
}
this.union = function (otherSet) {
var unionSet = new MySet();
var firstSet = this.values();
var secondSet = otherSet.values();
firstSet.forEach(function (e) {
unionSet.add(e);
});
secondSet.forEach(function (e) {
unionSet.add(e);
});
return unionSet;
}
this.intersection = function (otherSet) {
var intersectionSet = new MySet();
var firstSet = this.values();
firstSet.forEach(function (e) {
if (otherSet.has(e)) {
intersectionSet.add(e);
}
});
return intersectionSet;
}
this.difference = function (otherSet) {
var differenceSet = new MySet();
var firstSet = this.values();
firstSet.forEach(function (e) {
if (!otherSet.has(e)) {
differenceSet.add(e);
}
});
return differenceSet;
}
this.subset = function (otherSet) {
var firstSet = this.values();
return firstSet.every(function (value) {
return otherSet.has(value);
});
}
}
最后,推荐大家使用Fundebug,一款很好用的BUG监控工具~
Hash Table(哈希表/散列表)
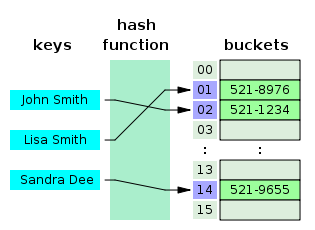
Hash Table是一种用于存储键值对(key value pair)的数据结构,因为Hash Table根据key查询value的速度很快,所以它常用于实现Map、Dictinary、Object等数据结构。如上图所示,Hash Table内部使用一个hash函数将传入的键转换成一串数字,而这串数字将作为键值对实际的key,通过这个key查询对应的value非常快,时间复杂度将达到O(1)。Hash函数要求相同输入对应的输出必须相等,而不同输入对应的输出必须不等,相当于对每对数据打上唯一的指纹。
一个Hash Table通常具有下列方法:
- put()增加元素
- remove()移除元素
- get()获取元素
简易版本的Hash Table的Javascript实现
class HashTable{
constructor(){
this.table = [] // 散列表
}
/* 散列函数1:冲突相对比较 */
loseloseHashCode(key){ // 通过ASCII码转换生成key
let hash =
for (let i = ; i< key.length; i++) {
hash += key[i].charCodeAt() // 计算key的ASCII码,当使用2个不同的键值,通过散列函数生成一致的散列键值,这样会发生哈希碰撞,导致数据覆盖
}
return hash% // loseloseHashCode方法计算关键码的公式,即 ASCII码取余37
}
/* 新增元素 */
put(key,value){
const position = this.loseloseHashCode(key) // 元素在散列表里的地址
this.table[position] = value
}
/* 移除元素 */
remove(key){
this.table[this.loseloseHashCode(key)] = undefined
}
/* 获取元素 */
get(key){
return this.table[this.loseloseHashCode(key)]
}
}
function betterHash (str, arr) {
var H = ;
var total = ;
for (var i = ; i < str.length; i++) {
total += H * total + str.chatCodeAt(i);
}
total = total % arr.length;
return parseInt(total);
}
function get (key) {
return this.table[this.betterHash(key, this.table)];
}
质数37是一个比较好的数字适合我们的哈希算法来参与哈希键值运算,并且使生成的键值在哈希表中均匀分布。
以对象实现哈希表
// 创建构造函数HashTable
function HashTable() {
// 初始化哈希表的记录条数size
var size = ; // 创建对象用于接受键值对
var res = {}; // 添加关键字,无返回值
this.add = function (key, value) { //判断哈希表中是否存在key,若不存在,则size加1,且赋值
if (!this.containKey(key)) {
size++;
} // 如果之前不存在,赋值; 如果之前存在,覆盖。
res[key] = value;
}; // 删除关键字, 如果哈希表中包含key,并且delete返回true则删除,并使得size减1
this.remove = function (key) {
if (this.containKey(key) && (delete res[key])) {
size--;
}
}; // 哈希表中是否包含key,返回一个布尔值
this.containKey = function (key) {
return (key in res);
}; // 哈希表中是否包含value,返回一个布尔值
this.containValue = function (value) { // 遍历对象中的属性值,判断是否和给定value相等
for (var prop in res) {
if (res[prop] === value) {
return true;
}
}
return false;
}; // 根据键获取value,如果不存在就返回null
this.getValue = function (key) {
return this.containKey(key) ? res[key] : null;
}; // 获取哈希表中的所有value, 返回一个数组
this.getAllValues = function () {
var values = [];
for (var prop in res) {
values.push(res[prop]);
}
return values;
}; // 根据值获取哈希表中的key,如果不存在就返回null
this.getKey = function (value) {
for (var prop in res) {
if (res[prop] === value) {
return prop;
}
} // 遍历结束没有return,就返回null
return null;
}; // 获取哈希表中所有的key,返回一个数组
this.getAllKeys = function () {
var keys = [];
for (var prop in res) {
keys.push(prop);
}
return keys;
}; // 获取哈希表中记录的条数,返回一个数值
this.getSize = function () {
return size;
}; // 清空哈希表,无返回值
this.clear = function () {
size = ;
res = {};
};
}
Tree(树)
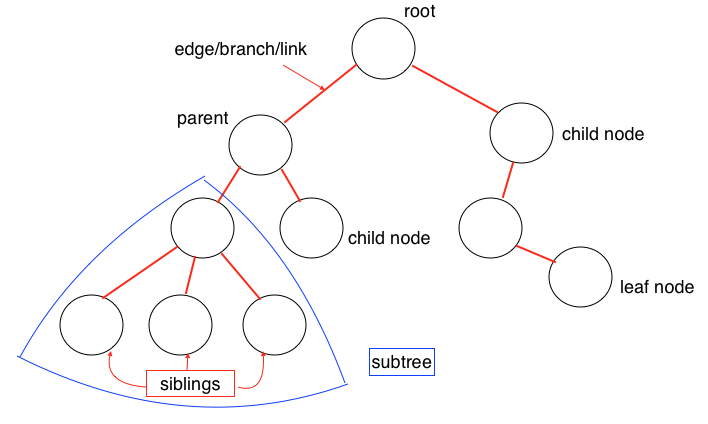
Tree的数据结构和自然界中的树极其相似,有根、树枝、叶子,如上图所示。Tree是一种多层数据结构,与Array、Stack、Queue相比是一种非线性的数据结构,在进行插入和搜索操作时很高效。在描述一个Tree时经常会用到下列概念:
Root(根):代表树的根节点,根节点没有父节点
Parent Node(父节点):一个节点的直接上级节点,只有一个
Child Node(子节点):一个节点的直接下级节点,可能有多个
Siblings(兄弟节点):具有相同父节点的节点
Leaf(叶节点):没有子节点的节点
Edge(边):两个节点之间的连接线
Path(路径):从源节点到目标节点的连续边
Height of Node(节点的高度):表示节点与叶节点之间的最长路径上边的个数
Height of Tree(树的高度):即根节点的高度
Depth of Node(节点的深度):表示从根节点到该节点的边的个数
Degree of Node(节点的度):表示子节点的个数
以二叉查找树为例,展示树在Javascript中的实现。在二叉查找树中,即每个节点最多只有两个子节点,而左侧子节点小于当前节点,而右侧子节点大于当前节点,如图所示:
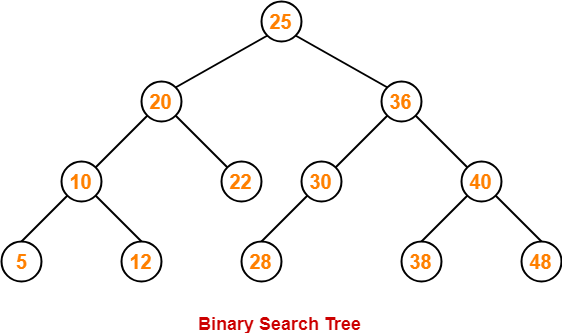
二叉查找树应该具有以下常用方法:
- add:向树中插入一个节点
- findMin:查找树中最小的节点
- findMax:查找树中最大的节点
- find:查找树中的某个节点
- isPresent:判断某个节点在树中是否存在
- remove:移除树中的某个节点
以下是二叉查找树的Javascript实现:
class Node {
constructor(data, left = null, right = null) {
this.data = data;
this.left = left;
this.right = right;
}
}
class BST {
constructor() {
this.root = null;
}
add(data) {
const node = this.root;
if (node === null) {
this.root = new Node(data);
return;
} else {
const searchTree = function (node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data);
return;
} else if (node.left !== null) {
return searchTree(node.left);
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data);
return;
} else if (node.right !== null) {
return searchTree(node.right);
}
} else {
return null;
}
};
return searchTree(node);
}
}
findMin() {
let current = this.root;
while (current.left !== null) {
current = current.left;
}
return current.data;
}
findMax() {
let current = this.root;
while (current.right !== null) {
current = current.right;
}
return current.data;
}
find(data) {
let current = this.root;
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right;
}
if (current === null) {
return null;
}
}
return current;
}
isPresent(data) {
let current = this.root;
while (current) {
if (data === current.data) {
return true;
}
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return false;
}
remove(data) {
const removeNode = function (node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// node没有子节点
if (node.left == null && node.right == null) {
return null;
}
// node没有左侧子节点
if (node.left == null) {
return node.right;
}
// node没有右侧子节点
if (node.right == null) {
return node.left;
}
// node有两个子节点
var tempNode = node.right;
while (tempNode.left !== null) {
tempNode = tempNode.left;
}
node.data = tempNode.data;
node.right = removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) {
node.left = removeNode(node.left, data);
return node;
} else {
node.right = removeNode(node.right, data);
return node;
}
}
this.root = removeNode(this.root, data);
}
}
测试一下:
const bst = new BST(); bst.add(4); |
打印结果:
1 |
二叉树的遍历,遍历方式:
前序遍历:先遍历根结点,然后左子树,再右子树
中序遍历:先遍历左子树,然后根结点,再右子树
后续遍历:先遍历左子树,然后右子树,再根结点
//前序遍历
function ProOrderTraverse(biTree) {
if (biTree == null) return;
console.log(biTree.data);
ProOrderTraverse(biTree.lChild);
ProOrderTraverse(biTree.rChild);
} //中序遍历
function InOrderTraverse(biTree) {
if (biTree == null) return;
InOrderTraverse(biTree.lChild);
console.log(biTree.data);
InOrderTraverse(biTree.rChild);
} //后续遍历
function PostOrderTraverse(biTree) {
if (biTree == null) return;
PostOrderTraverse(biTree.lChild);
PostOrderTraverse(biTree.rChild);
console.log(biTree.data);
}
二叉树的非递归遍历
深度优先遍历(主要利用栈的先进后出)
广度优先遍历(主要利用队列的先进先出)
//深度优先非递归
function DepthFirstSearch(biTree) {
let stack = [];
stack.push(biTree); while (stack.length != ) {
let node = stack.pop();
console.log(node.data);
if (node.rChild) {
stack.push(node.rChild);
}
if (node.lChild) {
stack.push(node.lChild);
} } } //广度优先非递归
function BreadthFirstSearch(biTree) {
let queue = [];
queue.push(biTree);
while (queue.length != ) {
let node = queue.shift();
console.log(node.data);
if (node.lChild) {
queue.push(node.lChild);
}
if (node.rChild) {
queue.push(node.rChild);
}
} }
Trie(字典树,读音同try)
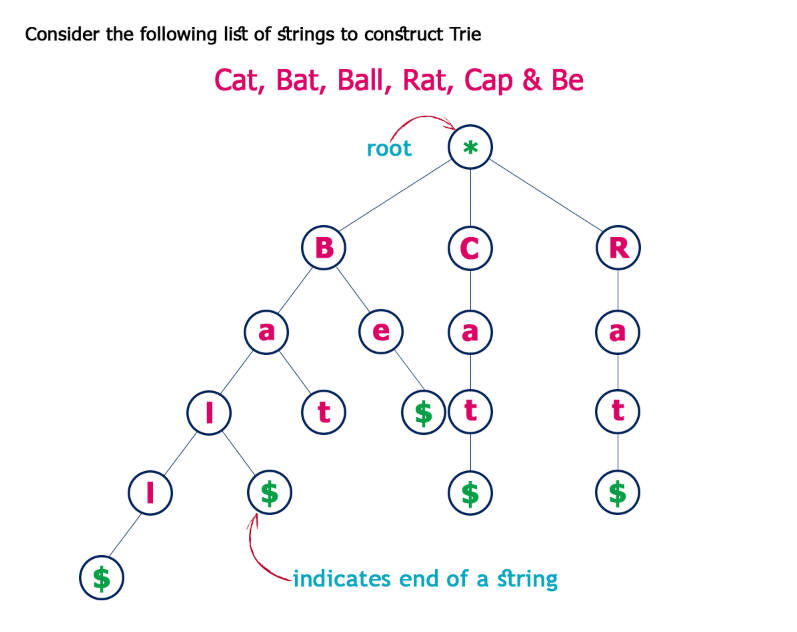
Trie也可以叫做Prefix Tree(前缀树),也是一种搜索树。Trie分步骤存储数据,树中的每个节点代表一个步骤,trie常用于存储单词以便快速查找,比如实现单词的自动完成功能。 Trie中的每个节点都包含一个单词的字母,跟着树的分支可以可以拼写出一个完整的单词,每个节点还包含一个布尔值表示该节点是否是单词的最后一个字母。
Trie一般有以下方法:
- add:向字典树中增加一个单词
- isWord:判断字典树中是否包含某个单词
- print:返回字典树中的所有单词
/**
* Trie的节点
*/
function Node() {
this.keys = new Map();
this.end = false;
this.setEnd = function () {
this.end = true;
};
this.isEnd = function () {
return this.end;
}
} function Trie() {
this.root = new Node(); this.add = function (input, node = this.root) {
if (input.length === 0) {
node.setEnd();
return;
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node());
return this.add(input.substr(1), node.keys.get(input[0]));
} else {
return this.add(input.substr(1), node.keys.get(input[0]));
}
} this.isWord = function (word) {
let node = this.root;
while (word.length > 1) {
if (!node.keys.has(word[0])) {
return false;
} else {
node = node.keys.get(word[0]);
word = word.substr(1);
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false;
} this.print = function () {
let words = new Array();
let search = function (node = this.root, string) {
if (node.keys.size != 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter));
}
if (node.isEnd()) {
words.push(string);
}
} else {
string.length > 0 ? words.push(string) : undefined;
return;
}
};
search(this.root, new String());
return words.length > 0 ? words : null;
}
}
Graph(图)
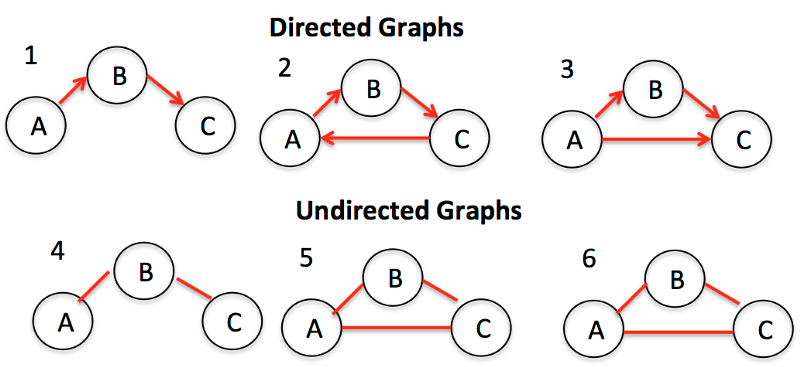
Graph是节点(或顶点)以及它们之间的连接(或边)的集合。Graph也可以称为Network(网络)。根据节点之间的连接是否有方向又可以分为Directed Graph(有向图)和Undrected Graph(无向图)。Graph在实际生活中有很多用途,比如:导航软件计算最佳路径,社交软件进行好友推荐等等。
Graph通常有两种表达方式:
Adjaceny List(邻接列表):
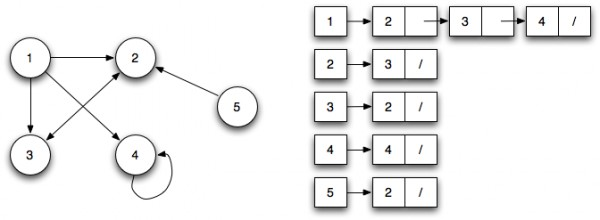
邻接列表可以表示为左侧是节点的列表,右侧列出它所连接的所有其他节点。
和 Adjacency Matrix(邻接矩阵):
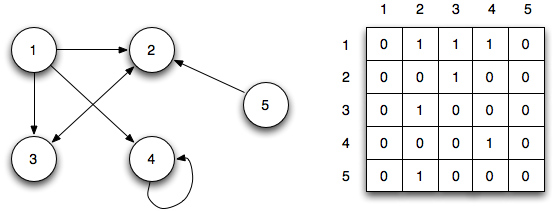
邻接矩阵用矩阵来表示节点之间的连接关系,每行或者每列表示一个节点,行和列的交叉处的数字表示节点之间的关系:0表示没用连接,1表示有连接,大于1表示不同的权重。
访问Graph中的节点需要使用遍历算法,遍历算法又分为广度优先和深度优先,主要用于确定目标节点和根节点之间的距离,
图的相关术语
1.有一条边相连的顶点叫相邻顶点;
2.一个顶点的度就是该顶点的相邻顶点数;
3.路径指顶点组成的连续序列;
4.简单路径没有重复顶点;
5.有向图和无向图
图的表示
邻接矩阵
array[i][j] ===1代表i节点和j节点相邻,否则不相邻
邻接表
相当于把每个节点的相邻节点一一列举出来。
关联矩阵
形式和邻接矩阵一样,只是把邻接矩阵的直接维度换成对应的边,适用于边比顶点多的情况。
创建图类
接下来就采用邻接表的方式创建上面的图并且采用字典来表示:
创建字典类
function Dictionary() {
var items = {};
//set(key,value)向字典里添加新元素,这里主要用来添加边
this.set = function (key, value) {
items[key] = value;
}
//has(key)如果存在就返回true,否则false
this.has = function (key) {
return key in items;
}
//get(key)通过key查找特定的数值并返回,这里主要用来查找顶点对应的边数组
this.get = function (key) {
return this.has(key) ? items[key] : undefined;
}
}
创建图类
function Graph() {
var vertices = []; //用来储存顶点
var adjList = new Dictionary(); //用来储存边
//创建initializeColor用来初始化各个顶点的颜色,为遍历过程中的标记做准备
var initializeColor = function () {
var color = [];
for (var i = ; i < vertices.length; i++) {
color[vertices[i]] = 'white';
}
return color;
}
//addVertex(key)用来添加顶点
this.addVertex = function (v) {
vertices.push(v);
adjList.set(v, []);
}
//addEdge(key,value)用来添加边v-w
this.addEdge = function (v, w) {
adjList.get(v).push(w);
adjList.get(w).push(v);
}
//toString()把邻接表转化成字符串的形式,便于输出显示
this.toString = function () {
var s = '';
for (var i = ; i < vertices.length; i++) {
s += vertices[i] + '->';
var neighbors = adjList.get(vertices[i]);
for (var j = ; j < neighbors.length; j++) {
s += neighbors[j] + ' ';
}
s += '\n';
}
return s;
}
}
创建实例
var graph = new Graph();
var myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
//添加顶点
for (var i = ; i < myVertices.length; i++) {
graph.addVertex(myVertices[i]);
} //逐一加入边
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'G');
graph.addEdge('C', 'D');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
console.log(graph.toString());
输出的结果为:
A->B C D
B->A E F
C->A G D
D->A C G H
E->B I
F->B
G->C D
H->D
I->E
图的遍历
广度优先遍历
采用队列的方式,先添加节点的先被探索;
采用三种颜色来反应节点的状态:
白色:还没被访问;
灰色:被访问但未被探索;
黑色:被访问且探索过;
思路:
首先搜索节点A,探索A节点的相邻节点B,C,D,把其加入队列中,再逐一出队列进行探索,从而实现广度遍历。
添加bfs方法
//广度优先遍历,在Graph()类中添加以下方法
this.bfs = function (v, callback) {
var color = initializeColor(); //初始化节点,都标记为白色
var queue = []; //创建队列用来顶点的入队;
queue.push(v); //访问的节点入队列
while (!queue.length == ) { //如果队列非空就执行以下
var u = queue.shift(); //节点出队列
var neighbors = adjList.get(u); //探索节点对应的边
color[u] = 'grey'; //把搜索过的节点变成灰色
for (var i = ; i < neighbors.length; i++) {
var w = neighbors[i];
if (color[w] === 'white') { //如果探索到的子节点是白色就逐一变灰并入队列
color[w] = 'grey';
queue.push(w);
}
}
color[u] = 'black'; //节点完成搜索和探索的过程,直接变黑
if (callback) {
callback(u); //回调函数,可以用来输出
}
}
}
创建bfs实例
//bfs实例
function printNode(value) {
console.log('Visited vertex:' + value);
}
graph.bfs(myVertices[], printNode);
bfs输出结果
Visited vertex:A
Visited vertex:B
Visited vertex:C
Visited vertex:D
Visited vertex:E
Visited vertex:F
Visited vertex:G
Visited vertex:H
Visited vertex:I
使用BFS寻找最短路径
this.BFS = function (v) {
var color = initializeColor(),
queue = [],
d = [], //用来储存从v到u的距离
pred = []; //用来储存节点的前溯点
queue.push(v);
for (var i = ; i < vertices.length; i++) {
d[vertices[i]] = ; //初始化
pred[vertices[i]] = null;
}
while (!queue.length == ) {
var u = queue.shift();
var neighbors = adjList.get(u);
color[u] = 'grey';
for (i = ; i < neighbors.length; i++) {
var w = neighbors[i];
if (color[w] === 'white') {
color[w] = 'grey';
d[w] = d[u] + ; //从头节点到w的距离
pred[w] = u;
queue.push(w);
}
}
color[u] = 'black';
}
return {
distance: d,
predecessers: pred
}
}
创建BFS实例
//BFS实例
var shortestPathA = graph.BFS(myVertices[]);//需要输入头节点myVertices[0]
//console.log(shortestPathA); //搜索路径BFS
var fromVertex = myVertices[];
for (var i = ; i < myVertices.length; i++) {
var toVertex = myVertices[i];
var path = []; //path用来储存路径
for (var v = toVertex; v !== fromVertex; v = shortestPathA.predecessers[v]) {
path.push(v);
}
path.push(fromVertex);
var s = path.pop();
while (!path.length == ) {
s += '-' + path.pop();
}
console.log(s)
}
BFS输出结果
A-B
A-C
A-D
A-B-E
A-B-F
A-C-G
A-D-H
A-B-E-I
深度优先遍历
采用栈的方式,先添加节点的先被探索;
由递归实现。
思路:
从节点A开始,探索到A的相邻节点B,C,D压入栈中(这里的代码采用for循环,所以没有实质上的栈,但是用栈更容易理解),接着搜索B,探索到B的相邻节点E,F压入栈中,以此递归。
添加dfs方法
this.dfs = function (callback) {
var color = initializeColor();
for (var i = ; i < vertices.length; i++) {
if (color[vertices[i]] === 'white') {
dfsVisit(vertices[i], color, callback)//调用递归函数
}
}
}
var dfsVisit = function (u, color, callback) {
color[u] = 'grey';
if (callback) {
callback(u);
}
var neighbors = adjList.get(u);
for (var i = ; i < neighbors.length; i++) {
var w = neighbors[i];
if (color[w] === 'white') {
dfsVisit(w, color, callback);
}
}
color[u] = 'black';
}
创建dfs实例
graph.dfs(printNode);
dfs输出结果
Visited vertex:A
Visited vertex:B
Visited vertex:E
Visited vertex:I
Visited vertex:F
Visited vertex:C
Visited vertex:G
Visited vertex:D
Visited vertex:H
JavaScript中常见数据结构的更多相关文章
- JavaScript 中常见设计模式整理
开发中,我们或多或少地接触了设计模式,但是很多时候不知道自己使用了哪种设计模式或者说该使用何种设计模式.本文意在梳理常见设计模式的特点,从而对它们有比较清晰的认知. JavaScript 中常见设计模 ...
- JavaScript中常见的数组操作函数及用法
JavaScript中常见的数组操作函数及用法 昨天写了个帖子,汇总了下常见的JavaScript中的字符串操作函数及用法.今天正好有时间,也去把JavaScript中常见的数组操作函数及用法总结一下 ...
- JavaScript中常见的字符串操作函数及用法
JavaScript中常见的字符串操作函数及用法 最近几次参加前端实习生招聘的笔试,发现很多笔试题都会考到字符串的处理,比方说去哪儿网笔试题.淘宝的笔试题等.如果你经常参加笔试或者也是一个过来人,相信 ...
- JavaScript:JavaScript中常见获取对象元素的方法
介绍: javascript中常见的3种获取元素的方法,分别是通过元素ID.通过标签名字和通过类名字来获取 操作如下: 1.getElementById DOM提供了一个名为getElementByI ...
- JavaScript中的数据结构及实战系列
本系列主要是讲解JavaScript中的数据结构及在实际项目中遇到的地方 JavaScript中的数据结构及实战系列(1):队列 JavaScript中的数据结构及实战系列(2):栈
- JavaScript 中常见的内存泄露陷阱(摘)
内存泄露是每个开发者最终都不得不面对的问题.即便使用自动内存管理的语言,你还是会碰到一些内存泄漏的情况.内存泄露会导致一系列问题,比如:运行缓慢,崩溃,高延迟,甚至一些与其他应用相关的问题. 什么是内 ...
- JavaScript中常见的十五种设计模式
在程序设计中有很多实用的设计模式,而其中大部分语言的实现都是基于“类”. 在JavaScript中并没有类这种概念,JS中的函数属于一等对象,在JS中定义一个对象非常简单(var obj = {}), ...
- javascript中的数据结构
Javascript中的关键字 abstract continue finally instanceof private this boolean ...
- javascript中常见的几种循环遍历
项目开发中,不管是建立在哪个框架基础上,对数据的处理都是必须的,而处理数据离不开各种遍历循环.javascript中循环遍历有很多种方式,记录下几种常见的js循环遍历. 一.for循环 for循环应该 ...
随机推荐
- 体验三大JavaScript文件上传库(Uppy.js/Filepond/Dropzone)
最近发现了一个高颜值的前端上传组件Uppy.js,立即上手体验了一波,感觉还不错.然后又看到同类型的Filepond以及Dropzone.js,对比体验了一下,感觉都很优秀,但是在体验过程中,都遇到了 ...
- 图像识别领域的一些code
图像识别领域的一些code 转自:http://blog.163.com/pz124578@126/blog/static/23522694201343110495537/ ps:里面的一些方法都是目 ...
- mysql8中查询语句表别名不能使用 “of”
今天在迁移一个项目的时候,发现有一个sql报错,但是语句跟迁移之前完全一样,所以想来应该是 mysql 版本差异导致的. 迁移之前版本:5.6.28(腾讯云) 迁移之后版本:8.0.16(阿里云) 新 ...
- Go 缓冲信道
缓冲信道 语法结构:cap为容量 ch := make(chan type, cap) 缓冲信道支持len()和cap(). 只能向缓冲信道发送容量以内的数据. 只能接收缓冲信道长度以内的数据. 缓冲 ...
- BP神经网络—java实现
神经网络的结构 神经网络的网络结构由输入层,隐含层,输出层组成.隐含层的个数+输出层的个数=神经网络的层数,也就是说神经网络的层数不包括输入层.下面是一个三层的神经网络,包含了两层隐含层,一个输出层. ...
- vue v-cloak 指令 处理页面显示源码
有时候页面会先出现源码,再显示解析的内容.可以通过v-cloak解决 v-cloak 这个指令会作为元素的一个属性一直保持到vue实例编译结束,即解析后移除此指令. /* 含有v-cloak的html ...
- 【leetcode】610. Triangle Judgement
原题 A pupil Tim gets homework to identify whether three line segments could possibly form a triangle. ...
- sklearn特征工程
目录 一. 特征工程是什么? 2 ①特征使用方案 3 ②特征获取方案 4 ③特征处理 4 1. 特征清洗 4 2. 数据预处理 4 3. 特 ...
- SRX550路由器缓存满了无法在web页面操作解决方法
SRX550路由器缓存满了无法在web页面操作解决方法 首页出现下图为满的标志,我这个文档就是解决这中情况,让web页面可以操作的 1. 打开命令行,输入用户密码,进入路由器 注意:这里使用te ...
- 09_Azkaban案例实践2_Command多job工作流flow
1.Command类型多job工作流flow 1.创建有依赖关系的多个job描述:第一个job:foo.job # foo.job type=command command=echo foo 2.第二 ...