Codeforces Round #653 (Div. 3) A. Required Remainder (数学)

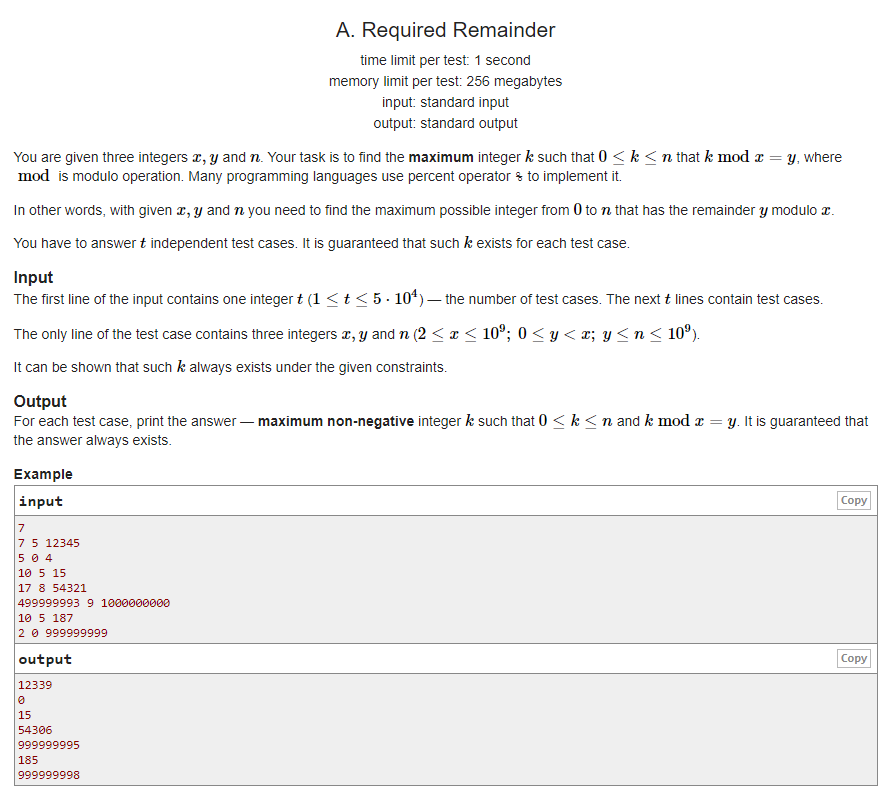
• 题意:有三个正整数\(x,y,n\),再\(1\)~\(n\)中找一个最大的数\(k\),使得\(k\ mod\ x=y\).

• 题解:先记\(tmp=n/x\),再判断\(tmp*x+y\)的值是否大于\(n\),如果是,直接输出\((tmp-1)*x+y\),否则输出\(tmp*x+y\).

  ps:这题好像可以直接二分搞

• 代码:

  int t;
  int x,y,n;
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
      cin>>t;
       while(t--){
          cin>>x>>y>>n;
          int tmp=n/x;
          if(tmp*x+y<=n)
          cout<<tmp*x+y<<endl;
          else{
              cout<<((tmp-1)*x+y)<<endl;
          }
       }
  
      return 0;
  }