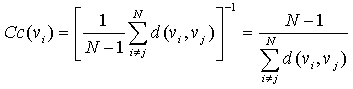社交网络图中结点的“重要性”计算 (30 分) C++解法
社交网络图中结点的“重要性”计算 (30 分)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi 的“紧密度中心性”Cc(vi )数学上定义为vi 到其余所有结点vj (j≠i) 的最短距离d(vi ,vj )的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104 )是图中结点个数,顺便假设结点从1到N编号;M(≤105 )是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
代码:
#include <iostream>
#include <queue>
#include <climits>
#include <map>
using namespace std;
class Graph {
public:
Graph(int v, int e) : Vertex(v), Edge(e) {
G = new int *[v];
for (int i = 0; i < v; i++) {
G[i] = new int[v];
for (int j = 0; j < v; j++) {
G[i][j] = 0;
}
}
}
~Graph(){
for (int i = 0; i < Vertex; i++) {
delete[] G[i];
}
delete[] G;
}
void Insert(int v1, int v2) {
G[v1][v2] = 1;
G[v2][v1] = 1;
}
double Importance(int v) {
int distance[Vertex];
for (int i = 0; i < Vertex; i++) {
distance[i] = INT_MAX;
}
distance[v] = 0;
int Visited[Vertex][Vertex];
for (int i = 0; i < Vertex; i++) {
for (int j = 0; j < Vertex; j++) {
Visited[i][j] = 0;
}
}
map<int,int> visitedNode;
queue<int> q;
q.push(v);
while (!q.empty()) {
int temp = q.front();
q.pop();
for (int i = 0; i < Vertex; i++) {
if (G[temp][i] == 1 && Visited[temp][i] == 0 && visitedNode[i]==0) {
if (distance[i] > distance[temp] + 1)
distance[i] = distance[temp] + 1;
visitedNode[i]=1;
q.push(i);
Visited[temp][i] = 1;
Visited[i][temp] = 1;
}
}
}
double sum = 0;
for (int i = 0; i < Vertex; i++) {
sum += distance[i];
}
return (Vertex - 1.0) / sum;
}
private:
int Vertex;
int Edge;
int **G;
};
int main() {
int vertex, edge;
scanf("%d %d", &vertex, &edge);
Graph graph(vertex, edge);
int temp1, temp2;
for (int i = 0; i < edge; i++) {
scanf("%d %d", &temp1, &temp2);
graph.Insert(temp1 - 1, temp2 - 1);
}
int num;
scanf("%d", &num);
int n;
for (int i = 0; i < num; i++) {
scanf("%d", &n);
printf("Cc(%d)=%.2f\n", n, graph.Importance(n - 1));
}
}
社交网络图中结点的“重要性”计算 (30 分) C++解法的更多相关文章
- PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分)
PTA数据结构与算法题目集(中文) 7-36 社交网络图中结点的“重要性”计算 (30 分) 7-36 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某 ...
- PTA 社交网络图中结点的“重要性”计算(30 分)
7-12 社交网络图中结点的“重要性”计算(30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互 ...
- 7-10 社交网络图中结点的“重要性”计算(30 point(s)) 【并查集+BFS】
7-10 社交网络图中结点的"重要性"计算(30 point(s)) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络 ...
- PTA 7-12(图) 社交网络图中结点的“重要性”计算 最短路
7-12(图) 社交网络图中结点的“重要性”计算 (30 分) 在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来.他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的 ...
- 7-11 社交网络图中结点的“重要性”计算 (30 分)(Dijkstra算法)
题意: 思路:对每个输入的点跑一遍dijkstra算法,然后对这个点到所有点的距离求和按公式输出就可以了. (这次尝试了用数组模拟链表来做最短路问题,刷新了自己对最短路的理解) 这里构造链表的过程我 ...
- Excel中最精确的计算年龄的公式
身份证算年龄 假设A1是身份证号所在单元格 =IF(MONTH(NOW())<INT(MID(A1,11,2)),INT(YEAR(NOW())-INT(MID(A1,7,4)))-1,IF(M ...
- sql server2005版本中,len函数计算了字符串末尾的空格
sql server2005版本中,len函数计算了字符串末尾的空格的长度,以下是测试脚本: print @@version declare @v varchar(max) set @v = 'hp, ...
- dgraph解决社交关系中的正反向查找
dgraph解决社交关系中的正反向查找 本篇介绍的是, 社交关系中的关注者与被关注者在dgraph中如何实现查找. 对dgraph的基本操作不太清楚的可以看看我之前写的博客 dgraph实现基本操作 ...
- jQuery中height()不能精确计算的问题
jQuery中关于高度的计算有三个方法:outerHeight().innerHeight().height() outerHeight():获取元素集合中第一个元素的当前计算高度值,包括paddin ...
随机推荐
- MySQL-数据库创建与删除
创建数据库 在MySQL中,数据库是用于存储和操作诸如表,数据库视图,触发器,存储过程等数据的对象的集合. 要在MySQL中创建数据库,使用CREATE DATABASE语句,如下: CREATE D ...
- 操作JSON对象
JSON类型对象,最简单了,就是键值对,key:value.key:value.一直不停地key:value下去,层层嵌套,理论上多少层都可以,只要你喜欢. 可是,每次应用JSON,我都心烦意乱,甚至 ...
- mongodb配置复制集replset
Mongodb的replication主要有两种:主从和副本集(replica set).主从的原理和mysql类似,主节点记录在其上的所有操作oplog,从节点定期轮询主节点获取这些操作,然后对自己 ...
- 美国诚实签经验——必带材料:护照,证件照,DS160确认页,面试预约确认页,+境外照片
Step3. 准备签证材料这些材料如果准备,请一定围绕着你的DS160表格,不可说谎,但可适当修饰,辅佐它,烘托它,营造出一种——你绝无可能去不复返,绝无可能制造麻烦,绝无想占人便宜的意思,并且随时可 ...
- CollapsingToolbarLayout Toolbar的title覆盖问题
CollapsingToolbarLayout 里: 1 2 app:titleEnabled="true" app:title="Hello" Toolbar ...
- 推理集 —— death
事故: 自杀: 他杀: 1. 跳楼 头向下死得比较快,没那么痛苦. 脚向下,不会立刻死亡,痛苦至极.死亡原因可能不是跳楼,而是失血过多而死 扑下去, 同头向下. 仰着跌下去,同头向下.. 跳楼最好头先 ...
- gitweb
1. 简介 Gitweb提供了git版本库的图形化web浏览功能.可以到网站http://git.kernel.org/体验下效果,如下图所示. Gitweb界面 它既可以通过配置架设于web服务器上 ...
- 手推FP-growth (频繁模式增长)算法------挖掘频繁项集
一.频繁项集挖掘为什么会出现FP-growth呢? 原因:这得从Apriori算法的原理说起,Apriori会产生大量候选项集(就是连接后产生的),在剪枝时,需要扫描整个数据库(就是给出的数据),通过 ...
- E20180127-hm
retain vt. 保持; 留在心中,记住; 雇用; 付定金保留;
- [转载]android常用的API接口调用
原文地址:android常用的API接口调用作者:宋耀 显示网页: Uri uri = Uri.parse("http://www.google.com"); In ...