Linux内核漏洞精准检测如何做？SCA工具不能只在软件层面

摘要：二进制SCA工具要想更好的辅助安全人员实现安全审计、降低漏洞检测的误报率，必须向更细颗粒度的检测维度发展，而不仅仅停留在开源软件的层面，同时对漏洞库的要求也需要向细颗粒度的精准信息提出的挑战。

本文分享自华为云社区《Linux内核漏洞精准检测》，作者：安全技术猿。

Linux内核结构：

Linux内核由七个部分构成，每个不同的部分又有多个内核模块组成，结构框图如下：

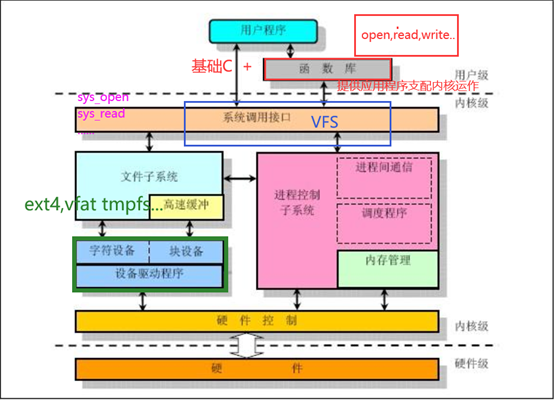
图片引用来自ttps://blog.csdn.net/weixin_44742824/article/details/113814934

Linux裁剪场景分析：

通过分析Linux内核源代码可以看到不同目录中存放着不同模块的实现代码，同时在编译时可以config中配置的信息来控制哪些模块编译到最终的二进制中，哪些模块被裁剪掉，比如以IPV6模块为例，控制该模块的配置名称为CONFIG_IPV6，如果该配置项为设置为y，则表示该功能模块未被编译到最终的二进制文件中，如下所示：

如果该功能模块被裁剪了，即使该漏洞没有被补丁修复，那么该功能模块中存在的漏洞在二进制中也是不受影响的，因此和IPV6相关的漏洞在漏洞检测时就应该在报告中明显的标识出不受该漏洞的影响，如CVE-2013-0343（Linux kernel 3.8之前版本内的net/ipv6/addrconf.c中的函数 ipv6_create_tempaddr没有正确处理IPv6临时地址生成问题，可允许远程攻击者通过 ICMPv6 Router Advertisement (RA) 消息，造成拒绝服务，然后获取敏感信息。）。

业界二进制SCA工具不能检测的原因分析：

为什么目前业界通常的二进制SCA工具无法做到精准检测，原因是因为业界二进制SCA工具是基于检测到的开源软件名称和版本号来关联出已知漏洞清单的，而这种通过裁剪功能模块的方法来应用Linux内核，开源软件名称和版本号是不会改变的，因此工具就无法精准的检测出来了。

二进制SCA工具如何实现该功能：

要实现Linux内核裁剪场景下的已知漏洞精准检测，二进制SCA工具必须在原来检测开源软件名称和版本号的基础上，需要实现更新细颗粒度的检测技术，基于源代码文件颗粒度、函数颗粒度的检测能力，从而实现裁剪场景下已知漏洞的精准检测，即可以知道哪些代码被编译到最终的二进制文件中，哪些代码没有参与编译。同时漏洞库也必须实现对细颗粒维度的支持，即漏洞信息必须精准定位是由哪些文件和函数中的代码片段引入的。

以CVE-2013-0343为例，通过分析漏洞描述信息和Linux内核源代码，可以获取到该漏洞和下面这些位置代码相关的定位信息：

"CVE-2013-0343": {

"net/ipv6/addrconf.c": [

“addrconf_add_ifaddr”,

“addrconf_dad_begin”,

“addrconf_dad_stop”,

“addrconf_dad_work”,

“addrconf_del_ifaddr”,

“addrconf_prefix_rcv”,

“addrconf_verify_rtnl”,

“addrconf_verify_work”,

“inet6_addr_add”,

“inet6_addr_del”,

“inet6_addr_modify”,

“inet6_rtm_deladdr”,

“inet6_rtm_newaddr”,

“inet6_set_iftoken”,

“inet6_set_link_af”,

“ipv6_create_tempaddr”,

“manage_tempaddrs”

]

}

基于如果引入漏洞的源代码没有参与编译出二进制，那么编译出来的二进制也就是不存在该漏洞的原理；因此只要二进制SCA工具能检测出上述位置的源代码没有参与编译出最终的vmlinux二进制文件，那么此vmlinux文件就不受CVE-2013-0343漏洞的影响。

总结：

二进制SCA工具要想更好的辅助安全人员实现安全审计、降低漏洞检测的误报率，必须向更细颗粒度的检测维度发展，而不仅仅停留在开源软件的层面，同时对漏洞库的要求也需要向细颗粒度的精准信息提出的挑战。

文末福利：华为云漏洞扫描服务VSS 基础版限时免费体验>>>

点击关注，第一时间了解华为云新鲜技术~