poj1631Bridging signals(最长单调递增子序列 nlgn)

Bridging signals

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12251		Accepted: 6687

Description

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task? 

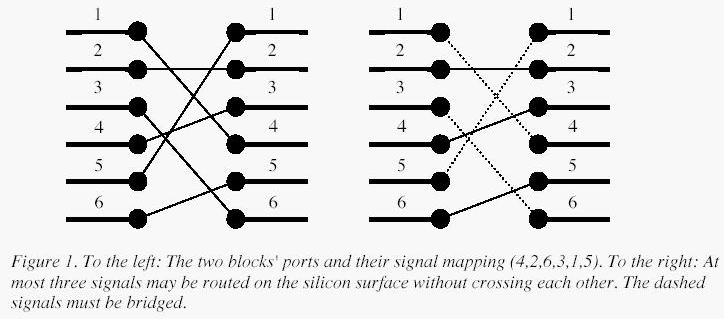
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number specifies which port on the right side should be connected to the i:th port on the left side.Two signals cross if and only if the straight lines connecting the two ports of each pair do.

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

 #include <iostream>
 #include <cstring>
 #include <algorithm>
 #include <cstdio>
 using namespace std;
 const int MAX =  + ;
 int a[MAX],d[MAX];   //a是原始数据，d是递增子序列
 int Find(int c[],int len, int x)
 {
     int l = ,r = len;
     int mid;
     while(l <= r)
     {
         mid = (l + r) / ;
         if(c[mid] == x)
             return mid;
         else if(c[mid] > x)
             r = mid - ;
         else if(c[mid] < x)
             l = mid + ;
     }
     return l;
 }
 int main()
 {
     int t,n,len;
     scanf("%d", &t);
     while(t--)
     {
         scanf("%d", &n);
         for(int i = ; i <= n; i++)
             scanf("%d", &a[i]);
         len = ;
         d[] = a[];
         for(int i = ; i <= n; i++)
         {
             int j = Find(d,len,a[i]);
             d[j] = a[i];
             if(j > len)
                 len = j;
         }
         printf("%d\n",len);
     }
     return ;
 }

二分