PID控制算法

四轴如何起飞的原理

四轴飞行器的螺旋桨与空气发生相对运动，产生了向上的升力，当升力大于四轴的重力时四轴就可以起飞了。

四轴飞行器飞行过程中如何保持水平：

我们先假设一种理想状况：四个电机的转速是完全相同的

是不是我们控制四轴飞行器的四个电机保持同样的转速，当转速超过一个临界点时（升力刚好抵消重力）四轴就可以平稳的飞起来了呢？

答案是否定的，由于四个电机转向相同，四轴会发生旋转。我们控制四轴电机1和电机3同向，电机2电机4反向，刚好抵消反扭矩，巧妙的实现了平衡：

实际上由于电机和螺旋桨本身制造的差异我们无法做到四个电机转速完全相同，如果我们控制同样的转速很有可能飞行器起飞之后就侧翻了。这时候大家可能会想到要用遥控器来控制电机，我们来尝试一下：

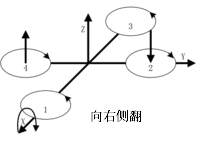
由于电机的不平衡，在人眼的观察下发现飞机向右侧翻，我们控制右侧电机1电机2提高转速增加升力，飞机归于平衡。由于飞机是一个动态系统，在接下来我们会一直重复：

观察->大脑计算->控制->观察->大脑计算->控制这个过程。

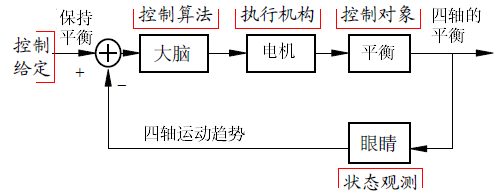
但事实上这是不可能的，因为人无法长时间精确的同时控制四个电机。我们需要一个自动反馈系统替代人操作来完成飞机的自稳定，我们人只需要控制飞机的方向和高度就可以了。这个系统中反馈由姿态传感器替代眼睛，而大脑则由单片机来替代。这时候该PID控制系统出场了！

什么是PID?

PID控制器由偏差的比例（P）、积分（I）和微分（D）来对被控对象进行控制，是应用最为广泛的一种自动控制器。

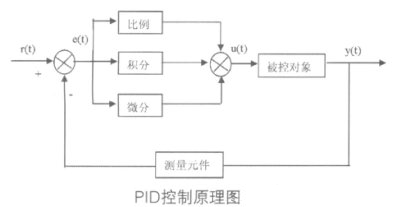
比例（P）控制

比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差（Steady-state error）。

积分（I）控制

在积分控制中，控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统（System with Steady-state Error）。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。积分项输出：

微分（D）控制

微分调节就是偏差值的变化率。使用微分环节能够实现系统的超前控制。如果输入偏差值线性变化，则在调节器输出侧叠加一个恒定的调节量。大部分控制系统不需要调节微分时间。因为只有时间滞后的系统才需要附加这个参数。如果画蛇添足加上这个参数反而会使系统的控制受到影响。微分项输出：

综上所述得到一个一条公式，这个就是模拟PID：

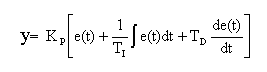
而PID中又可以只使用PI项构成比例-积分控制器，使用PD项构成比例-微分控制器。在Crazepony四轴飞行器中我们使用了增量式PD控制，以ROLL方向角度控制为例：

测得ROLL轴向偏差：

偏差=目标期望角度-传感器实测角度

DIF_ANGLE.X = EXP_ANGLE.X - Q_ANGLE.Roll;

比例项的计算：

比例项输出 = 比例系数P * 偏差

Proportion =  PID_Motor.P * DIF_ANGLE.X;

微分项计算：由于陀螺仪测得的是ROLL轴向旋转角速率，角速率积分就是角度，那么角度微分即角速率，所以微分量刚好是陀螺仪测得的值。

微分输出=微分系数D*角速率

DifferentialCoefficient = PID_Motor.D * DMP_DATA.GYROx;

整合结果总输出为：

ROLL方向总控制量=比例项输出+微分量输出

ROLL 和PIT轴向按照以上公式计算PID输出，但YAW轴比较特殊，因为偏航角法线方向刚好和地球重力平行，这个方向的角度无法由加速度计直接测得，需要增加一个电子罗盘来替代加速度计。如果不使用罗盘的话，我们可以单纯的通过角速度积分来测得偏航角，缺点是由于积分环节中存在积分漂移，偏航角随着时间的推移会偏差越来越大。我们不使用罗盘就没有比例项，只仅使用微分环节来控制。

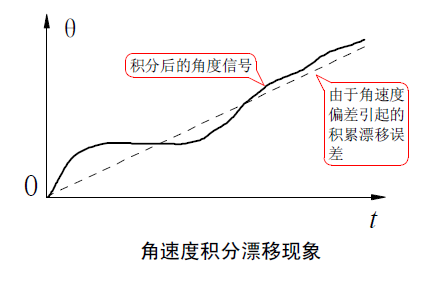
YAW轴输出：

微分输出=微分系数D*角速率

YAW方向控制量 = PID_YAW.D * DMP_DATA.GYROz;

电机的输出：油门控制Throttle是电机输出的基准值，增加油门即可提高四轴高度。最后整合ROLL/PIT/YAW三轴输出量进行电机控制：

Motor[2] = (int16_t)(Thr - Pitch - Roll - Yaw );    //M3

Motor[0] = (int16_t)(Thr + Pitch + Roll - Yaw );    //M1

Motor[3] = (int16_t)(Thr - Pitch + Roll + Yaw );    //M4

Motor[1] = (int16_t)(Thr + Pitch - Roll + Yaw );    //M2

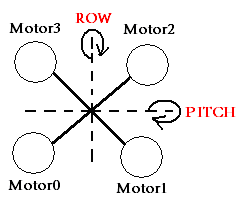
如图四轴绕ROW轴向右下倾斜5度，那么电机1电机2应该提高升力，电机3电机0减小升力恢复平衡状态，所以有以下规则：

Roll方向旋转，则电机1电机2同侧出力，电机0电机3反向出力
Pitch方向旋转，则电机2电机3同侧出力，电机0电机1反向出力
Yaw方向旋转，则电机1电机3同侧出力，电机0电机2反向出力

来源： <http://www.crazepony.com/wiki/algorithm-pid.html>

来自为知笔记(Wiz)