[Luogu P3119] [USACO15JAN]草鉴定Grass Cownoisseur (缩点+图上DP)

题面

传送门：https://www.luogu.org/problemnew/show/P3119

---

Solution

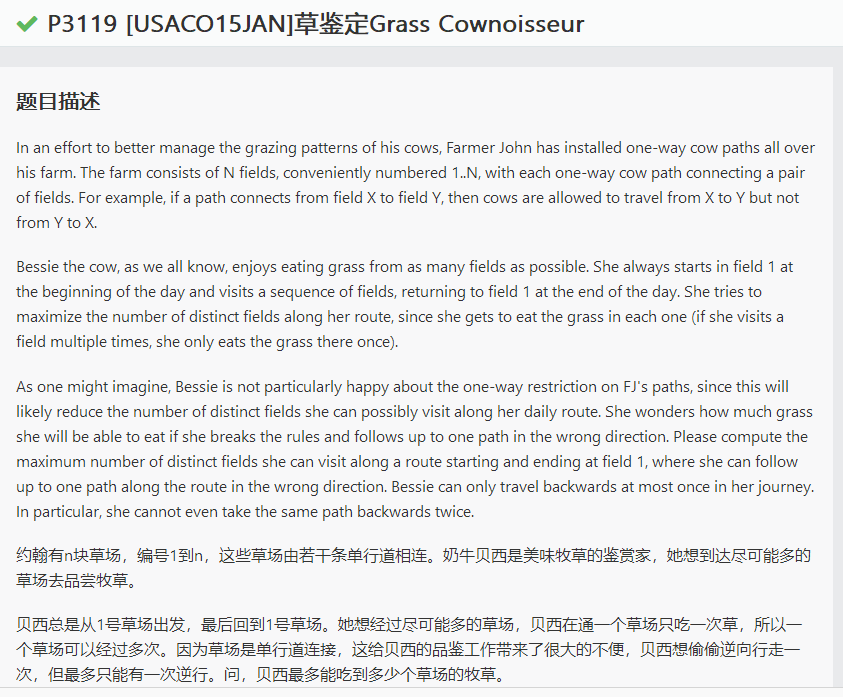
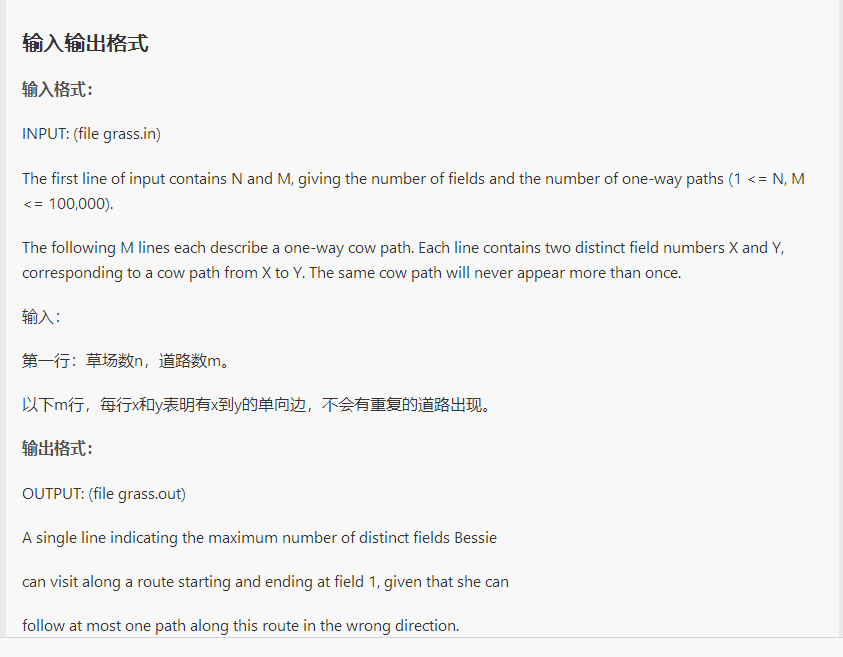
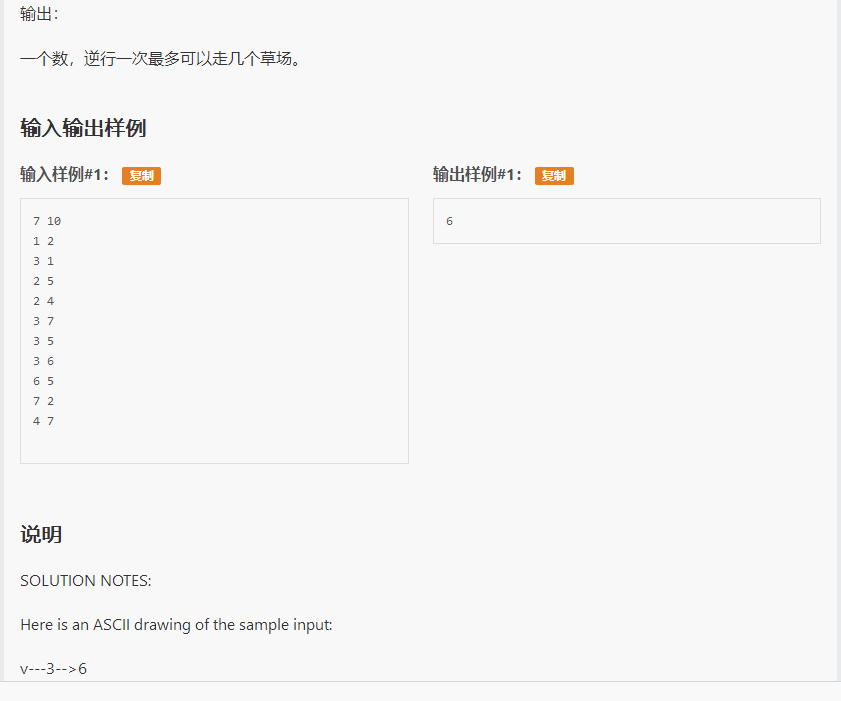
这题显然要先把缩点做了。

然后我们就可以考虑如何处理走反向边的问题。

像我这样的蒟蒻，当然是使用搜索，带记忆化的那种（滑稽）。

考虑设f(i,j)表示到达第i个点，还能走j次反向边，所能到达的最多的点的数量。

转移可以表示为：

如果x能到达1所在的强连通分量或max出来的值不为0，说明当前状态可行，否则不可行。

然后用记忆化搜索表达出来就OK了

---

Code

#include<iostream>
#include<cstdio>
#include<vector>
#include<stack>
#include<cstring>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=100000+100;
struct road
{
    int to,IsBack;
    road (int A,int B)
    {
        to=A,IsBack=B;
    }
};
vector <int> e[N];
vector <road> e2[N];
int belong[N],nd_tot,nd_to,low[N],dfn[N],InStack[N],cnt[N];
stack <int> st;
void Tarjan(int now)
{
    low[now]=dfn[now]=++nd_to;
    InStack[now]=true;
    st.push(now);
    for(int i=0;i<int(e[now].size());i++)
        if(dfn[e[now][i]]==0)
        {
            Tarjan(e[now][i]);
            low[now]=min(low[now],low[e[now][i]]);
        }
        else if(InStack[e[now][i]]==true)
            low[now]=min(low[now],low[e[now][i]]);
    if(low[now]==dfn[now])
    {
        nd_tot++;
        while(st.empty()==false)
        {
            int temp=st.top();
            st.pop();
            belong[temp]=nd_tot;
            InStack[temp]=false;
            cnt[nd_tot]++;
            if(temp==now)
                break;
        }
    }
}
int n,m,S,f[N][2];
int dfs(int now,int back)
{
    if(f[now][back]>=0) return f[now][back];
    int t_ans=0;
    bool OK=false;
    for(int i=0;i<int(e2[now].size());i++)
        if(e2[now][i].to!=S and back-e2[now][i].IsBack>=0)
            t_ans=max(t_ans,dfs(e2[now][i].to,back-e2[now][i].IsBack));
        else if(back>=e2[now][i].IsBack)
            OK=true;
    if(t_ans!=0 or OK==true)
        return f[now][back]=t_ans+cnt[now];
    else
        return f[now][back]=0;
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        e[i].reserve(4),
        e2[i].reserve(4);
    for(int i=1;i<=m;i++)
    {
        int s=read(),t=read();
        e[s].push_back(t);
    }

    for(int i=1;i<=n;i++)
        if(dfn[i]==0)
            Tarjan(i);
    S=belong[1];
    for(int i=1;i<=n;i++)
        for(int j=0;j<int(e[i].size());j++)
            if(belong[i]!=belong[e[i][j]])
            {
                e2[belong[i]].push_back(road(belong[e[i][j]],0));
                e2[belong[e[i][j]]].push_back(road(belong[i],1));
            }

    memset(f,0x80,sizeof f);
    int ans=0;
    for(int i=0;i<int(e2[S].size());i++)
        ans=max(ans,dfs(e2[S][i].to,1-e2[S][i].IsBack));

    printf("%d",ans+cnt[S]);
    return 0;
}

C++（正解）