一文详解滑动平均法、滑动平均模型法（Moving average，MA）

任何关于算法、编程、AI行业知识或博客内容的问题，可以随时扫码关注公众号「图灵的猫」，加入”学习小组“，沙雕博主在线答疑~此外，公众号内还有更多AI、算法、编程和大数据知识分享，以及免费的SSR节点和学习资料。其他平台（知乎/B站）也是同名「图灵的猫」，不要迷路哦~

​

​

什么是移动平均法?

　　移动平均法是用一组最近的实际数据值来预测未来一期或几期内公司产品的需求量、公司产能等的一种常用方法。移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降，且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，是非常有用的。移动平均法根据预测时使用的各元素的权重不同

　　移动平均法是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。因此，当时间序列的数值由于受周期变动和随机波动的影响，起伏较大，不易显示出事件的发展趋势时，使用移动平均法可以消除这些因素的影响，显示出事件的发展方向与趋势（即趋势线），然后依趋势线分析预测序列的长期趋势。

　　移动平均法的种类

　　移动平均法可以分为：简单移动平均和加权移动平均。

　　一、简单移动平均法

　　简单移动平均的各元素的权重都相等。简单的移动平均的计算公式如下： Ft＝（At-1＋At-2＋At-3＋…＋At-n）/n式中，

　　·Ft–对下一期的预测值；

　　·n–移动平均的时期个数；

　　·At-1–前期实际值；

　　·At-2，At-3和At-n分别表示前两期、前三期直至前n期的实际值。 
　　

　　二、加权移动平均法

　　加权移动平均给固定跨越期限内的每个变量值以不同的权重。其原理是：历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以n为周期的周期性变化外，远离目标期的变量值的影响力相对较低，故应给予较低的权重。加权移动平均法的计算公式如下：

　　Ft＝w1At-1＋w2At-2＋w3At-3＋…＋wnAt-n式中，

　　·w1–第t-1期实际销售额的权重；

　　·w2–第t-2期实际销售额的权重；

　　·wn–第t-n期实际销售额的权

　　·n–预测的时期数；w1＋ w2＋…＋ wn＝1

　　在运用加权平均法时，权重的选择是一个应该注意的问题。经验法和试算法是选择权重的最简单的方法。一般而言，最近期的数据最能预示未来的情况，因而权重应大些。例如，根据前一个月的利润和生产能力比起根据前几个月能更好的估测下个月的利润和生产能力。但是，如果数据是季节性的，则权重也应是季节性的。

　　移动平均法的优缺点

　　使用移动平均法进行预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下问题：

　　1、加大移动平均法的期数（即加大n值）会使平滑波动效果更好，但会使预测值对数据实际变动更不敏感；

　　2、移动平均值并不能总是很好地反映出趋势。由于是平均值，预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动；

　　3、移动平均法要由大量的过去数据的记录。

　　移动平均法案例分析 
　　 
　　简单移动平均法在房地产中的运用 
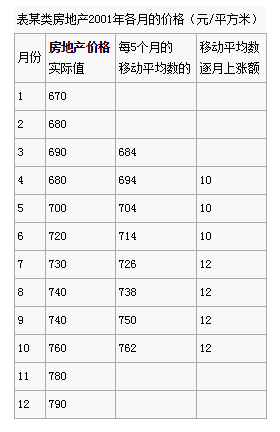
某类房地产2001年各月的价格如下表中第二列所示。由于各月的价格受某些不确定因素的影响，时高时低，变动较大。如果不予分析，不易显现其发展趋势。如果把每几个月的价格加起来计算其移动平均数，建立一个移动平均数时间序列，就可以从平滑的发展趋势中明显地看出其发展变动的方向和程度，进而可以预测未来的价格。

　　在计算移动平均数时，每次应采用几个月来计算，需要根据时间序列的序数和变动周期来决定。如果序数多，变动周期长，则可以采用每6个月甚至每12个月来计算；反之，可以采用每2个月或每5个月来计算。对本例房地产2001年的价格，采用每5个月的实际值计算其移动平均数。计算方法是：把1～5月的价格加起来除以5得684元/平方米，把2～6月的价格加起来除以5得694元/平方米，把3～7月的价格加起来除以5得704元/平方米，依此类推，见表中第三列。再根据每5个月的移动平均数计算其逐月的上涨额，见表中第四列。 
　　​

假如需要预测该类房地产2002年1月的价格，则计算方法如下：由于最后一个移动平均数762与2002年1月相差3个月，所以预测该类房地产2002年1月的价格为：762 ＋ 12 × 3 =798（元/平方米）

ARMA

自回归滑动平均模型（ARMA 模型，Auto-Regressive and Moving Average Model）是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。
ARMA模型(auto regressive moving average model)自回归滑动平均模型，模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法，适用于很大一类实际问题。它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。ARMA模型参数估计的方法很多：
如果模型的输入序列{u(n)}与输出序列{a(n)}均能被测量时，则可以用最小二乘法估计其模型参数，这种估计是线性估计，模型参数能以足够的精度估计出来；
许多谱估计中，仅能得到模型的输出序列{x(n）}，这时，参数估计是非线性的，难以求得ARMA模型参数的准确估值。从理论上推出了一些ARMA模型参数的最佳估计方法，但它们存在计算量大和不能保证收敛的缺点。因此工程上提出次最佳方法，即分别估计AR和MA参数，而不像最佳参数估计中那样同时估计AR和MA参数，从而使计算量大大减少。

 

ARMA模型分为以下三种：

自回归模型（AR：Auto-regressive）

如果时间序列

 ​ 

满足​

其中​是独立同分布的随机变量序列，且满足

​

以及 E( ​ ) = 0则称时间序列为服从p阶的自回归模型。

自回归模型的平稳条件：滞后算子多项式

​

的根均在单位圆外，即φ(B) = 0的根大于1。

移动平均模型（MA：Moving-Average）

如果时间序列 ​ 满足​

，则称时间序列​ 
为服从q阶移动平均模型；移动平均模型平稳条件：任何条件下都平稳。

 

自回归滑动平均模型（ARMA）

如果时间序列 ​ 满足：
​

则称时间序列

 ​

为服从(p,q)阶自回归滑动平均混合模型。或者记为φ(B)

​

= θ(B)

​

>>>关于作者

CSDN 博客专家，2019-CSDN百大博主，计算机（机器学习方向）博士在读，业余Kaggle选手，有过美团、腾讯算法工程师经历，目前就职于Amazon AI lab。喜爱分享和知识整合。

关注微信公众号，点击“学习资料”菜单即可获取算法、编程资源以及教学视频，还有免费SSR节点相送哦。其他平台（微信/知乎/B站），欢迎关注同名公众号「图灵的猫」~