二项分布。计算binomial(100,50,0.25)将会产生的递归调用次数(算法第四版1.1.27)
算法第四版35页问题1.1.27,估计用一下代码计算binomial(100,50,0.25)将会产生的递归调用次数:
public static double binomial(int n,int k,double p){
if(n == 0 && k == 0) return 1.0;
if(n<0 || k<0) return 0.0;
return (1.0-p)*binomial(n-1,k,p) +p*binomial(n-1,k-1,p)
}
虽然书上只让估计调用次数,但是觉得想知道到底调用了几次。
我用图画出递归调用的情况
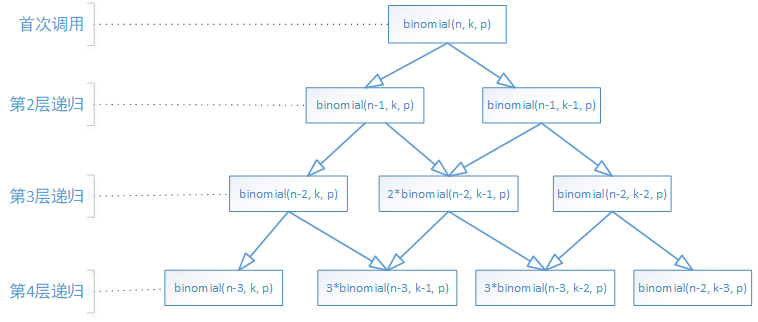
可以看出递归中有很多重复调用比如,第4层递归 分别调用了binomial(n-3,k-1,p)和binomial(n-3,k-2,p)三次。这就是这个算法效率低的原因。可以看出重复调用的次数是一个杨辉三角。
根据杨辉三角的性质,
第m层递归函数被调用的情况为:
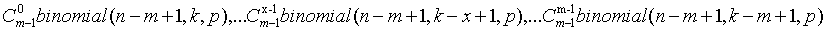
第m层第x(x<=m)项为:

但是有些调用实际上不会发生,结合函数的返回条件:
if(n == 0 && k == 0) return 1.0;
if(n<0 || k<0) return 0.0;
设我们传入的初始参数为n=N,k=K 则,可以得出已下结论:
- 当m=N+1且x=K+1时,满足程序退出的第一个条件;
- 当m>N+1或x>K+1时,满足程序退出的第二个条件(根据杨辉三角的性质,第m行有m项,所有此时有K+1<x<=m)
让我们看看满足以上结论的详细项:
1.下列递归调用的x>K+1,满足结论2:
- m=K+2行的第K+2项:
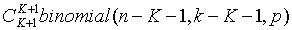
- m=K+3行的第K+2项到K+3项:
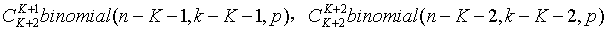
- ……
- m=N+1行的第K+2项到最后一项:
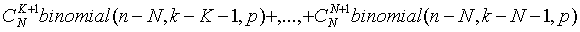
- m=K+2行的第K+2项:
2.m=N+1行的第K+1项递归调用的第一个参数n和第二个参数k均为0,满足结论1。
3.当m=N+2时,显然m>N+1,满足结论2;
如果调用 参数满足函数退出条件,那么由
参数满足函数退出条件,那么由 调用的递归实际上就不会发生,数量为
调用的递归实际上就不会发生,数量为 的系数✖️2。
的系数✖️2。
N+2之后的递归都不会发生,所以做计算时只考虑到N+2层。N+2层的无效调用数量,为N+1层满足结论1或2的调用的数量*2,一次类推,直到K+3层的无效调用数量,为K+2层满足结论1或2的调用数量*2;K+2层到1层上,所有调用都有效;因为K+1层到1层,没有调用满足结论1或2.
根据杨辉三角的性质:从第1层到第N+2层所有的系数和为 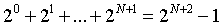
其中不会实际发生的调用次数为从(K+2层到N+1层):
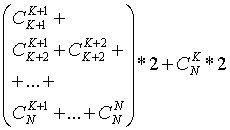
化简之后为:
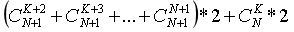
再次化简
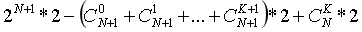
所以最后程序递归调用的总次数为
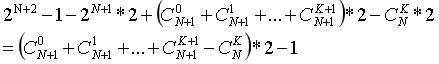
运行随机验证几个组合,可以证明上述公式是正确的!
二项分布。计算binomial(100,50,0.25)将会产生的递归调用次数(算法第四版1.1.27)的更多相关文章
- 计算阶乘n!末尾0的个数
一.问题描述 给定一个正整数n,请计算n的阶乘n!末尾所含有“0”的个数.例如: 5!=120,其末尾所含有的“0”的个数为1: 10!= 3628800,其末尾所含有的“0”的个数为2: 20!= ...
- python_计算1+……+100中偶数和
如何计算1+--+100中偶数和? 1. 把奇数去掉,通过if,判断累加数除以2的余数,是否为1,判断是否是奇数 2. 通过continue 跳过对奇数的累加 #!/usr/bin/python3 d ...
- MathExam小学一二年级计算题生成器V1.0
MathExam小学一二年级计算题生成器v1.0 一.预估与实际 PSP2.1 Personal Software Process Stages 预估耗时(分钟) 实际耗时(分钟) Planning ...
- pat1067. Sort with Swap(0,*) (25)
1067. Sort with Swap(0,*) (25) 时间限制 150 ms 内存限制 65536 kB 代码长度限制 16000 B 判题程序 Standard 作者 CHEN, Yue G ...
- Hadoop 系统配置 map 100% reduce 0%
之前在本地配置了hadoop伪分布模式,hdfs用起来没问题,mapreduce的单机模式也没问题. 今天写了个程序,想在伪分布式上跑一下mapreduce,结果出现 map 100% reduce ...
- 【男性身材计算】胸围=身高*0.48(如:身高175cm的标准胸围=175cm*0.61=84cm);腰围=身高*0.47(如:身高175c… - 李峥 - 价值中国网
[男性身材计算]胸围=身高*0.48(如:身高175cm的标准胸围=175cm*0.61=84cm):腰围=身高*0.47(如:身高175c- - 李峥 - 价值中国网 李峥:[男性身材计算]胸围=身 ...
- resin4.0.25 安装配置 及结合eclipse开发
resin4.0.25 安装配置 及结合eclipse开发 本文大部分内容是对官网的翻译,及自己配置后的一些体会. 一. 基于win ,resin基本安装1,安装jdk1.6或更高版本2,配置环境 ...
- linux系统更新rpm包问题 ,报错rhn-check-2.0.2-5.el7.noarch has missing requires of yum-rhn-plugin >= ('0', '1.6.4', '1')
报错信息: rhn-check-2.0.2-5.el7.noarch has missing requires of yum-rhn-plugin >= ('0', '1.6.4', '1') ...
- wordcount程序出现map 100% reduce 0%问题的解决方法
运行wordcount程序一直停在map 100% reduce 0%, input文件夹的内容: 其中: f1.txt中的内容为:hello hadoop f2.txt中的内容为:hello had ...
随机推荐
- 李洪强iOS开发之苹果企业开发者账号申请流程
李洪强iOS开发之苹果企业开发者账号申请流程 一. 开发者账号类型选择 邓白氏码 DUNS number,是Data Universal Numbering System的缩写,是一个独一无二的9位数 ...
- Linux(Ubuntu/Debian/CentOS/RedHat)下交叉编译boost库
我用的软件版本如下(其他版本编译方法与此完全相同): Boost Ver: 1.55.0Compiler : GNU gcc 4.6 for ARM 1. 确保ARM编译成功安装,并配置好环境变量.2 ...
- nyoj16矩形嵌套(第一道dp关于dag的题目)
http://acm.nyist.net/JudgeOnline/problem.php?pid=16 题意:有n个矩形,每个矩形可以用a,b来描述,表示长和宽.矩形X(a,b)可以嵌套在矩形Y(c, ...
- win7如何连接蓝牙键盘
控制面板->硬件和声音->查看设备和打印机->添加设备
- WP架构设计(一)MVVM回顾
[MVVM的定义] MVVM的目的是什么? 简单总结起来一句话:分离UI逻辑和业务逻辑.这一点和被大家熟知的MVP和MVC是一致的. 下面详细来说明下这个问题,下面一段英文来自Msdn ...
- SenCha Touch HTML 5 应用程序缓存
http://www.cnblogs.com/qidian10/p/3292876.html https://developer.mozilla.org/zh-CN/docs/HTML/Using_t ...
- asp.net 简单分页打印
<html> <head> <title>看看</title> <meta http-equiv="Content-Type" ...
- 深度剖析java编码,彻底解决java乱码问题_1
理解: 1,Java编译器(即编译成class文件时) 用的是unicode字符集. 2,乱码主要是由于不同的字符集相互转换导致的,理论上各个字符的编码规则是不同的,是不能相互转换的,所以根本解决乱码 ...
- 对session的操作
request.getSession().removeAttribute("amount");request.getSession().setAttribute("amo ...
- connect() failed (111: Connection refused) while connecting to upstream, cli
php-fpm没有运行 执行如下命令查看是否启动了php-fpm,如果没有则启动你的php-fpm即可 netstat -ant | grep 9000 没有运行为空,有运行显示 tcp 0 0 12 ...
