android 多线程概述

android多线程，一直是一个麻烦的事情，要掌握它的本质，我们需要搞清楚一个问题，linux多线程的本质。

我们这篇文章，来讨论以下的议程：

了解linux的历程，了解android的异步任务机制，了解android的多步任务。

说到linux的多线程，我们要比较windows与linux的多线程的模型。

windows线程———线程与进程多对多模型，线程的调度都在核内。

操作系统——操作系统在的视线系统，部分linux的线程是一对一，一对多的模式，线程调度在核外。

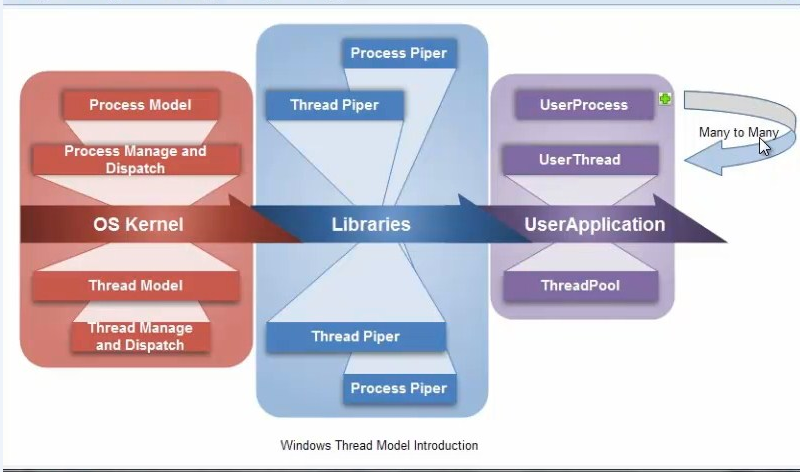
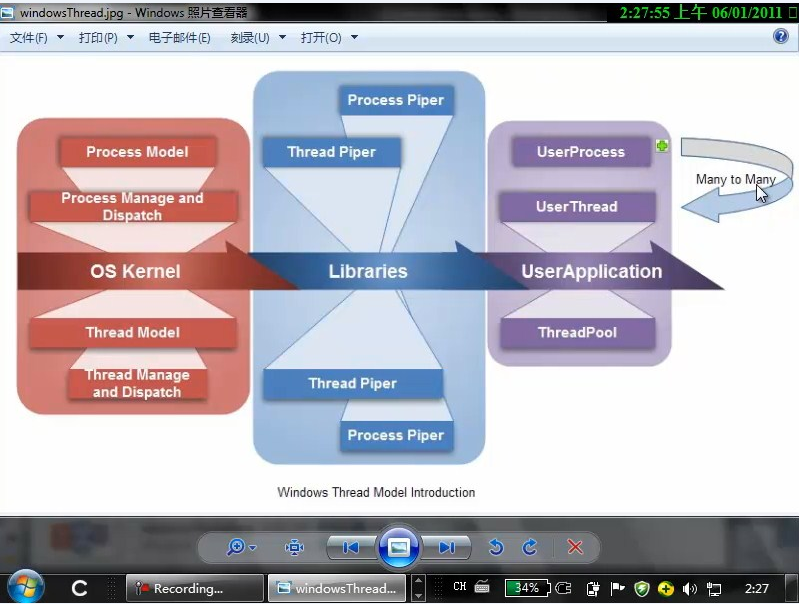
这是windows进程，windows进程的模型如下：

通过这张图，我们能够精确的看到在kernel中，windows已经定义了一些进程管理类和线程的模型，在类库的层面，你只需要来打通这个线程进程的管道，儿在用户层我们只需要尽情的使用线程池的线程。

对于linux的线程的知识，我们知道的linux的设计的王道，就是一个简略既是美的原则，利纳科斯没有考虑多线程的。他的进程，线程的示意图如下：

我们可以看到这个linux没有所谓的线0程管理，只有一个轻量级的线程管理，所谓轻量级的线程的管理，只不过是为减少进程的间切花，实现线程中资源的共享。linux的进程只能够在类库的层面来实现了，因此linux的进程与线程的定义是一对一的作用。

总而言之言而总之，linux的进程是用户态实现的，windows的进程是内核态的实现的。

对于linux的进程与windows的进程，我们能够通过一个手中模行来实现，windows就好比，动手指头是神经系统（内核）控制的，高效，资源开销少，linux动手指头是外人（用户）控制的，低效，资源少。

有了这个分析，预知android的多线程的知识，请听下回分解。

好好学习，天天向上。