RSA，Miller-Rabin素数测试的源流及其证明

一、RSA与公钥加密系统的起源与影响。

为了更好地突出公钥加密系统相对私钥加密系统的优势，让我们从这两个问题开始：

这个世界上如果没有公钥加密系统会怎么样呢？全用私钥加密系统会出现什么问题呢？

首先，私钥密码系统中的密码，加密解密之间是存在共享性的，也就是说，会加密就能做到会解密，会解密也就能做到会加密。

如果私钥密码系统用来做数字签名，会发生什么呢？你只要告诉了别人验证你的数字签名的正确性方法（解密），就同时告诉了他们伪造这个数字签名的方法（加密）。瞬间爆炸Orz。

其次，私钥加密系统需要有一次绝对保密的初始化过程。双方需要保密地交流一次约定加密方式。

在以往，这个过程都通过线下保证了保密。比如特工在出发前就跟总部约定好加密方式。

互联网时代这就出现问题了。如果你开了一个网站，需要跟每个用户进行保密交流。你很难跟每个用户都线下碰次头约定一下加密问题。可是如果交流全在网络上进行的话，双方约定加密方式的那几条信息本身用啥来加密呢。。。这就很尴尬了(ಡωಡ)

1977年，罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）（膜一发图灵奖Orz）将大数因式分解的不对称性与对密码系统不对称性的需求联系起来，创造了第一个公钥加密系统，RSA算法。迄今为止，2048位的RSA秘钥仍是非常安全的，在全世界被广泛使用。

（这种关联的能力或许就是创造力的核心源泉之一吧，我想，RSA如同蒙拉丽莎的微笑，“独钓寒江雪”的意境，都是人类巅峰创造力的结晶）

二、RSA的分析。

先直接奉上RSA加密流程

找两个不相同的素数p,q.设n=pq

取d,e使de=1+k(p-1)(q-1)成立

对于原文M（一个01串），加密方式为C=M^e mod n，C即为密文

解密方式为 N=C^d mod n

最后有 N ≡ M mod n

实际操作时n公开，e，d公开一个， q,p保密

正确性证明

N=C^d=M^ed=M^(1+k(p-1)(q-1))=M*M^k(p-1)(q-1)

因为p,q都是素数，由费马小定理：M^(p-1)≡1 (mod p) ,M^(q-1)≡1 （mod p）

得C≡M（mod p）

费马小定理是欧拉定理的特例，考虑到后面的需要，在这里直接证明欧拉定理及欧拉函数的一些性质：

另外由于d，e是对称的，d可以用来解密e发来的消息也可以用来加密只给e看的消息。

即加密方式C也可以为C=M^d mod n,解密方式为 N=C^e mod n

三、密钥的生成

怎么找到一个足够大的素数呢？

我自己的第一反应是筛法。。可是马上意识到如果能从遍历找q,p就能遍历破p，q。其次如果要遍历找高达2048位的素数即使计算机运算速度亿亿次每秒，也足够算到地老天荒。（粗略估算了下结果是个高达几百位的数字，单位年）

从而遍历的办法是肯定不行的。但联想欧拉函数在n充分大的时候趋近于n/lnn（即n非常大的时候小于n的素数个数大约为n/lnn,该命题已被证明但我不会证），我们可以知道2048位的数中素数的密度并不算很小，几千分之一的样子。

如果有一个算法可以判断出一个数是不是素数，再猜个几千次，我们就能得到想要的2048位的素数了。

于是引出另一个神奇的算法:Miller-Rabin算法（又出现了一个图灵奖的名字Orz）

Miller-Rabin算法的思想起源于对费马小定理的逆定理的研究。

费马小定理说，对一个素数p，对任意的小于p并大于1的自然数a有a^p-1≡1 mod p。

那么如果一个数不满足上述性质，那它肯定是合数。并且绝大部分合数甚至只用a=2做判断便可以让其现形，在小于10000的数中，只有22个合数能逃过以2为底的判断（即只有22个数满足2^n-1≡1 mod n，且n是合数）。这些数被称为基于2的伪素数（Fermat pseudoprime to base a）。以此类推还有以a=3为底的为素数，以n为底的伪素数。

看上去似乎费马小定理的逆定理是成立的，如果选取足够多的底，或许没有合数可以逃过判断。

但很遗憾的，并不是。1729 = 7×13×19就可以逃过所有判断，而它是合数。此外还有561,2465等（它们被统称为carmichael number）

这个最初的思想叫做费马素性检验，米勒（Miller）和拉宾（Rabin）改进了它，创造出了更加具有实用性的Miller-Rabin算法。

该算法源于这样一个结论，对于一个奇素数p，令p-1=2^tu,其中t>=1且u是奇数。对i=0,1,2. t

　　　　　　　　　　　　　　　

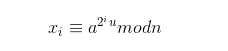
xi形成的序列{x0,x1,..,xt}必为{1,1,1，    ，1}或{x,y,z,____,-1,1,1,1,1}

原因很简单，如果p是素数，一个数mod p余1，那把它开平方自然有余1或-1.

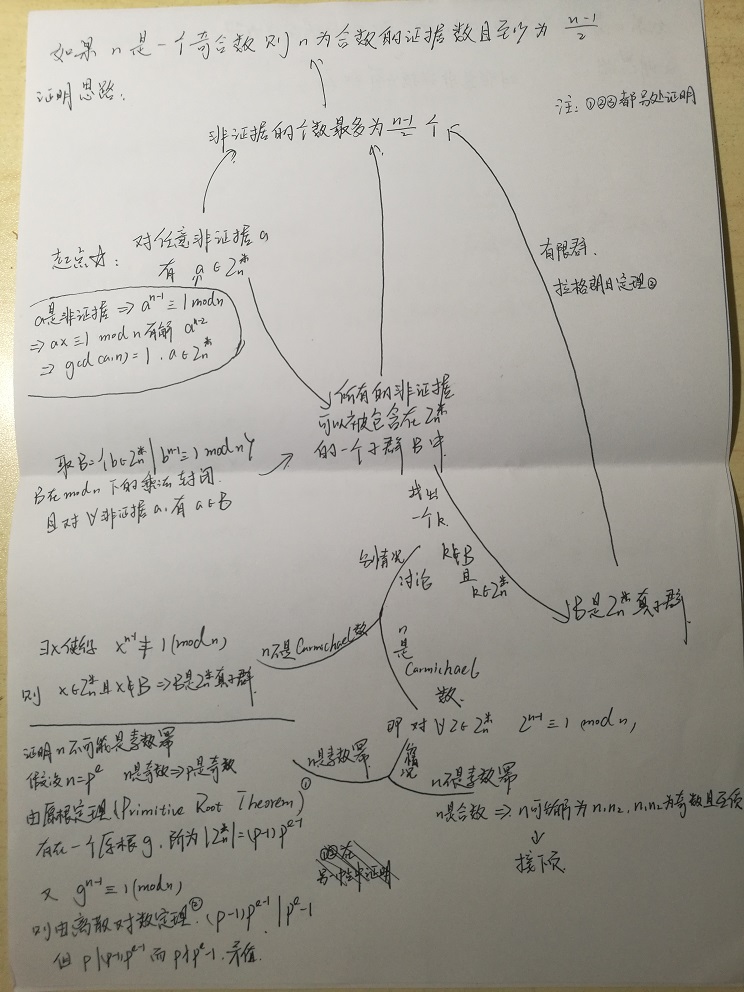
以下证明Miller-Rabin测试对任何一个奇合数都能找到至少（n-1）/2个a使得生成的序列不满足上述结论（称这样的a为证据），包括carmichael number。

（参考文献：算法导论）

在实际测试中，并不会找出所有比待测数小的数字进行测试。因为2048位的整数实在太大了。但如果选取s个数进行测试，出错的概率至多为2^-s。（即待测数明明是个合数，却测出来是个素数）。选1万个数测试就非常保险了。

综上，在寻找RSA密钥的过程中，利用素数密度为lnn/n的特点，知道了2048位整数中选几万奇数就极可能其中有素数。对这些数分别进行素数测试，如果选一万个数测试，每个数的出错概率为2的一万次幂分之一。几万个数总的出错概率非常非常低。于是找到了相当靠谱的2048位素数。

实际应用中似乎还有一些技巧用来使生成的素数更保险。但这不在我这篇文章的讨论范围里了。

以上。