[西安交大附中集训] d6 删边(cip)

B. 删边(cip.cpp/in/out 1S/256M)

题面

给出一个没有重边和自环的无向图，现在要求删除其中两条边，使得图仍然保持连通。

你的任务是计算有多少组不合法的选边方案。注意方案是无序二元组。

输入格式

第一行是两个整数 N 和 M，分别表示顶点数和边数

接下来 M 行，每行 2 个整数，表示一条无向边

输出格式

输出一行，表示对应的答案

输入样例

5 6

1 2

2 3

1 3

3 4

4 5

3 5

输出样例

6

数据规模

测试点 N M

10% 3000 7000

70% 50000 100000

100% 100000 300000

题解

首先，如果一条边是桥，那么另一条边任意；

对于非桥边：

构建DFS树。

显然，只有两种组合：树边+树边，树边+返祖边。

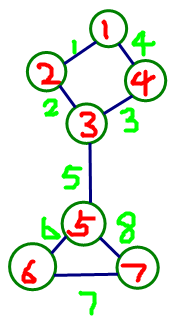
对每一条树边记录跨过它的返祖边集合 \(S\) ，返祖边跨过它的集合仅有它本身。

我们就会发现，任意两条非桥边同时删去可以使图不连通的充要条件是跨过他们的返祖边集合相同。

证明显然。

然后考虑如何表示一条边的返祖边集合：

利用哈希，给每条返祖边一个随机权值，加入哈希集合。

把边权变为点权。因为每条边有两个端点，考虑异或，给边的两个端点赋上这条边的权值。

树形dp，每个点异或它的所有儿子的权值，这样某条返祖边未覆盖的点就不会受到它的影响。将每个点的权值加入hash集合，表示这个点到它父亲的边。

哈希值有两种情况：

1. hash==0 此时这条边为桥，ans+=边数；
2. hash!=0 求出每种哈希值的出现次数 \(m\) ，ans+=m*(m-1)/2。

\(ans\) 即为答案。

ps1： 这样似乎可以推广到割k条边？

ps2： tarjan可以省了？

代码

放一下std：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<queue>
#include<set>
#define SF scanf
#define PF printf
#define mp make_pair
#define fir first
#define sec second
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int MAXN = 100000;
const int MAXM = 300000;
struct Node {
	int v, next;
} Edge[MAXM*2+10];
int adj[MAXN+10], ecnt, n, m;
LL Hash[MAXN+10], ans;
bool vis[MAXN+10];
vector <pii> not_tree_edges;
vector <LL> Hash_set;
void addedge(int u, int v) {
	Node &e = Edge[++ecnt];
	e.v = v; e.next = adj[u]; adj[u] = ecnt;
}
void add(int u, int v) {
	addedge(u, v); addedge(v, u);
}
void dfs(int u, int fa) {
	vis[u] = true;
	for(int i = adj[u]; i; i = Edge[i].next) {
		int v = Edge[i].v;
		if(!vis[v]) dfs(v, u);
		else if(v != fa && v < u) not_tree_edges.push_back(make_pair(v, u));
	}
}
LL Rand() {
	LL x = 0;
	for(int i = 0; i < 3; i++)
		x = (x << 16) | rand();
	return x;
}
void make_Hash() {
	for(int i = 0; i < not_tree_edges.size(); i++) {
		LL sta = Rand();
		Hash[not_tree_edges[i].fir] ^= sta;
		Hash[not_tree_edges[i].sec] ^= sta;
		Hash_set.push_back(sta);
	}
}
LL calc(int u) {
	vis[u] = true;
	for(int i = adj[u]; i; i = Edge[i].next) {
		if(vis[Edge[i].v]) continue;
		LL val = calc(Edge[i].v);
		Hash[u] ^= val;
		Hash_set.push_back(val);
	}
	return Hash[u];
}
void count_ans() {
	sort(Hash_set.begin(), Hash_set.end());
	int cnt = 0;
	for(int i = 0; i < Hash_set.size(); i++)
		if(!Hash_set[i])
			cnt++;
	ans += 1LL * cnt * (m - cnt);
	for(int i = 0, j = 0; i < m; i = j) {
		while(j < m && Hash_set[i] == Hash_set[j]) j++;
		int del = j - i;
		ans += 1LL * del * (del - 1) / 2;
	}
}
int main() {
	srand(19981103);
	SF("%d%d", &n, &m);
	for(int i = 1; i <= m; i++) {
		int u, v;
		SF("%d%d", &u, &v);
		add(u, v);
	}
	dfs(1, 0);
	memset(vis, 0, sizeof(vis));
	make_Hash();
	calc(1);
	count_ans();
	cout << ans;
}