【2016北京集训测试赛（十六）】 River （最大流）

Description

　　　　　　　　　　　　　　　　　　　　  Special Judge

Hint

　　注意是全程不能经过两个相同的景点，并且一天的开始和结束不能用同样的交通方式。

---

题解

　　题目大意：给定两组点，每组有$n$个点，有若干条跨组的有色无向边。求一种方案，包括若干个不相交的连通块，覆盖全部点，每个连通块满足能一笔画（不经过重复的点）并且相邻两次经过的边颜色不相同（开头和结尾经过的边也不能相同）。

　　是不是有点类似二分图匹配的问题呢？我们还是考虑用最大流来建图。

　　一笔画的时候，每一个经过的点有且只有一条入边，有且只有一条出边，即度数必须为2；两条边的颜色还不能相同。每一个点都如下图所示：

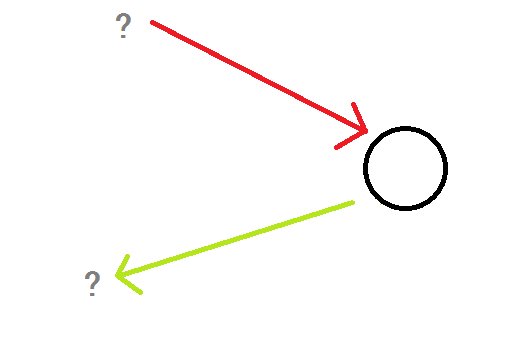
　　事实上，我们并不用考虑经过的每一条边的方向！这并不是我们决策的关键，只要最后回到起点即可，如下图所示。

　　

　　

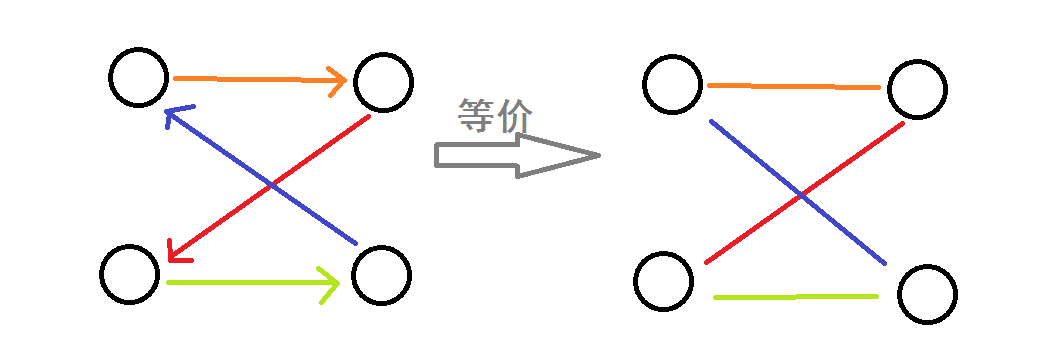
建图

　　怎么用最大流来限制这两个条件呢？

　　先上效果图：

　　

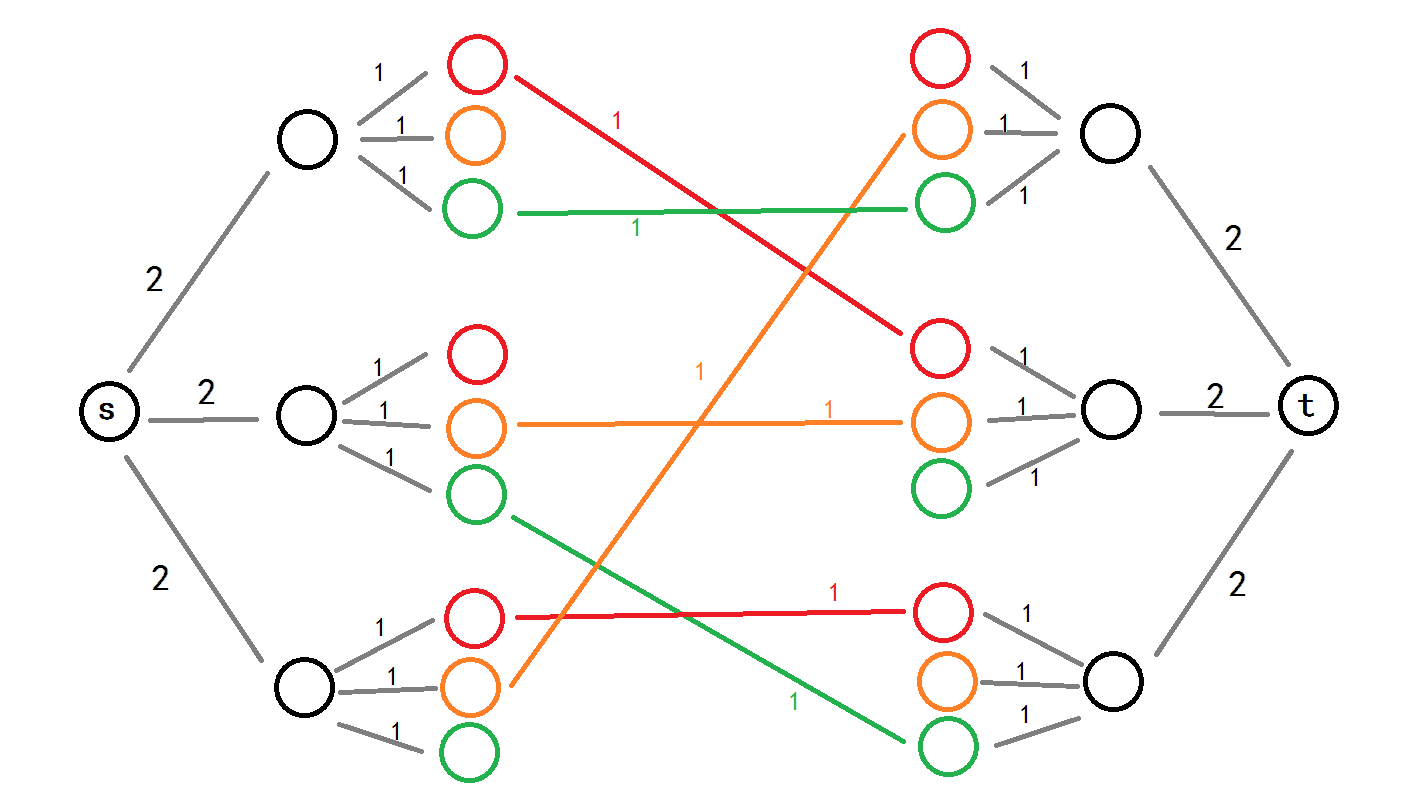
　　对于度数为2，考虑用一条容量为2的边限制。可以从源点向左边的每个点连接一条容量为2的边。

　　对于连到一个点的两条边的颜色不可以相同的限制，对于每一个点$u$新建$k$个点$u_1,u_2,...u_k$，并向它们连一条容量为1的边。这限制了每个点的每个颜色的出边至多只能有一条！

　　对于右边的点，我们镜像过去就好。

　　题目所连的边，我们按指定点的对应颜色，从左向右连接一条容量为1的边。

　　愉快地跑一次Dinic最大流。

　　由于题目保证一定有解，那么对于每一个连通块，块内所有点对应的2边一定是满流的。

　　也意味着，中间带颜色的边（即输入边），满流的就是答案经过的。

构造

　　现在我们只看答案经过的边，对于每个连通块直接模拟一笔画就好啦（随缘乱画），输出答案即可。

---

　　我的编号规则：

　　　　左边$n$个点：$[1,n]$

　　　　右边$n$个点：$(n,2n]$

　　　　每个点对应的$k$个颜色点：$(2n,2n+2nk]$。

　　　　源点：$2n+2nk+1$　　汇点：$2n+2nk+2$

　　（PS：这题的代码本来可以1A的然而输出的时候全部输出成最后一天了...天数和长度都对..看起来并没有什么不对...）

 #include <cstdio>
 #include <queue>
 #include <cstring>
 #include <vector>
 using namespace std;
 const int N=,INF=;
 int n,m,k,tot,h[],S,T,ch[N*][],chcnt,rec[][];
 int vis[],dis[],has[N*];
 vector<int> lis[N*],ans[N*];
 struct Edge{int v,f,next;}g[];
 queue<int> q;
 inline int addEdge(int u,int v,int f){
     g[++tot].v=v; g[tot].f=f; g[tot].next=h[u]; h[u]=tot;
     g[++tot].v=u; g[tot].f=; g[tot].next=h[v]; h[v]=tot;
     return tot-;
 }
 bool bfs(){
     memset(dis,-,sizeof dis);
     while(!q.empty()) q.pop();
     dis[S]=; q.push(S);
     int u,v;
     while(!q.empty()){
         u=q.front(); q.pop();
         for(int i=h[u];i;i=g[i].next)
             if(g[i].f&&dis[(v=g[i].v)]==-){
                 dis[v]=dis[u]+;
                 q.push(v);
             }
     }
     return dis[T]!=-;
 }
 int dinic(int u,int delta){
     if(u==T) return delta;
     int v,get,ret=;
     for(int i=h[u];i&&delta;i=g[i].next)
         if(g[i].f&&dis[(v=g[i].v)]==dis[u]+){
             get=dinic(v,min(g[i].f,delta));
             g[i].f-=get;
             g[i^].f+=get;
             delta-=get;
             ret+=get;
         }
     if(!delta) dis[u]=-;
     return ret;
 }
 int main(){
     scanf("%d%d%d",&n,&m,&k);
     tot=;
     S=n*+n**k+; T=S+;
     chcnt=n*;
     for(int i=;i<=n*;i++){
         if(i<=n) has[i]=addEdge(S,i,);
         else has[i]=addEdge(i,T,);
         for(int j=;j<=k;j++){
             ch[i][j]=++chcnt;
             if(i<=n) addEdge(i,ch[i][j],);
             else addEdge(ch[i][j],i,);
         }
     }
     for(int i=,x,y,z;i<=m;i++){
         scanf("%d%d%d",&x,&y,&z);
         rec[i][]=addEdge(ch[x][z],ch[y+n][z],);
         rec[i][]=x; rec[i][]=y+n;
     }
     while(bfs())
         dinic(S,INF);
     for(int i=;i<=m;i++){
         int u=rec[i][],v=rec[i][],id=rec[i][];
         if(!g[id].f&&!g[has[u]].f&&!g[has[v]].f){
             lis[u].push_back(v);
             lis[v].push_back(u);
         }
     }
     int day=;
     for(int i=;i<=n;i++)
         if(!vis[i]){
             vis[i]=;
             ans[++day].push_back(i);
             for(int u=i,go=-;go!=i;u=go){
                 if(!vis[lis[u][]]) go=lis[u][];
                 else if(!vis[lis[u][]]) go=lis[u][];
                 else break;
                 vis[go]=;
                 ans[day].push_back(go);
             }
             ans[day].push_back(i);
         }
     printf("%d\n",day);
     for(int i=;i<=day;i++){
         int siz=ans[i].size();
         printf("%d ",siz);
         for(int j=;j<siz;j++)
             if(ans[i][j]<=n) printf("L%d ",ans[i][j]);
             else printf("R%d ",ans[i][j]-n);
         puts("");
     }
     return ;
 }

奇妙代码