noip 2011

铺地毯

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入输出格式

输入格式：

输入文件名为carpet.in 。

输入共n+2 行。

第一行，一个整数n ，表示总共有 n 张地毯。

接下来的n 行中，第 i+1 行表示编号i 的地毯的信息，包含四个正整数 a ，b ，g ，k ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a ，b ）以及地毯在x轴和y 轴方向的长度。

第n+2 行包含两个正整数 x 和y，表示所求的地面的点的坐标（x ，y）。

输出格式：

输出文件名为carpet.out 。

输出共1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1 。

输入输出样例

输入样例#1：

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

输出样例#1：

3

输入样例#2：

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

输出样例#2：

-1

说明

【样例解释1】

如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2,2）的最上面一张地毯是 3 号地毯。

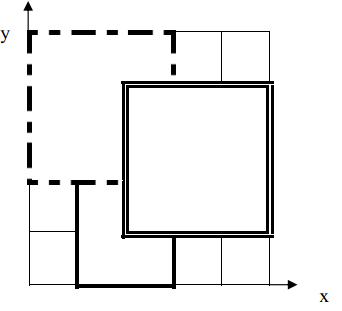
【数据范围】

对于30% 的数据，有 n ≤2 ；

对于50% 的数据，0 ≤a, b, g, k≤100；

对于100%的数据，有 0 ≤n ≤10,000 ，0≤a, b, g, k ≤100,000。

noip2011提高组day1第1题

思路：

这道题挺水的。。

so最开始：

看来并不是那么裸，我们来想一个办法让他不MLE。

先看一下30分代码。。。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
int n,a,b,x,y,ans[N][N];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int main()
{
    n=read();
    ;i<=n;i++)
    {
        a=read(),b=read(),x=read(),y=read();
        for(int i=a;i<a+x;i++)
         for(int j=b;j<b+y;j++)
          ans[i][j]++;
    }
    x=read(),y=read();
    ) {printf(;}
    printf("%d",ans[x][y]);
    ;
}

正解：(*^__^*) ……

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
int n,a[N],b[N],x[N],y[N],xx,yy,ans;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int main()
{
    n=read();
    ;i<=n;i++)
      a[i]=read(),b[i]=read(),x[i]=read(),y[i]=read();
    xx=read(),yy=read();
    ;i<=n;i++)
     {
         if(a[i]+x[i]>=xx&&a[i]<=xx&&b[i]+y[i]>=yy&&b[i]<=yy)
          ans=i;
     }
    ) {printf(;}
    printf("%d",ans);
    ;
}

计算系数

题目描述

给定一个多项式(by+ax)^k，请求出多项式展开后x^n*y^m 项的系数。

输入输出格式

输入格式：

输入文件名为factor.in。

共一行，包含5 个整数，分别为 a ，b ，k ，n ，m，每两个整数之间用一个空格隔开。

输出格式：

输出共1 行，包含一个整数，表示所求的系数，这个系数可能很大，输出对10007 取模后的结果。

输入输出样例

输入样例#1：

1 1 3 1 2

输出样例#1：

3

说明

【数据范围】

对于30% 的数据，有 0 ≤k ≤10 ；

对于50% 的数据，有 a = 1，b = 1；

对于100%的数据，有 0 ≤k ≤1,000，0≤n, m ≤k ，且n + m = k ，0 ≤a ，b ≤1,000,000。

noip2011提高组day2第1题

思路：

我们先弄懂样例，然后从简单的数据找规律。

通过下式我们可以发现

（a*x+b*y）^2=(a*x)^2+2*a*b*x*y+(b*y)^2

（a*x+b*y）^3=(a*x)^3+3*(a^2)*b*(x^2)*y+3*a*(b^2)*x*(y^2)+(b*y)^3

（a*x+b*y）^4=(a*x)^4+4*(a^3)*b*(x^3)*y+6*(a^2)*(b^2)*(x^2)*(y^2)+4*a*(b^3)*x*(y^3)+(b*y)^3 

（a*x+b*y）^5=......

式x^n*y^m的系数为t*a^n*b^m,而t值正好是

1 2 1 

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

有经验的同学可以一眼看出这就是杨辉三角。

那有的同学没有接触过就会问了杨辉三角是什么？？

没关系，来我们来看一下杨辉三角

简单的说，就是两个未知数和的幂次方运算后的系数问题，比如（x+y）²=x²+2xy+y²，这样系数就是1,2,1这就是杨辉三角的其中一行，立方，四次方，运算的结果看看各项的系数，你就明白其中的道理了。——摘自搜狗百科

基本应用

与杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。

例如，在杨辉三角中，第3行的第三个数恰好对应着两数和的平方的展开式的每一项的系数，

即(a+b)^2;=a^2+2ab+b^2

第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数

即(a+b)^3=a^3+3a^2b+3ab^2+b^3

以此类推。

又因为性质6：第n行的m个数可表示为C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

因此可得出二项式定理的公式为：(a+b)^n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+C(n,n)a^0*b^n

规律：

前提：端点的数为1.

1、每个数等于它上方两数之和。

2、每行数字左右对称，由1开始逐渐变大。

3、第n行的数字有n项。

4、第n行数字和为2^(n-1)。

5、第n行的第m个数和第n-m+1个数相等，即C(n-1,m-1)=C(n-1,n-m)，这是组合数性质

性质6的公式表述之一

6、每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。

7、第n行的m个数可表示为C(n-1,m-1)（n-1下标，m-1上标），即为从n-1个不同

杨辉三角的组合数表示元素中取m-1个元素的组合数。

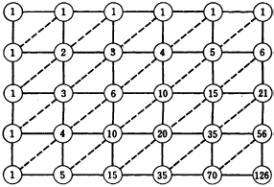帕斯卡三角形组合数计算方法：C(n,m)=n!/[m!(n-m)!]

8、(a+b)^n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。

9、将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。

10、将各行数字相排列，可得11的N次方：1=11º 11=11¹ 121=11²

f[i,j]:=f[i-1,j-1]+f[i-1,j];

结果：ans=f[k,k-n+1]*(a^n)*(b^m)

由于题目要求输出对10007 取模后的结果，则有：

f[i,j]:=（(f[i-1,j-1] mod 10007)+(f[i-1,j]mod 10007))mod 10007;

a^n=((a^(N-1))mod 10007*a)mod 10007

b^m=((b^(m-1))mod 10007*b)mod 10007

(a^n可以边乘边取余数的方法做，也可用快速幂）。

注意：边界条件k=0，k=n等。

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1001
#define mod 10007
using namespace std;
int a,b,k,n,m;
int f[N][N];
;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-';  ch=getchar();}
    return x*f;
}
int main()
{
    a=read(),b=read(),k=read(),n=read(),m=read();
    ;i<=k;i++)
     {
         f[i][]=;f[i][i]=;
         ;j<i;j++)
         f[i][j]=(f[i-][j]+f[i-][j-])%mod;
     }
    ;i<=n;i++) ans=(ans*a)%mod;//(a^n)
    ;i<=m;i++) ans=(ans*b)%mod;//b^m
    ans=(ans*f[k][m])%mod;
    cout<<ans;
    ;
}

选择客栈

题目描述

丽江河边有n 家很有特色的客栈，客栈按照其位置顺序从 1 到n 编号。每家客栈都按照某一种色调进行装饰（总共 k 种，用整数 0 ~ k-1 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 p 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 p元的咖啡店小聚。

输入输出格式

输入格式：

输入文件hotel.in，共n+1 行。

第一行三个整数n ，k ，p，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的n 行，第 i+1 行两个整数，之间用一个空格隔开，分别表示 i 号客栈的装饰色调和i 号客栈的咖啡店的最低消费。

输出格式：

输出文件名为hotel.out 。

输出只有一行，一个整数，表示可选的住宿方案的总数。

输入输出样例

输入样例#1：

5 2 3
0 5
1 3
0 2
1 4
1 5

输出样例#1：

3

说明

【输入输出样例说明】

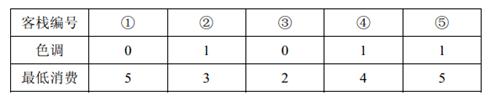
2 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈①③，②④，②⑤，④⑤，但是若选择住4 、5 号客栈的话，4 、5 号客栈之间的咖啡店的最低消费是4 ，而两人能承受的最低消费是3 元，所以不满足要求。因此只有前 3 种方案可选。

【数据范围】

对于30% 的数据，有 n ≤100；

对于50% 的数据，有 n ≤1,000；

对于100%的数据，有 2 ≤n ≤200,000，0<k ≤50，0≤p ≤100 ， 0 ≤最低消费≤100。

思路：

这个题有些·。。。

我看了半天题解没看懂，最后不知道怎么着突然开窍了。。。

这道题我使用递归做的。

对于一个状态他可以有两个来向，一是他本身的价格低于最大承受价格，这样的话无论从哪个和它相同颜色的旅店都可以和他配对，也就是说到他这我们所拥有的方案数为它上一个状态+与这个旅店的颜色相同的酒店数，也就是f[i]=f[i-1]+sum[pue[i]].（为何是这样？？ 我们想啊，如果这个点的价值及已经小于最低承受价值了，那么所有到这个点的旅店都满足要求）

还有一种情况是他自身价格大于最低承受价值那么我们就要考虑从其他地方到这个点的旅店中有没有小于最低承受价值的，若没有s++（并且他这个点的他们的颜色相同），那这个状态的方案数即为：f[i]=f[i-1]+sum[pue[i]]-s（只有s个旅店不满足要求）.

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 200010
using namespace std;
int n,m,p,x,s,ans;
];
bool cost[N];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-';  ch=getchar();}
    return x*f;
}
int main()
{
    n=read(),m=read(),p=read();
    ;i<=n;i++)
    {
        hue[i]=read(),x=read();
        ;
    }
    ++sum[hue[]];
    ;i<=n;i++)
    {
        if(!cost[i])
          f[i]=f[i-]+sum[hue[i]];
        else
        {
            s=;
            ;j>=;j--)
            {
                if(!cost[j]) break;
                if(hue[i]==hue[j]) s++;
            }
            f[i]=f[i-]+sum[hue[i]]-s;
        }
        ++sum[hue[i]];
     }
    printf("%d",f[n]);
    ;
}

观光公交

题目描述

风景迷人的小城Y 市，拥有n 个美丽的景点。由于慕名而来的游客越来越多，Y 市特意安排了一辆观光公交车，为游客提供更便捷的交通服务。观光公交车在第 0 分钟出现在 1号景点，随后依次前往 2、3 、4 ……n 号景点。从第 i 号景点开到第 i+1 号景点需要 Di 分钟。任意时刻，公交车只能往前开，或在景点处等待。

设共有m 个游客，每位游客需要乘车1 次从一个景点到达另一个景点，第i 位游客在Ti 分钟来到景点 Ai ，希望乘车前往景点Bi （Ai<Bi ）。为了使所有乘客都能顺利到达目的地，公交车在每站都必须等待需要从该景点出发的所有乘客都上车后才能出发开往下一景点。

假设乘客上下车不需要时间。

一个乘客的旅行时间，等于他到达目的地的时刻减去他来到出发地的时刻。因为只有一辆观光车，有时候还要停下来等其他乘客，乘客们纷纷抱怨旅行时间太长了。于是聪明的司机ZZ给公交车安装了 k 个氮气加速器，每使用一个加速器，可以使其中一个 Di 减1 。对于同一个Di 可以重复使用加速器，但是必须保证使用后Di 大于等于0 。

那么ZZ该如何安排使用加速器，才能使所有乘客的旅行时间总和最小？

输入输出格式

输入格式：

输入文件名为bus.in。

第1 行是3 个整数n, m, k ，每两个整数之间用一个空格隔开。分别表示景点数、乘客数和氮气加速器个数。

第2 行是n-1 个整数，每两个整数之间用一个空格隔开，第i 个数表示从第i 个景点开往第i+1 个景点所需要的时间，即 Di 。

第3 行至m+2 行每行3 个整数 Ti, Ai, Bi，每两个整数之间用一个空格隔开。第 i+2 行表示第i 位乘客来到出发景点的时刻，出发的景点编号和到达的景点编号。

输出格式：

输出文件名为bus.out。共一行，包含一个整数，表示最小的总旅行时间。

输入输出样例

输入样例#1：

3 3 2
1 4
0 1 3
1 1 2
5 2 3

输出样例#1：

10

说明

【输入输出样例说明】

对D2 使用2 个加速器，从2 号景点到 3 号景点时间变为 2 分钟。

公交车在第1 分钟从1 号景点出发，第2 分钟到达2 号景点，第5 分钟从2 号景点出发，第7 分钟到达 3 号景点。

第1 个旅客旅行时间 7-0 = 7 分钟。

第2 个旅客旅行时间 2-1 = 1 分钟。

第3 个旅客旅行时间 7-5 = 2 分钟。

总时间 7+1+2 = 10分钟。

【数据范围】

对于10% 的数据，k=0 ；

对于20% 的数据，k=1 ；

对于40% 的数据，2 ≤ n ≤ 50，1 ≤ m ≤ 1,000，0 ≤ k ≤ 20，0 ≤ Di ≤ 10，0 ≤ T i ≤ 500；

对于60% 的数据，1 ≤ n ≤ 100，1 ≤ m ≤ 1,000，0 ≤ k ≤ 100 ，0 ≤ Di ≤ 100，0 ≤ T i ≤ 10,000 ；

对于100%的数据，1 ≤ n ≤ 1,000，1 ≤ m ≤ 10,000 ，0 ≤ k ≤ 100,000，0 ≤ Di ≤ 100 ，0 ≤ T i ≤ 100,000。

noip2011提高组day2第3题

思路：

这道题我用的模拟做的。详细思路在代码中

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
int n,m,k,ans;
int t[N],ti[N],js[N],end[N],tmax[N],timm[N],begin[N],people[N];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-';  ch=getchar();}
    return x*f;
}
int main()
{
    n=read(),m=read(),k=read();
    ;i<n;i++) ti[i]=read();
    ;i<=m;i++)
    {
        t[i]=read(),begin[i]=read(),end[i]=read();
        tmax[begin[i]]=max(tmax[begin[i]],t[i]);//由于列车只能往前走不能往后走，因此我们要等到没一个从该点上车的人都上车才能发车，这也就是最早发车时间
        people[end[i]]++;//最初存的是到达每一个终点的人
     }
    ;i<=n;i++) people[i]+=people[i-];//前面所有的人的个数，这样可以求出每一个站点上人的个数peo[i]-people[i-1]
    timm[]=;
    ;i<=n;i++) timm[i]=max(timm[i-],tmax[i-])+ti[i-];//到达第i个车站花费的最少的时间
    ;i<=m;i++) ans+=timm[end[i]]-t[i];//每一个乘客所需要的时间，他到达他的目的地所用的时间-他上车的时间 ，不用加速器的情况
    //到这个地方是不用加速器的情况，可以的10分(*^__^*) ……
    while(k--)//开始使用加速器
    {
        js[n]=n;js[n-]=n;
        ;i>=;i--)
        {
            ]<=tmax[i+]) js[i]=i+;
            ];
        }
        ,wz;
        ;i<=n;i++)
         )//看看在那个地方使用加速器可以使更多的人减小旅行时间，前提他必须时间为正数
          maxn=people[js[i]]-people[i],wz=i;//统计最多能使几个人减小旅行时间，wz为在那个地方放加速器
        ti[wz]--; ans-=maxn;timm[]=;//放加速器后使每一个地点的时间减少一
        ;i<=n;i++)
         timm[i]=max(timm[i-],tmax[i-])+ti[i-];//减速之后进行重置
    }
    printf("%d",ans);
    ;
}

聪明的质监员

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 n 个矿石，从 1到n 逐一编号，每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是：

1 、给定m 个区间[Li,Ri]；

2 、选出一个参数 W；

3 、对于一个区间[Li,Ri]，计算矿石在这个区间上的检验值Yi：

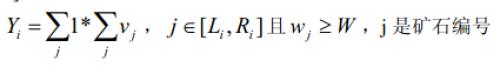
这批矿产的检验结果Y 为各个区间的检验值之和。即：Y1+Y2...+Ym

若这批矿产的检验结果与所给标准值S 相差太多，就需要再去检验另一批矿产。小T

不想费时间去检验另一批矿产，所以他想通过调整参数W 的值，让检验结果尽可能的靠近

标准值S，即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

输入文件qc.in 。

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n 行，每行2个整数，中间用空格隔开，第i+1 行表示 i 号矿石的重量 wi 和价值vi。

接下来的m 行，表示区间，每行2 个整数，中间用空格隔开，第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意：不同区间可能重合或相互重叠。

输出格式：

输出文件名为qc.out。

输出只有一行，包含一个整数，表示所求的最小值。

输入输出样例

输入样例#1：

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3 

输出样例#1：

10

说明

【输入输出样例说明】

当W 选4 的时候，三个区间上检验值分别为 20、5 、0 ，这批矿产的检验结果为 25，此

时与标准值S 相差最小为10。

【数据范围】

对于10% 的数据，有 1 ≤n ，m≤10；

对于30% 的数据，有 1 ≤n ，m≤500 ；

对于50% 的数据，有 1 ≤n ，m≤5,000；

对于70% 的数据，有 1 ≤n ，m≤10,000 ；

对于100%的数据，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

思路：

这道题可以说是比较裸的一个二分题了吧。

在处理时我们要处理出

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 200010
#define LL long long
using namespace std;
LL  n,m,s,L,R=1LL<<50,ans=1LL<<50,mid;
LL  w[N],v[N],l[N],r[N],sumv[N],sumamount[N];
LL  read()
{
	LL x=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';  ch=getchar();}
	return x*f;
}
bool check(LL x)
{
	LL ret=s; bool flag=false;
	for(int i=1;i<=n;i++)
	{
		sumamount[i]=sumamount[i-1];
		sumv[i]=sumv[i-1];
		if(w[i]<x) continue;
		sumamount[i]++; sumv[i]+=v[i];
	 }
	for(int i=1;i<=m;i++)
	 ret-=(sumamount[r[i]]-sumamount[l[i]-1])*(sumv[r[i]]-sumv[l[i]-1]);
	if(ret<0) ret=-ret,flag=true;
	ans=min(ans,ret);
	return flag;
}
int main()
{
    n=read(),m=read(),s=read();
    for(LL i=1;i<=n;i++)
     w[i]=read(),v[i]=read();
    for(LL i=1;i<=m;i++)
     l[i]=read(),r[i]=read();
    while(L<=R)
    {
    	mid=L+R>>1;
    	if(check(mid)) L=mid+1;
    	else R=mid-1;
	}
	printf("%lld",ans);
	return 0;
}