手写AVL平衡二叉搜索树

手写AVL平衡二叉搜索树

二叉搜索树的局限性

先说一下什么是二叉搜索树，二叉树每个节点只有两个节点，二叉搜索树的每个左子节点的值小于其父节点的值，每个右子节点的值大于其左子节点的值。如下图：

二叉搜索树，顾名思义，它的搜索效率很高，可以达到O(logn)。但这是理想状况下的，即上图所示。实际上，由于插入顺序的原因，形成的二叉搜索树并不会像上图这样“工整”，最坏的情况的下，甚至可能会退化成链表了，如下图：

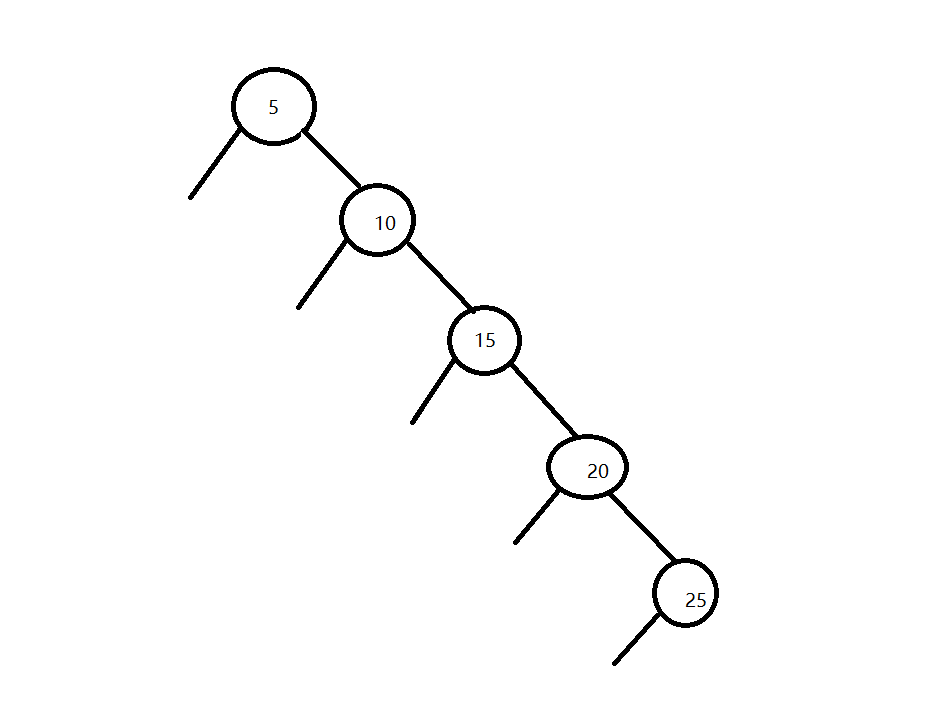
这显然不是我们想要看的结果，那么我们必须要引入一套机制来避免这种事情的发生，也就是让二叉搜索树带上平衡条件。

AVL平衡二叉搜索树

几个基本概念

• 叶子节点：既没有左子节点，也没有右左子节点的节点就是叶子节点。

• 树的高度：叶子节点的高度为1，空节点的高度是-1，父节点的高度是其两个子树较高一棵子树的高度加一。

• 平衡条件：每一个节点的左子树与右子树的高度差不超过1。

核心思想

因为AVL平衡二叉搜索树，父节点的两颗子树的高度差不能超过1。在AVL平衡二叉树种，采用旋转的机制来使不满足平衡条件的二叉树重新回到满足平衡条件的状态。在二叉搜索树中，需要被平衡的情况可以分为两大类总共四种情况，

• 单旋转
  • 左旋转
  • 右旋转
• 双旋转
  • 先左旋，再右旋
  • 先右旋，再左旋

如下图所示：

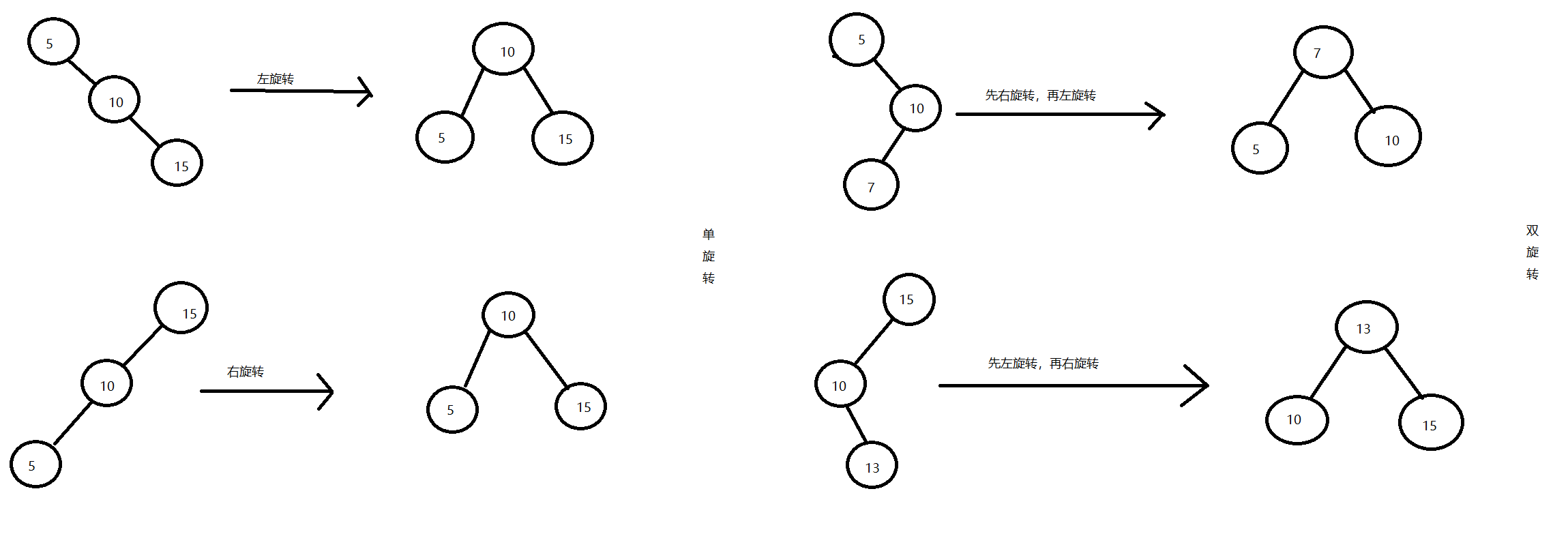
通过图片的形式我们很容易就可以写出使二叉树回到满足平衡条件的代码

// 右旋转
public TreeNode rightRotate(TreeNode root) {
        TreeNode temp1 = root.left;
        TreeNode temp2 = temp1.right;
        temp1.right = root;
        root.left = temp2;
        return temp1;
}

// 左旋转
public TreeNode leftRotate(TreeNode root) {
    TreeNode temp1 = root.right;
    TreeNode temp2 = temp1.left;
    temp1.left = root;
    root.right = temp2;
    return temp1;
} 

// 先右后左
public TreeNode rightLeftRotate(TreeNode root) {
    root.right = rightRotate(root.right);
    return leftRotate(root);
}

// 先左后右
public TreeNode leftRightRotate(TreeNode root) {
    root.left = leftRotate(root.left);
    return rightRotate(root);
}

我们必须再每一次插入节点后判断树是否需要平衡，也就是是否会出现两颗子树的高度差超过1的情况，首先编写一个可以计算出传入节点 高度的函数。

public int height(TreeNode root) {
    if (root == null) {
        return -1;
    }
    if (root.left == null && root.right == null) {
        return 0;
    }
    return Math.max(height(root.right), height(root.left));
}

有了这个函数，我们就不仅可以判断是否出现需要平衡的情况，还可以判断需要平衡的情况是四种情况种的哪一种。

public TreeNode balance(TreeNode root) {
    int l = height(root.left);
    int r = height(root.right);
    if (l - r >= 2) {
        // rightRotate
        if (height(root.left.left) - height(root.left.right) >= 1) {
            // rightRotate
            root = rightRotate(root);
        } else if (height(root.left.right) - height(root.left.left) >= 1) {
            // leftRightRotate
            root = leftRightRotate(root);
        }
    } else if (r - l >= 2) {
        // leftRotate
        if (height(root.right.right) - height(root.right.left) >= 1) {
            // leftRotate
            root = leftRotate(root);
        } else if (height(root.right.left) - height(root.right.right) >= 1){
            root = rightLeftRotate(root);
        }
    }
    return root;
}

以上就是AVL平衡二叉搜索树的精髓，并且已经用代码实现了。

完整代码

这是我完善后的功能相对完整的AVL二叉搜索平衡树。

class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    int height;

    public TreeNode(int value) {
        this.value = value;
    }
}

public class AVLBinarySearchTree {

    public static void main(String[] args) {
        AVLBinarySearchTree a = new AVLBinarySearchTree();
        for (int i = 0; i < 10; i++) {
            a.insert(i);
        }
    }

    private TreeNode root;
    private static final int ALLOWED_IMBALANCE = 1;

    // 删除元素
    public void remove(int value) {
        root = remove(value, root);
    }

    // 检查是否包含某一元素，包含则返回该节点，不包含则返回null
    public TreeNode contain(int value) {
        TreeNode temp = root;
        if (temp == null) {
            return temp;
        }
        while (temp.value != value) {
            if (value > temp.value) {
                temp = temp.right;
            } else if (value < temp.value) {
                temp = temp.left;
            }
        }
        return temp;
    }

    // 删除指定子树上的指定元素
    private TreeNode remove(int value, TreeNode abn) {
        if (abn == null) {
            return abn;
        }

        if (value > abn.value) {
            abn.right = remove(value, abn.right);
        } else if (value < abn.value) {
            abn.left = remove(value, abn.left);
        } else {
            if (abn.right == null && abn.left == null) {
                abn = null;
                return abn;
            } else if (abn.right != null) {
                abn.value = findMin(abn.right).value;
                abn.right = remove(abn.value, abn.right);
            } else {
                abn.value = findMax(abn.left).value;
                abn.left = remove(abn.value, abn.left);
            }

        }

        return balance(abn);
    }

    // 找到指定子树最大值
    private TreeNode findMax(TreeNode abn) {
        if (abn == null) {
            return null;
        }
        TreeNode temp = abn;
        while (temp.right != null) {
            temp = temp.right;
        }
        return temp;

    }

    // 找到指定子树最小值
    private TreeNode findMin(TreeNode abn) {
        if (abn == null) {
            return null;
        }
        TreeNode temp = abn;
        while (temp.left != null) {
            temp = temp.left;
        }
        return temp;
    }

    // 插入节点
    public void insert(int value) {
        root = insert(value, root);
    }

    // 计算节点高度
    private int height(TreeNode abn) {
        if (abn == null) {
            return -1;
        }
        return abn.height;
    }

    // 树的高度
    public int height() {
        return height(root);
    }

    // 插入节点
    private TreeNode insert(int value, TreeNode abn) {
        if (abn == null) {
            return new TreeNode(value);
        }
        if (value > abn.value) {
            abn.right = insert(value, abn.right);
        } else if (value < abn.value) {
            abn.left = insert(value, abn.left);
        }
        return balance(abn);
    }

    // 平衡不平衡的树
    private TreeNode balance(TreeNode abn) {
        if (height(abn.left) - height(abn.right) > ALLOWED_IMBALANCE) {
            if (height(abn.left.left) >= height(abn.left.right)) {
                abn = leftSingleRotate(abn);
            } else if (height(abn.left.left) < height(abn.left.right)) {
                abn = leftDoubleRotate(abn);
            }
        } else if (height(abn.right) - height(abn.left) > ALLOWED_IMBALANCE) {
            if (height(abn.right.right) >= height(abn.right.left)) {
                abn = rightSingleRotate(abn);
            } else {
                abn = rightDoubleRotate(abn);
            }
        }
        abn.height = Math.max(height(abn.left), height(abn.right)) + 1;
        return abn;
    }

    // 右单旋转
    private TreeNode rightSingleRotate(TreeNode abn) {
        TreeNode temp = abn;
        abn = abn.right;
        temp.right = abn.left;
        abn.left = temp;
        temp.height = Math.max(height(temp.right), height(temp.left)) + 1;
        abn.height = Math.max(height(abn.right), temp.height) + 1;
        return abn;
    }

    // 左单旋转
    private TreeNode leftSingleRotate(TreeNode abn) {
        TreeNode temp = abn;
        abn = abn.left;
        temp.left = abn.right;
        abn.right = temp;
        temp.height = Math.max(height(temp.right), height(temp.left)) + 1;
        abn.height = Math.max(height(abn.right), temp.height) + 1;
        return abn;
    }

    // 右双旋转
    private TreeNode rightDoubleRotate(TreeNode abn) {
        abn.right = leftSingleRotate(abn.right);
        return rightSingleRotate(abn);
    }

    // 左双旋转
    private TreeNode leftDoubleRotate(TreeNode abn) {
        abn.left = rightSingleRotate(abn.left);
        return leftSingleRotate(abn);
    }
}