[luogu]P4364 [九省联考2018]IIIDX

题目背景

Osu 听过没？那是Konano 最喜欢的一款音乐游戏，而他的梦想就是有一天自己也能做个独特酷炫的音乐游戏。现在，他在世界知名游戏公司KONMAI 内工作，离他的梦想也越来越近了。

这款音乐游戏内一般都包含了许多歌曲，歌曲越多，玩家越不易玩腻。同时，为了使玩家在游戏上氪更多的金钱花更多的时间，游戏一开始一般都不会将所有曲目公开，有些曲目你需要通关某首特定歌曲才会解锁，而且越晚解锁的曲目难度越高。

题目描述

$这一天，Konano 接到了一个任务，他需要给正在制作中的游戏《IIIDX》安排曲目的解锁顺序。游戏内共有n 首曲目，每首曲目都会有一个难度d，游戏内第i 首曲目会在玩家Pass 第\lfloor \frac{i}{k} 首曲目后解锁（\lfloor x 为下取整符号）若\lfloor \frac{i}{k} = 0，则说明这首曲目无需解锁$

$举个例子：当k = 2 时，第1 首曲目是无需解锁的（\lfloor \frac{1}{2} \rfloor = 0），第7 首曲目需要玩家Pass 第\lfloor \frac{7}{2} \rfloor = 3 首曲目才会被解锁。$

$Konano 的工作，便是安排这些曲目的顺序，使得每次解锁出的曲子的难度不低于作为条件需要玩家通关的曲子的难度，即使得确定顺序后的曲目的难度对于每个i 满足$

$d_i \geq d_{\lfloor \frac{i}{k} \rfloor}$

$当然这难不倒曾经在信息学竞赛摸鱼许久的Konano。那假如是你，你会怎么解决这份任务呢?$

输入输出格式

输入格式：

从文件iiidx.in 中读入数据。

第1 行1 个正整数n 和1 个小数k，n 表示曲目数量，k 其含义如题所示。

第2 行n 个用空格隔开的正整数d，表示这n 首曲目的难度。

输出格式：

输出到文件iiidx.out 中。

输出1 行n 个整数，按顺序输出安排完曲目顺序后第i 首曲目的难度。

若有多解，则输出d1 最大的；若仍有多解，则输出d2最大的，以此类推。

输入输出样例

输入样例#1： 复制

4 2.0

114 514 1919 810

输出样例#1： 复制

114 810 514 1919

说明

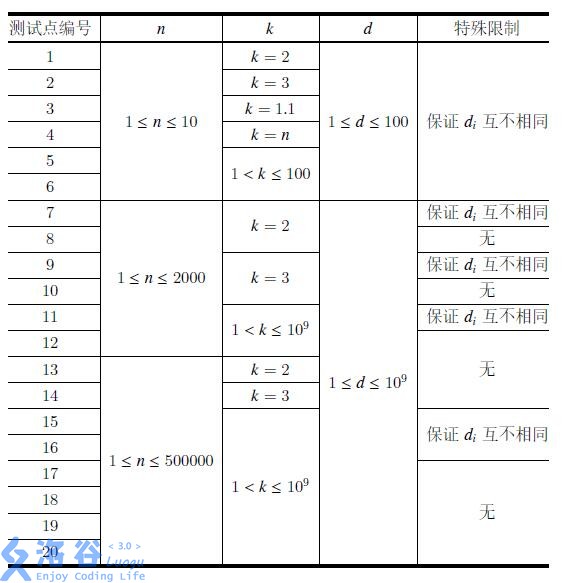
题解

如果第三题暴力不能水过去的话，这道题应该算还好吧。

但是现在看来这道题才是day1最难的一题吧。（巨佬请无视

所以这道题大概我是只能口胡的。

对于55分很显然我们直接dfs到叶子节点然后从大到小一一赋值。

对于满分我们要处理值相同的情况。

就需要我们预处理一个$f[]$数组来满足当前位置前面还有多少可以选。

通过线段树维护$f[]$数组来保证预留位置使前面的子节点可以选。

最主要的是我们要对于一个相同的值，减去相同值末尾的以后的$f[]$，而不是从这个值开始往后减，这样就能避免重复带来的影响了。

至于道理我是不懂的。我只知道实现，反正在我看来这是一道贪心神仙题。

Code

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e6+5;
int sum[N<<2],lazy[N<<2];
int a[N],n,ans[N],size[N],fa[N],nxt[N];
double k;
int read(){
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}
void build(int root,int left,int right){
    int mid=(left+right)>>1;
    if(left==right){
        sum[root]=left;return ;
    }build(root<<1,left,mid);build(root<<1|1,mid+1,right);
    sum[root]=min(sum[root<<1],sum[root<<1|1]);
}
void push(int root,int left,int right){
    sum[root<<1]+=lazy[root];sum[root<<1|1]+=lazy[root];
    lazy[root<<1]+=lazy[root];lazy[root<<1|1]+=lazy[root];
    lazy[root]=0;
}
void update(int root,int left,int right,int l,int r,int v){
    if(left>r||right<l)return ;
    if(lazy[root])push(root,left,right);
    if(left>=l&&right<=r){
        sum[root]+=v;lazy[root]+=v;
        return ;
    }int mid=(left+right)>>1;
    if(mid>=l) update(root<<1,left,mid,l,r,v);
    if(mid<r)  update(root<<1|1,mid+1,right,l,r,v);
    sum[root]=min(sum[root<<1],sum[root<<1|1]);
}
int query(int root,int left,int right,int k){
    if(left==right){
        return sum[root]>=k?left:left+1;
    }int mid=(left+right)>>1;
    if(lazy[root])push(root,left,right);
    if(sum[root<<1|1]>=k) return query(root<<1,left,mid,k);
    else return query(root<<1|1,mid+1,right,k);
}
bool cmp(int a,int b){return a>b;}
int main(){
    n=read();cin>>k;
    for(int i=1;i<=n;i++)a[i]=read();sort(a+1,a+n+1,cmp);
    for(int i=n;i>=1;i--){
        nxt[i]=i;fa[i]=(1.0*i/k);
        size[i]++;size[fa[i]]+=size[i];
        if(a[i]==a[i+1])nxt[i]=nxt[i+1];
    }build(1,1,n);
    for(int i=1;i<=n;i++){
        if(fa[i]&&fa[i]!=fa[i-1])update(1,1,n,ans[fa[i]],n,size[fa[i]]-1);
        int tmp=nxt[query(1,1,n,size[i])];ans[i]=tmp;
        update(1,1,n,tmp,n,-size[i]);
    }
    for(int i=1;i<=n;i++)cout<<a[ans[i]]<<' ';
    return 0;
}