【图论】最短路问题之spfa

写在算法前面：

前向星存图（一个神奇的超越邻接矩阵的存在）

首先讲一下需要定义的一些东西？？

1.head数组：head[点数]：head[i]表示以当前点i为起点的最后一条边（这里的最后指的是编号【我们按输入顺序给边编一个号】）。

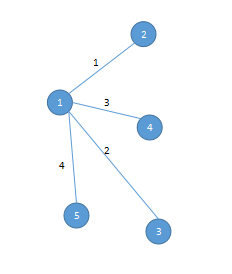
这个图即为head[1]=4，表示以1为起点的边的最后一条是点1—>点5编号为4的边；

2.num_edge，表示边的总个数；

3.结构体：

struct Edge{
    int next,to,dis;
}edge[边数];

这里，edge[i].next表示上一条以i为起点的边：：

还是上面那个图，这里edge[4].next=3；

edge[i].to表示这条边i的终点；

edge[i].dis表示这条边的权值；

存图

void addedge(int from,int to,int dis){
    num_edge++;//因为存入一条边，总边数+1;
    edge[num_edge].next=head[from];//新存入一条以from为起点的边，之前的以from为起点的最后一条边变成了新边的上一条边
    edge[num_edge].to=to;//存终点
    edge[num_edge].dis=dis;//存权值
    head[from]=num_edge;//存入一条以from为起点的边，那么现在以from为起点的最后一条边就是新存入的边
}

提醒：如果要存的是无向图，进行程序时应该：addedge(from,to,dis)，addedge(to,from,dis)各跑一遍，所开空间也要*2；

大概是讲完了链式前向星存图；

spfa

算法思想：

1.运用队列的思想，先把起点入队，更新起点能够到达的点，更新这些点到起点的伪最短路（因为可能还有更短情况）然后把得到更新的点中不在队列里的加入队列，以便更新其他点。

2.当前更新的是伪最短路即可能会有更优情况

eg：起点是1，1到6距离为7，加入队列dis[6]=7，而1到7距离为2，7到6距离为3，会将dis[6]更新为2+3=5。所以一遍一遍查，最后将会是最短路。

时间复杂度大约是O（ke），稀疏图中k约等于2，但是毒瘤数据会把复杂度卡成O（nm）；

spfa在存图基础上再开vis[点数]查询某个点是否已经在队列里，避免重复入队（请注意，是是否在队列里 队列里 队列里）

dis[点数]用来存某个点到起点的最短路；

以洛谷p3371【模板】单源最短路径（弱化版） 为例纸（标准的过不去qwq）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>

using namespace std;

const int inf=;//题目要求的初始值

queue <int> q;//定义一个队列q
int n,m,s;
int head[],num;
int vis[],dis[];

struct Edge{
    int next,to,dis;
}edge[];

void addedge(int from,int to,int dis){//加边
    num++;
    edge[num].next=head[from];
    edge[num].to=to;
    edge[num].dis=dis;
    head[from]=num;
}

void spfa(){
    for(int i=;i<=n;i++){//首先初始化，将所有点的dis赋值为2147483647，所有点都不在队列里，vis为0
        dis[i]=inf;
        vis[i]=;
    }
    q.push(s);//把起点入队
    dis[s]=;//起点到起点，最短路为0
    vis[s]=;//入队了，vis变为1
    while(!q.empty()){//开始循环
        int u=q.front();
        q.pop();//把队首元素出队
        vis[u]=;//出队了，vis重置为0（因为可能还有更近的下次还能循环到）
        for(int i=head[u];i;i=edge[i].next){//遍历以u为起点的所有遍
            int v=edge[i].to;//v为终点
            if(dis[v]>dis[u]+edge[i].dis){//如果之前的最短路比由u点出发再”拐弯“的点的要大，显然他不是最短，更新他
                dis[v]=dis[u]+edge[i].dis;
                if(!vis[v]){//如果终点不在队列里，入队
                    q.push(v);
                    vis[v]=;
                }
            }
        }
    }
}

int main(){
    scanf("%d%d%d",&n,&m,&s);
    int u,v,w;
    for(int i=;i<=m;i++){
        scanf("%d%d%d",&u,&v,&w);//输入起点终点权值
        addedge(u,v,w);//加边
    }
    spfa();//核心
    for(int i=;i<=n;++i)
    {
        if(i==s) printf("0 ");
        else printf("%d ",dis[i]);
    }
    return ;
}

end-