查找、AVL树、散列表

插值查找是二分查找的改进，斐波那契查找是插值查找的改进。

二分查找：mid=（low+high）/  2

插值查找：mid=（key-a[low]）*(high-low)/  （a[high]-a[low]）

斐波那契查找主要思想是只要长度符合斐波那契数列，则该段数字可以用两个子段来分割，F（k）-1=(F[k-1]-1)+(F[k-2]-1),即mid=low+F(k-1)-1

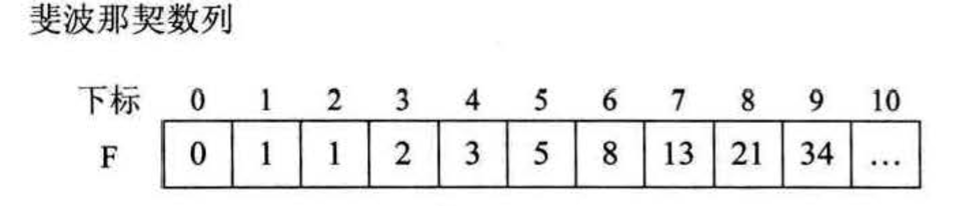
FibonacciSearch查找的实现:

package Fibonacci_Search;

//fibonacci数列查找
public class FibonacciSearch {

    //fibonacci数列
    public static int fib(int n)
    {
        if(n==0)
            return 0;
        if(n==1)
            return 1;
        return fib(n-1)+fib(n-2);
    }

    //查找
    public static int fibonacci_search(int[] arr,int n,int key)
    {
        int low=1;  //记录从1开始
        int high=n;     //high不用等于fib(k)-1，效果相同
        int mid;

        int k=0;
        while(n>fib(k)-1)    //获取k值
            k++;
        int[] temp = new int[fib(k)];   //因为无法直接对原数组arr[]增加长度，所以定义一个新的数组
        System.arraycopy(arr, 0, temp, 0, arr.length); //采用System.arraycopy()进行数组间的赋值
        for(int i=n+1;i<=fib(k)-1;i++)    //对数组中新增的位置进行赋值
            temp[i]=temp[n]; 

        while(low<=high) {
            mid=low+fib(k-1)-1;
            if(temp[mid]>key) {
                high=mid-1;
                k=k-1;  //对应上图中的左段，长度F[k-1]-1
            }else if(temp[mid]<key) {
                low=mid+1;
                k=k-2;  //对应上图中的右端，长度F[k-2]-1
            }else {
                if(mid<=n)
                    return mid;
                else
                    return n;       //当mid位于新增的数组中时，返回n
            }
        }
        return 0;
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] arr = {0,1,16,24,35,47,59,62,73,88,99};
        int n=10;
        int key=59;
        System.out.println(fibonacci_search(arr, n, key));  //输出结果为：6
    }

}

测试结果:6

---

---

排序二叉树，排序二叉树是一种动态查找表，方便插入和删除数据。利用中序遍历二叉排序树可以得到有序数列

排序二叉树的删除操作有4种可能。

1）没有左子树的结点，直接将右子树连接到前驱上。

2）没有右子树的结点，直接将左子树连接到前驱上。

3）叶子节点，直接删除

4）有左子树和右子树，可以选取左子树的中序遍历前驱结点或者后继结点替代该结点。

仔细观察，第四种情况中，前驱结点和后继结点肯定属于1，2，3两种情况中的一种，直接将要删除的结点替换成该结点的值并将该结点删除即可。

排序二叉树的实现：

package Binary_Sort_Tree;

//二叉排序树
public class BinarySortTree {

    /**
     * 根结点
     */
    private TreeNode rootNode;

    /**
     * 获取rootNode
     * @return
     */
    public TreeNode getRootNode() {
        return this.rootNode;
    }

    /**
     * 创建二叉排序树 的第一种方法（通过insertBST创建）
     * @param array
     * @return
     */
    public void createBinarySortTree1(int[] array) {

        for (int i = 0; i <array.length; i++) {
            if (!insertBST(array[i])) {
                System.out.println("已存在" + array[i] + "，不再插入二叉排序树");
            }
        }

    }

    /**
     * 创建二叉排序树 的第二种方法
     * @param array
     * @return
     */
    public void createBinarySortTree2(int[] array) {

        for (int i = 0; i < array.length; i++) {
            if (i == 0) {
                rootNode = new TreeNode(array[i]);
                continue;
            }

            TreeNode node = rootNode;
            while (true) {
                if (array[i] < node.getData()) {

                    if (node.getLchild() == null) {
                        node.setLchild(new TreeNode(array[i]));
                        break;
                    } else {
                        node = node.getLchild();
                    }

                } else if (array[i] == node.getData()) {
                    System.out.println("已存在" + array[i] + "，不再插入二叉排序树");
                    break;
                } else {

                    if (node.getRchild() == null) {
                        node.setRchild(new TreeNode(array[i]));
                        break;
                    } else {
                        node = node.getRchild();
                    }

                }
            }
        }

    }

    /**
     * 中序遍历
     * @param node
     */
    public void inOrderTraverse(TreeNode node) {
        if (node != null) {
            inOrderTraverse(node.getLchild());
            System.out.print(node.getData() + " ");
            inOrderTraverse(node.getRchild());
        }
    }

    /**
     * 二叉排序树的查找 （递归实现）
     *
     * 查找可以有两种实现方法，一种是递归，一种是while 循环。
     * 在插入和删除操作中也首先需要查询操作，这时使用while 循环比较好，可以知道要查询结点的双亲结点
     * @param node
     * @param key
     * @return 返回
     */
    public boolean searchBST(TreeNode node, int key) {
        if (node == null) {
            return false;
        } else if (key == node.getData()) {
            return true;
        } else if (key < node.getData()) {
            return searchBST(node.getLchild(), key);
        } else {
            return searchBST(node.getRchild(), key);
        }
    }

    //非递归查找
    public boolean iterativeSearch(TreeNode node,int key)
    {
        TreeNode tempNode=node;
        while(tempNode!=null)
        {
            if(tempNode.getData()>key)
            {
                tempNode=tempNode.getLchild();
            }
            else if(tempNode.getData()<key)
            {
                tempNode=tempNode.getRchild();
            }
            else
            {
                return true;
            }
        }
        return false;
    }

    /**
     * 二叉排序树的插入
     * @param node
     * @param key
     */
    public boolean insertBST(int key) {

        //相当于 search 用非递归实现 -----begin
        TreeNode node = rootNode;
        //查找 最后访问的 node
        TreeNode searchLastNode = null;

        while (node != null) {
            searchLastNode = node;
            if (key < node.getData()) {
                node = node.getLchild();
            } else if (key > node.getData()) {
                node = node.getRchild();
            } else {
                return false;
            }
        }
        // search ----end

        TreeNode newNode = new TreeNode(key);

        if (rootNode == null) {
            rootNode = newNode;
        } else if (key < searchLastNode.getData()) {
            searchLastNode.setLchild(newNode);
        } else {
            searchLastNode.setRchild(newNode);
        }

        return true;
    }

    public boolean deleteBST(int key) {
        //相当于 search 用非递归实现 -----begin
        TreeNode node = rootNode;
        //存储 其双亲结点，如果是根节点，则双亲结点为null
        TreeNode parentNode = null;

        while (node != null) {
            if (key < node.getData()) {
                parentNode = node;
                node = node.getLchild();
            } else if (key > node.getData()) {
                parentNode = node;
                node = node.getRchild();
            } else {
                //相等时已找到
                break ;
            }
        }

        // search ----end

        //没有找到要删除的node
        if (node == null) {
            return false;
        }

        // 右子树为空 ，重接左子树
        if (node.getRchild() == null) {
            if (parentNode != null) {
                if (parentNode.getLchild() == node)
                    parentNode.setLchild(node.getLchild());
                else
                    parentNode.setRchild(node.getLchild());
            } else {
                rootNode = node.getLchild();
            }
        // 左子树为空，重接右子树
        } else if (node.getLchild() == null) {
            if (parentNode != null) {
                if (parentNode.getLchild() == node)
                    parentNode.setLchild(node.getRchild());
                else
                    parentNode.setRchild(node.getRchild());
            } else {
                rootNode = node.getRchild();
            }
        // 左右子树都不为空 ，可以将 要删除结点 按中序遍历的前驱或后继 替代 要删除结点的位置，此处取前驱
        } else {

            //取前驱结点 ，先转左，然后一直到最右
            TreeNode replaceNode = node.getLchild();
            TreeNode replaceParentNode = node;

            if (replaceNode.getRchild() != null) {
                replaceParentNode = replaceNode;
                replaceNode = replaceNode.getRchild();
            }
            //获取到前驱结点极其双亲结点

            //如果前驱结点的双亲结点是 要删除的结点
            if (replaceParentNode == node)
                replaceParentNode.setLchild(replaceNode.getLchild());
            else
                replaceParentNode.setRchild(replaceNode.getLchild());

            node.setData(replaceNode.getData());
        }

        return true;
    }

    public static void main(String[] args) {
//        int[] array = new int[15];
//        System.out.print("随机数：");
//        for (int i = 0; i < 15; i++) {
//            array[i] = (int) (Math.random() * 100);
//            System.out.print(array[i] + " ");
//        }

        int[] array = {4, 10, 1, 13, 3, 15, 9, 11, 8, 5, 14, 2, 6, 7, 12};

        BinarySortTree binarySortTree = new BinarySortTree();
        //创建二叉排序树
        binarySortTree.createBinarySortTree1(array);

        //中序遍历 即是 从小到大的排序
        System.out.print("\n中序遍历结果：");
        binarySortTree.inOrderTraverse(binarySortTree.getRootNode());

        //二叉排序树的查找
        boolean searchResult = binarySortTree.iterativeSearch(binarySortTree.getRootNode(), 10);
        if (searchResult)
            System.out.println("\n查到");
        else
            System.out.println("\n查不到");

//        二叉排序树的删除
        binarySortTree.deleteBST(13);
        binarySortTree.inOrderTraverse(binarySortTree.getRootNode());
    }
}

class TreeNode {
    private int data;

    private TreeNode lchild;

    private TreeNode rchild;

    public TreeNode(int data) {
        this.data = data;
    }

    public int getData() {
        return data;
    }

    public void setData(int data) {
        this.data = data;
    }

    public TreeNode getLchild() {
        return lchild;
    }

    public void setLchild(TreeNode lchild) {
        this.lchild = lchild;
    }

    public TreeNode getRchild() {
        return rchild;
    }

    public void setRchild(TreeNode rchild) {
        this.rchild = rchild;
    }

    @Override
    public String toString() {
        return "TreeNode [data=" + data + ", lchild=" + lchild + ", rchild=" + rchild + "]";
    }
}

结果：

中序遍历结果：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
查到
1 2 3 4 5 6 7 8 9 10 11 12 14 15 

---

---

平衡二叉树

有空再写

https://www.cnblogs.com/skywang12345/p/3577479.html