P3813 [FJOI2017]矩阵填数

传送门

矩阵很大，但是发现 $n$ 很小，从这边考虑，对于一个一堆小矩阵放在一起的情况

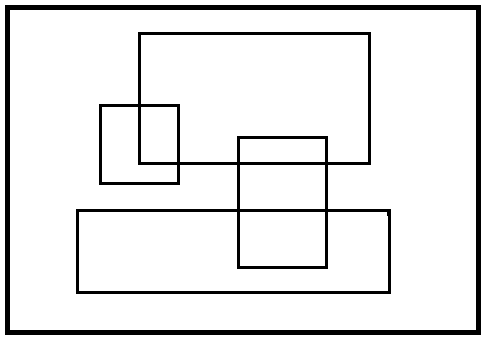
考虑把每一块单独考虑然后方案再乘起来

但是这些奇怪的东西很不好考虑

所以暴力一点，直接拆成一个个小块

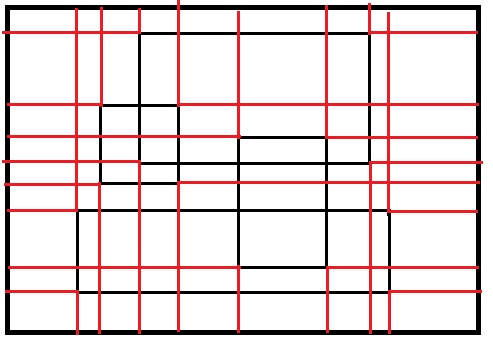
但是这样我们还要考虑到小矩形的限制，设 $f[i][S]$ 表示现在考虑完第 $i$ 个小块，小矩形的限制满足的状态为 $S$ 时的方案数

发现这些小块不会跨过矩形，维护每个小块的限制（即这个块能填的最大的数）$Mx$，以及这个小块填最大数时，能使哪些小矩形满足限制 ($P$)

设小块的面积为 $S$，那么如果下一小矩形不填最大数，则转移到 $f[i+1][S]$，贡献方案数为 $(Mx[i+1]-1)^{S[i+1]}$

如果下一小矩形填最大数，则转移到 $f[i+1][S|P[i+1]]$，贡献为总方案数-不填最大数的方案数$Mx[i+1]^{S[i+1]}\ -\ (Mx[i+1]-1)^{S[i+1]}$

然后就是奇奇怪怪的离散化和预处理了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=,mo=1e9+;
int T,h,w,n,m;
int X1[N],X2[N],Y1[N],Y2[N],v[N];
int xp[N],yp[N],tx,ty,tot;
int tmp[N],t;
int f[N][N],S[N],Mx[N],P[N];
inline bool pd(int x,int y,int k) { return x>=X1[k]&&x<=X2[k]&&y>=Y1[k]&&y<=Y2[k]; }
//判断以(x,y)右上角的小块是否在矩形k中，因为离散化后小块不可能跨过矩形所以可以这样判断
inline int ksm(int x,int y)
{
    int res=;
    while(y)
    {
        if(y&) res=1ll*res*x%mo;
        x=1ll*x*x%mo; y>>=;
    }
    return res;
}
int main()
{
    //以下默认往右为大，往上为大
    T=read();
    while(T--)
    {
        memset(f,,sizeof(f)); memset(P,,sizeof(P));
        xp[tx=]=; yp[ty=]=; tot=;
        h=read(),w=read(),m=read(),n=read();
        for(int i=;i<=n;i++)
        {
            X1[i]=read(),Y1[i]=read(),X2[i]=read(),Y2[i]=read(),v[i]=read();
            xp[++tx]=X1[i]-,yp[++ty]=Y1[i]-;//注意-1,边界很重要，左下弄成开区间很重要!
            xp[++tx]=X2[i],yp[++ty]=Y2[i];
        }
        xp[++tx]=h; yp[++ty]=w;
        sort(xp+,xp+tx+); sort(yp+,yp+ty+);
        for(int i=;i<=tx;i++) tmp[i]=xp[i]; t=tx; tx=;
        for(int i=;i<=t;i++) if(i==||tmp[i]!=tmp[i-]) xp[++tx]=tmp[i];//离散化
        for(int i=;i<=ty;i++) tmp[i]=yp[i]; t=ty; ty=;
        for(int i=;i<=t;i++) if(i==||tmp[i]!=tmp[i-]) yp[++ty]=tmp[i];//离散化
        for(int i=;i<=tx;i++)
            for(int j=;j<=ty;j++)
            {
                tot++; Mx[tot]=m;
                S[tot]=(xp[i]-xp[i-])*(yp[j]-yp[j-]);//小的边界是不包含的，即区间是左开右闭的，下开上闭的
                for(int k=;k<=n;k++)
                    if(pd(xp[i],yp[j],k)) Mx[tot]=min(Mx[tot],v[k]);//处理Mx
                for(int k=;k<=n;k++)
                    if(pd(xp[i],yp[j],k) && Mx[tot]==v[k])//处理P
                        P[tot]|=(<<k-);
            }
        int mx=(<<n)-; f[][]=;//DP
        for(int i=;i<tot;i++)
        {
            int t1=ksm(Mx[i+]-,S[i+]),t2=(ksm(Mx[i+],S[i+])-t1+mo)%mo;
            for(int j=;j<=mx;j++)
            {
                if(!f[i][j]) continue;
                f[i+][j|P[i+]]=(f[i+][j|P[i+]]+1ll*f[i][j]*t2%mo)%mo;//此块填最大数
                f[i+][j]=(f[i+][j]+1ll*f[i][j]*t1%mo)%mo;//此块不填最大数
            }
        }
        printf("%d\n",f[tot][mx]);
    }
}