UVA766 Sum of powers(1到n的自然数幂和 伯努利数)

自然数幂和：

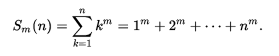
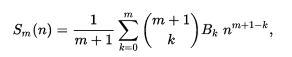(1)

伯努利数的递推式：

B0 = 1

(要满足(1)式,求出Bn后将B1改为1 /2)

参考：https://en.wikipedia.org/wiki/Bernoulli_number

http://blog.csdn.net/acdreamers/article/details/38929067

使用分数类，代入求解

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
#include<utility>
using namespace std;
typedef long long LL;
const int N = 25, INF = 0x3F3F3F3F;

LL gcd(LL a, LL b){
    while(b){
        LL t = a % b;
        a = b;
        b = t;
    }
    return a;
}

LL lcm(LL a, LL b){
    return a / gcd(a, b) * b;
}

struct frac{
	LL x, y;
	frac(){
		x = 0;
		y = 1;
	}
	frac(LL x1, LL y1){
		x = x1;
		y = y1;
	}
	frac operator*(const frac &tp)const{
		LL a = x * tp.x;
		LL b = y * tp.y;
		LL d = gcd(a, b);
		a /= d;
		b /= d;
		if(a >= 0 && b < 0){
            a = -a;
            b = -b;
		}
		return frac(a, b);
	}

	frac operator+(const frac &tp)const{
		LL a = x * tp.y + tp.x * y;
		LL b = y * tp.y;
		LL d = gcd(a, b);
		a /= d;
		b /= d;
		if(a >= 0 && b < 0){
            a = -a;
            b = -b;
		}

		return frac(a, b);
	}

}ans[N][N], bo[N];

LL cm[N][N];
void init(){
	memset(cm, 0, sizeof(cm));
	cm[0][0] = 1;
	for(int i = 1; i < N; i++){
		cm[i][0] = 1;
		for(int j = 1; j <= i; j++){
			cm[i][j] = cm[i - 1][j - 1] + cm[i - 1][j];
		}
	}

	bo[0].x = 1, bo[0].y = 1;
	for(int i = 1; i < N; i++){
		bo[i].x = 0;
		bo[i].y = 1;
		for(int j = 0; j < i; j++){
			bo[i] = bo[i] + frac(cm[i + 1][j], 1) * bo[j];
		}
		bo[i] = bo[i] * frac(-1, i + 1);
	}
	bo[1].x = 1; bo[1].y = 2;
	for(int m = 0; m < N; m++){
		for(int k = 0; k <= m; k++){
			ans[m][m + 1 - k] = frac(cm[m + 1][k], 1) * bo[k] * frac(1, m + 1);
		}
		LL lc = ans[m][0].y;
		for(int k = 1; k <= m; k++){
			lc = lcm(ans[m][k].y, lc);
		}
		for(int k = 0; k <= m + 1; k++){
            LL d = lc / ans[m][k].y;
            ans[m][k].x *= d;
            ans[m][k].y *= d;
		}
	}

}

int main(){
    init();
    int t;
    cin >> t;
    while(t--){
    	int n;
    	cin >>n;
    	printf("%lld ", ans[n][0].y);
    	for(int i = n + 1; i >= 0; i--){
    		if(i == 0){
    			printf("%lld\n", ans[n][i].x);
    		}else{
    			printf("%lld ", ans[n][i].x);
    		}
    	}
        if(t){
            printf("\n");
        }
    }

    return 0;
}