算法导论-顺序统计-快速求第i小的元素
目录
1、问题的引出-求第i个顺序统计量
2、方法一：以期望线性时间做选择
3、方法二（改进）：最坏情况线性时间的选择
4、完整测试代码（c++）
5、参考资料
内容
1、问题的引出-求第i个顺序统计量
什么是顺序统计量？及中位数概念
在一个由元素组成的集合里，第i个顺序统计量（order statistic）是该集合第i小的元素。例如，最小值是第1个顺序统计量(i=1)，最大值是第n个顺序统计量(i=n)。一个中位数（median）是它所在集合的“中点元素”。当n为奇数时，中位数是唯一的；当n为偶数时，中位数有两个。问题简单的说就是：求数组中第i小的元素。
那么问题来了：如何求一个数组里第i小的元素呢？
常规方法：可以首先进行排序，然后取出中位数。由于排序算法（快排，堆排序，归并排序）效率能做到Θ(nlogn),所以，效率达不到线性； 在本文中将介绍两种线性的算法，第一种期望效率是线性的，第二种效率较好，是在最坏情况下能做到线性效率。见下面两个小节；
2、方法一：以期望线性时间做选择
这是一种分治算法：以快速排序为模型：随机选取一个主元，把数组划分为两部分，A[p...q-1]的元素比A[q]小，A[q+1...r]的元素比A[q]大。与快速排序不同，如果i=q，则A[q]就是要找的第i小 的元素，返回这个值；如果i < q，则说明第i小的元素在A[p...q-1]里；如果i > q，则说明第i小的元素在A[q+1...r]里；然后在上面得到的高区间或者低区间里进行递归求取，直到找到第i小的元素。
下面是在A[p...q]中找到第i小元素的伪码：
RandomSelect(A,p, q,k)//随机选择统计，以期望线性时间做选择
{
if (p==q) return A[p];
int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
int i=pivot-p+;
if (i==k )return A[pivot];
else if (i<k) return RandomSelect(A,pivot+,q,k-i);//第k小的数不在主元左边，则在右边递归选择
else return RandomSelect(A,p,pivot-,k);//第k小的数不在主元右边，则在左边递归选择
}
在最坏情况下，数组被划分为n-1和0两部分，而第i个元素总是落在n-1的那部分里，运行时间为Ө(n^2);但是，除了上述很小的概率情况，其他情况都能达到线性；在平均情况下，任何顺序统计量都可以在线性时间Θ(n)内得到。
实现代码（c++）：
//template<typename T>使用模板，可处理任意类型的数据
template<typename T>//交换数据
void Swap(T &m,T &n)
{
T tmp;
tmp=m;
m=n;
n=tmp;
} /***********随机快速排序分划程序*************/
template<typename T>
int Random_Partition(vector<T> &A,int p,int q)
{
//随机选择主元，与第一个元素交换
srand(time(NULL));
int m=rand()%(q-p+)+p;
Swap(A[m],A[p]);
//下面与常规快排划分一样
T x=A[p];
int i=p;
for (int j=p+;j<=q;j++)
{
if (A[j]<x)
{
i=i+;
Swap(A[i],A[j]);
}
}
Swap(A[p],A[i]);
return i;
}
/***********随机选择统计函数*************/
template<typename T>
T RandomSelect(vector<T> &A,int p,int q,int k)//随机选择统计，以期望线性时间做选择
{
if (p==q) return A[p];
int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
int i=pivot-p+;
if (i==k )return A[pivot];
else if (i<k) return RandomSelect(A,pivot+,q,k-i);//第k小的数不在主元左边，则在右边递归选择
else return RandomSelect(A,p,pivot-,k);//第k小的数不在主元右边，则在左边递归选择
}
3、方法二（改进）：最坏情况线性时间的选择
相比于上面的随机选择，我们有另一种类似的算法，它在最坏情况下也能达到O(n)。它也是基于数组的划分操作，而且利用特殊的手段保证每次划分两边的子数组都比较平衡；与上面算法不同之处是：本算法不是随机选择主元，而是采取一种特殊的方法选择“中位数”，这样能使子数组比较平衡，避免了上述的最坏情况（Ө(n^2)）。选出主元后，后面的处理和上述算法一致。
那么问题又来了，这种特殊的手段是什么呢？
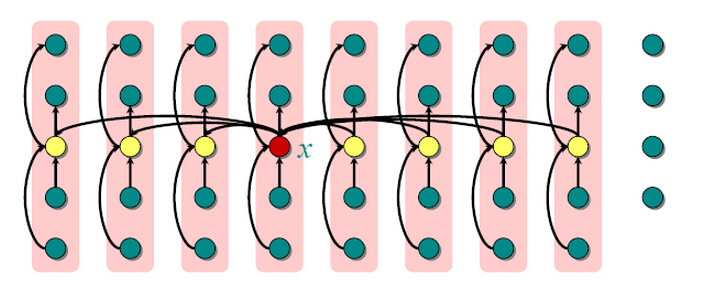
如上图所示：
1） 将输入数组的n个元素划分为n/5组，每组（上图中的每列为一组）5个元素，且至多只有一个组有剩下的n%5个元素组成
2） 首先对每组中的元素（5个）进行插入排序，然后从排序后的序列中选择出中位数（图中黄色数）。
3） 对第2步中找出的n/5个中位数，递归调用SELECT以找出其中位数x（图中红色数）。（如果有偶数个中位数取较小的中位数）
这三个步骤就可以选出一个很好的主元，下面的处理和方法一一致（递归）
OK! 下面是完整的算法步骤：
1） 将输入数组的n个元素划分为n/5组，每组（上图中的每列为一组）5个元素，且至多只有一个组有剩下的n%5个元素组成
2） 首先对每组中的元素（5个）进行插入排序，然后从排序后的序列中选择出中位数（图中黄色数）。
3） 对第2步中找出的n/5个中位数，递归调用SELECT以找出其中位数x（图中红色数）。（如果有偶数个中位数取较小的中位数）
4） 调用PARTITION过程，按照中位数x对输入数组进行划分。确定中位数x的位置k。
5） 如果i=k，则返回x。否则，如果i<k，则在地区间递归调用SELECT以找出第i小的元素，若干i>k，则在高区找第(i-k)个最小元素。
大致伪码：
WorseLinearSelect(vector<T> &A,int p,int q,int k)
{
// 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
// 且至多只有一个组有剩下的n%5个元素组成。
if (p==q) return A[p]; int len=q-p+;
int medianCount=;
if (len>)
medianCount = len% > ? len/ + : len/;
vector<T> medians(medianCount);//存放每组的中位数 // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
// 然后从排序后的序列中选择出中位数。
int m=p;
for (int j=,m=p;j<medianCount-;j++)
{
medians[j] = GetMedian(A,m,m+);
m+=;
}
medians[medianCount-] = GetMedian(A,m,q);
//对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
//（如果是偶数去下中位数）
int pivot = WorseLinearSelect(medians,,medianCount-,(medianCount+)/);
//调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
int r = partitionWithPivot(A,p,q,pivot);
int num = r-p+;
//如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
//若干k>num，则在高区找第(k-num)个最小元素。
if(num==k) return pivot;
else if (num>k) return WorseLinearSelect(A,p,r-,k);
else return WorseLinearSelect(A,r+,q,k-num);
}
该算法在最坏情况下运行时间为Θ(n)
代码实现(c++)：
template<typename T>//插入排序
void insertion_sort(vector<T> &A,int p,int q)
{
int i,j;
T key;
int len=q-p+;
for (j=p+;j<=q;j++)
{
i=j-;
key=A[j];
while (i>=p&&A[i]>key)
{
A[i+]=A[i];
i--;
}
A[i+]=key;
}
}
/*
* 利用插入排序选择中位数
*/
template<typename T>
T GetMedian(vector<T> &A,int p,int q)
{
insertion_sort(A,p,q);//插入排序
return A[(q-p)/ + p];//返回中位数,有两个中位数的话返回较小的那个
}
/*
* 根据指定的划分主元pivot来划分数组
* 并返回主元的顺序位置
*/
template<typename T>
int partitionWithPivot(vector<T> &A,int p,int q,T piovt)
{
//先把主元交换到数组首元素
for (int i=p;i<q;i++)
{
if (A[i] == piovt)
{
Swap(A[i],A[p]);
break;
}
}
//常规的快速排序划分程序
//
T x=A[p];
int i=p;
for (int j=p+;j<=q;j++)
{
if (A[j]<x)
{
i=i+;
Swap(A[i],A[j]);
}
}
Swap(A[p],A[i]);
return i;
}
/*
* 最坏情况下线性时间选择算法
* 此算法依然是建立在快速排序的划分算法基础之上的
* 但是与randomizedSelect算法的不同指之处，就是次算法的本质
* 是保证了每次划分选择的划分主元一定是一个较好的主元，算法先对数组5个一组进行分组
* 然后选择每组的中位数，再递归的选择各组中位数中的中位数作为数组的划分主元，以此保证划分的平衡性
* 选择中位数的时候必须使用递归调用的方法才能降低时间复杂度
* 从而保证在最坏情况下都得到一个好的划分
* 最坏情况下时间复杂度为O(n)
*/
template<typename T>
T WorseLinearSelect(vector<T> &A,int p,int q,int k)
{
// 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
// 且至多只有一个组有剩下的n%5个元素组成。
if (p==q) return A[p]; int len=q-p+;
int medianCount=;
if (len>)
medianCount = len% > ? len/ + : len/;
vector<T> medians(medianCount);//存放每组的中位数 // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
// 然后从排序后的序列中选择出中位数。
int m=p;
for (int j=,m=p;j<medianCount-;j++)
{
medians[j] = GetMedian(A,m,m+);
m+=;
}
medians[medianCount-] = GetMedian(A,m,q);
//对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
//（如果是偶数去下中位数）
int pivot = WorseLinearSelect(medians,,medianCount-,(medianCount+)/);
//调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
int r = partitionWithPivot(A,p,q,pivot);
int num = r-p+;
//如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
//若干k>num，则在高区找第(k-num)个最小元素。
if(num==k) return pivot;
else if (num>k) return WorseLinearSelect(A,p,r-,k);
else return WorseLinearSelect(A,r+,q,k-num);
}
4、完整测试代码（c++）
Select.h
#ifndef SELECT_HH
#define SELECT_HH
template<typename T>
class Select
{
public:
T RandomSelect(vector<T> &A,int p,int q,int k);//期望线性时间做选择
T WorseLinearSelect(vector<T> &A,int p,int q,int k);//最坏情况线性时间的选择
private:
void Swap(T &m,T &n);//交换数据
int Random_Partition(vector<T> &A,int p,int q);//随机快排分划
void insertion_sort(vector<T> &A,int p,int q);//插入排序
T GetMedian(vector<T> &A,int p,int q);
int partitionWithPivot(vector<T> &A,int p,int q,T piovt);//根据指定主元pivot来划分数据并返回主元的顺序位置
}; template<typename T>//交换数据
void Select<T>::Swap(T &m,T &n)
{
T tmp;
tmp=m;
m=n;
n=tmp;
} /***********随机快速排序分划程序*************/
template<typename T>
int Select<T>::Random_Partition(vector<T> &A,int p,int q)
{
//随机选择主元，与第一个元素交换
srand(time(NULL));
int m=rand()%(q-p+)+p;
Swap(A[m],A[p]);
//下面与常规快排划分一样
T x=A[p];
int i=p;
for (int j=p+;j<=q;j++)
{
if (A[j]<x)
{
i=i+;
Swap(A[i],A[j]);
}
}
Swap(A[p],A[i]);
return i;
}
/***********随机选择统计函数*************/
template<typename T>
T Select<T>::RandomSelect(vector<T> &A,int p,int q,int k)//随机选择统计，以期望线性时间做选择
{
if (p==q) return A[p];
int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
int i=pivot-p+;
if (i==k )return A[pivot];
else if (i<k) return RandomSelect(A,pivot+,q,k-i);//第k小的数不在主元左边，则在右边递归选择
else return RandomSelect(A,p,pivot-,k);//第k小的数不在主元右边，则在左边递归选择
} template<typename T>//插入排序
void Select<T>::insertion_sort(vector<T> &A,int p,int q)
{
int i,j;
T key;
int len=q-p+;
for (j=p+;j<=q;j++)
{
i=j-;
key=A[j];
while (i>=p&&A[i]>key)
{
A[i+]=A[i];
i--;
}
A[i+]=key;
}
}
/*
* 利用插入排序选择中位数
*/
template<typename T>
T Select<T>::GetMedian(vector<T> &A,int p,int q)
{
insertion_sort(A,p,q);//插入排序
return A[(q-p)/ + p];//返回中位数,有两个中位数的话返回较小的那个
}
/*
* 根据指定的划分主元pivot来划分数组
* 并返回主元的顺序位置
*/
template<typename T>
int Select<T>::partitionWithPivot(vector<T> &A,int p,int q,T piovt)
{
//先把主元交换到数组首元素
for (int i=p;i<q;i++)
{
if (A[i] == piovt)
{
Swap(A[i],A[p]);
break;
}
}
//常规的快速排序划分程序
//
T x=A[p];
int i=p;
for (int j=p+;j<=q;j++)
{
if (A[j]<x)
{
i=i+;
Swap(A[i],A[j]);
}
}
Swap(A[p],A[i]);
return i;
}
/*
* 最坏情况下线性时间选择算法
* 此算法依然是建立在快速排序的划分算法基础之上的
* 但是与randomizedSelect算法的不同指之处，就是次算法的本质
* 是保证了每次划分选择的划分主元一定是一个较好的主元，算法先对数组5个一组进行分组
* 然后选择每组的中位数，再递归的选择各组中位数中的中位数作为数组的划分主元，以此保证划分的平衡性
* 选择中位数的时候必须使用递归调用的方法才能降低时间复杂度
* 从而保证在最坏情况下都得到一个好的划分
* 最坏情况下时间复杂度为O(n)
*/
template<typename T>
T Select<T>::WorseLinearSelect(vector<T> &A,int p,int q,int k)
{
// 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
// 且至多只有一个组有剩下的n%5个元素组成。
if (p==q) return A[p]; int len=q-p+;
int medianCount=;
if (len>)
medianCount = len% > ? len/ + : len/;
vector<T> medians(medianCount);//存放每组的中位数 // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
// 然后从排序后的序列中选择出中位数。
int m=p;
for (int j=,m=p;j<medianCount-;j++)
{
medians[j] = GetMedian(A,m,m+);
m+=;
}
medians[medianCount-] = GetMedian(A,m,q);
//对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
//（如果是偶数去下中位数）
int pivot = WorseLinearSelect(medians,,medianCount-,(medianCount+)/);
//调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
int r = partitionWithPivot(A,p,q,pivot);
int num = r-p+;
//如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
//若干k>num，则在高区找第(k-num)个最小元素。
if(num==k) return pivot;
else if (num>k) return WorseLinearSelect(A,p,r-,k);
else return WorseLinearSelect(A,r+,q,k-num);
}
#endif
main.cpp
#include <iostream>
#include <vector>
#include <time.h>
using namespace std;
#include "Select.h"
#define N 10 //排序数组大小
#define K 100 //排序数组范围0～K
////打印数组
void print_element(vector<int> A)
{
int len=A.size();
for (int i=;i<len;i++)
{
std::cout<<A[i]<<" ";
}
std::cout<<std::endl;
}
int main()
{
Select <int> s1;
int a[]={,,,,,,,,,};
vector<int> vec_int(a,a+);
cout<<"原始数组"<<endl;
print_element(vec_int);
// 期望线性时间做选择测试
cout<<"期望线性时间做选择测试"<<endl;
for(int i=;i<=N;i++)
{
int kMin=s1.RandomSelect(vec_int,,N-,i);
cout<<"第"<<i<<"小的数是："<<kMin<<endl;
}
//最坏情况线性时间的选择测试
cout<<"最坏情况线性时间的选择测试"<<endl;
for(int i=;i<=N;i++)
{
int kMin=s1.WorseLinearSelect(vec_int,,N-,i);
cout<<"第"<<i<<"小的数是："<<kMin<<endl;
}
system("PAUSE");
return ;
}
5、参考资料
【1】http://blog.csdn.net/xyd0512/article/details/8279371
【2】http://blog.chinaunix.net/uid-26822401-id-3163058.html
【3】http://www.tuicool.com/articles/mqQBfm
【4】http://www.cnblogs.com/Anker/archive/2013/01/25/2877311.html
算法导论-顺序统计-快速求第i小的元素的更多相关文章
- 树状数组求第k小的元素
int find_kth(int k) { int ans = 0,cnt = 0; for (int i = 20;i >= 0;i--) //这里的20适当的取值,与MAX_VAL有关,一般 ...
- 利用快排partition求前N小的元素
求前k小的数,一般人的想法就是先排序,然后再遍历,但是题目只是求前N小,没有必要完全排序,所以可以想到部分排序,而能够部分排序的排序算法我能想到的就是堆排序和快排了. 第一种思路,局部堆排序. 首先, ...
- [算法导论]练习2-4.d求排列中逆序对的数量
转载请注明:http://www.cnblogs.com/StartoverX/p/4283186.html 题目:给出一个确定在n个不同元素的任何排列中逆序对数量的算法,最坏情况需要Θ(nlgn)时 ...
- 算法打基础——顺序统计(找第k小数)
这次主要是讲如何在线性时间下找n个元素的未排序序列中第k小的数.当然如果\(k=1 or k=n\),即找最大最小 数,线性时间内遍历即可完成,当拓展到一般,如中位数时,相关算法就值得研究了.这里还要 ...
- 315. Count of Smaller Numbers After Self(二分或者算法导论中的归并求逆序数对)
You are given an integer array nums and you have to return a new counts array. The counts array has ...
- 求第k小的元素
用快排解决: 用快排,一趟排序后,根据基准值来缩小问题规模.基准值的下角标i 加1 表示了基准值在数组中第几小.如果k<i+1,那就在左半边找:如果k>i+1那就在右半边找.当基准值的下角 ...
- 求第 k 小:大元素
#include<bits/stdc++.h> using namespace std; void swap_t(int a[],int i,int j) { int t=a[i]; a[ ...
- 《算法导论》— Chapter 9 中位数和顺序统计学
序 在算法导论的第二部分主要探讨了排序和顺序统计学,第六章~第八章讨论了堆排序.快速排序以及三种线性排序算法.该部分的最后一个章节,将讨论顺序统计方面的知识. 在一个由n个元素组成的集合中,第i个顺序 ...
- 算法导论学习之线性时间求第k小元素+堆思想求前k大元素
对于曾经,假设要我求第k小元素.或者是求前k大元素,我可能会将元素先排序,然后就直接求出来了,可是如今有了更好的思路. 一.线性时间内求第k小元素 这个算法又是一个基于分治思想的算法. 其详细的分治思 ...
随机推荐
- python学习笔记 可变参数关键字参数**kw相关学习
在Python中可以定义可变参数,顾名思义,可变参数就是传入参数是可变的.可以是任意个,以一个简单的数学编程为例,计算 sum = a * a + b * b + .....z * z 函数定义可以如 ...
- P1489 猫狗大战
P1489 猫狗大战 题目描述 新一年度的猫狗大战通过SC(星际争霸)这款经典的游戏来较量,野猫和飞狗这对冤家为此已经准备好久了,为了使战争更有难度和戏剧性,双方约定只能选择Terran(人族)并且只 ...
- django自带的orm之查询
一.filter条件查询 用法: 模型类.objects.filter(模型类属性名__查询操作符 = 值) 判等: exact # 例:查询id为1的员工 select * from employe ...
- Python与Mysql交互
#转载请联系 在写内容之前,先放一张图,bling- 这张图算是比较详细的表达出了web开发都需要什么.用户访问网页,就是访问服务器的网页文件.这些网页文件由前端工程师编写的.服务器通常用nginx/ ...
- TCP 粘包及其解决方案(zz)
首先,我们回顾一下 TCP 和 UDP 的头部信息: 具体说明看:http://www.cnblogs.com/aomi/p/7776582.html 我们知道,TCP 和 UDP 是 TCP/IP ...
- c#读取LOG文件并解决读取提示被其他进程占用问题
c# 读写文件时文件正由另一进程使用,因此该进程无法访问该文件,在IO处理上遇到了无法操作的问题. 文件“C:\u_ex.log”正由另一进程使用,因此该进程无法访问该文件. u_ex.log是一个日 ...
- 【转】requests、BeautifulSoup使用总结
转自,https://www.cnblogs.com/wupeiqi/articles/6283017.html ---- Python标准库中提供了:urllib.urllib2.httplib等 ...
- mysql having的用法
having的用法 having字句可以让我们筛选成组后的各种数据,where字句在聚合前先筛选记录,也就是说作用在group by和having字句前.而 having子句在聚合后对组记录进行筛选. ...
- 洛谷 P2678 跳石头【经典二分答案/贪心】
题目描述 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石.组委会已经选择好了两块岩石作为比赛起点和终点.在起点和终点之间,有 NN 块岩石(不含起点和终点的岩石).在比赛过程中,选手们将从 ...
- POJ 2387 链式前向星下的SPFA
(POJ)[http://poj.org/problem?id=2387] Til the Cows Come Home Time Limit: 1000MS Memory Limit: 65536K ...