C / C ++ 基于梯度下降法的线性回归法（适用于机器学习）

写在前面的话：

在第一学期做项目的时候用到过相应的知识，觉得挺有趣的，就记录整理了下来，基于C/C++语言

原贴地址：https://helloacm.com/cc-linear-regression-tutorial-using-gradient-descent/

---------------------------------------------------------------前言----------------------------------------------------------------------------------

在机器学习和数据挖掘处理等领域，梯度下降（Gradient Descent）是一种线性的、简单却比较有效的预测算法。它可以基于大量已知数据进行预测，　并可以通过控制误差率来确定误差范围。

--------------------------------------------------------准备------------------------------------------------------------------------

Gradient Descent

回到主题，线性回归算法有很多，但Gradient Descent是最简单的方法之一。对于线性回归，先假设数据满足线性关系，例如：

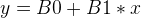
所以，作为线性回归，我们的任务就是找到最合适 B0 和 B1， 使最后的结果Y满足可接受的准确度。作为起步，首先让我们对B0和B1赋值初始值0，如下所示：

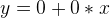
设误差 Error 为 e， 并引入下面几个点做例子：

x y

如果我们计算第一个点的误差，则得到 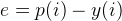，其中P（i）为表中的数据值，则 e 结果为  -1。但这只是开始，下面我们可以使用Gradient Descent来更新Y中的系数。这就涉及到数据 / 机器学习， 所谓的 数据 / 机器学习，其实可以大致理解为在相应的函数模型下，通过不停地更新其中系数，使新函数曲线可以拟合原始数据并预测走势的过程。

回到主题，设刚才的初始状态为 t ，那么对于下一个状态 t+1 ， B0可表示为 ：

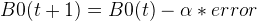
其中 B0（t + 1）是系数的更新版本，为套入下一个点做准备。∂ 是学习率，即为精度，这个我们可以自己设定。∂ 越大，说明每次学习的跨度就越大，预测结果在相应的正确答案两边的摆幅也就越大，所以此情况下学习次数不易过多，否则越摆越离谱。Ps:有次因为∂ 值太大的原因导致结果不精准，结过以为是学习次数不够多，后来等到把2.3的数值摆到10个亿才反应过来是∂出来问题。话说10个亿真是个小目标呢。

言归正传，这里取 ∂ = 0.01，即可得以下式子，B0=0.01.

.

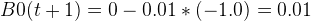现在再来看 B1，在 t+1时刻，公式变为：

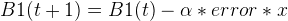
同样赋值，也同样得到：

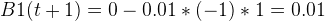
--------------------------------------------------------操作------------------------------------------------------------------------

现在，我们可以重复迭代这种过程到下一个点，再到下下个点，一直到所有点结束，这称为1回（an epoch）。但是我们可以通过反复不停地迭代，来使得到的线性拟合曲线更接近初始数据。比如迭代4回，每回5个点，也就是20次。C / C ++代码如下：

double x[] = {, , , , };
double y[] = {, , , , };

double b0 = ;
double b1 = ;
double alpha = 0.01;

for (int i = ; i < ; i ++) {
    int idx = i % ; //5个点
    double p = b0 + b1 * x[idx];
    double err = p - y[idx];
    b0 = b0 - alpha * err;
    b1 = b1 - alpha * err * x[idx];
}

把B0、B1还有 误差（Error）的结果打印出来：

B0 = 0.01, B1 = 0.01, err = -
B0 = 0.0397, B1 = 0.0694, err = -2.97
B0 = 0.066527, B1 = 0.176708, err = -2.6827
B0 = 0.0805605, B1 = 0.218808, err = -1.40335
B0 = 0.118814, B1 = 0.410078, err = -3.8254
B0 = 0.123526, B1 = 0.414789, err = -0.471107
B0 = 0.143994, B1 = 0.455727, err = -2.0469
B0 = 0.154325, B1 = 0.497051, err = -1.0331
B0 = 0.157871, B1 = 0.507687, err = -0.354521
B0 = 0.180908, B1 = 0.622872, err = -2.3037
B0 = 0.18287, B1 = 0.624834, err = -0.196221
B0 = 0.198544, B1 = 0.656183, err = -1.56746
B0 = 0.200312, B1 = 0.663252, err = -0.176723
B0 = 0.198411, B1 = 0.65755, err = 0.190068
B0 = 0.213549, B1 = 0.733242, err = -1.51384
B0 = 0.214081, B1 = 0.733774, err = -0.0532087
B0 = 0.227265, B1 = 0.760141, err = -1.31837
B0 = 0.224587, B1 = 0.749428, err = 0.267831
B0 = 0.219858, B1 = 0.735242, err = 0.472871
B0 = 0.230897, B1 = 0.790439, err = -1.10393

怎么样，能发现什么？不容易看出来没关系，我们把点画下来：

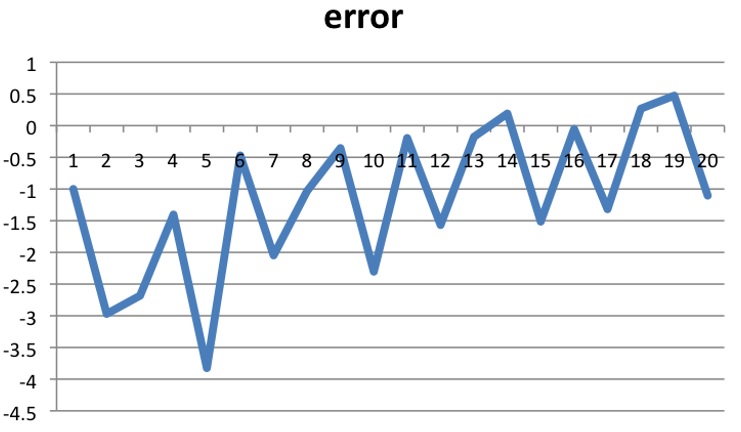
从图中，我们可以看到误差正逐渐变小，所以我们的最终模型也就是第20次的模型：

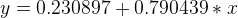
所以最后的曲线拟合结果如下：

到这里其实不一定死板地局限于20次，也并不是迭代次数越多越好，因为这个过程像一个开口向下的二次函数， 适合的才是最好的。

因为最合适的点可能就在中间，迭代太多次就跑偏了。解决这个问题可以在源代码里简单地加一个 If () 函数，当误差满足xxx时跳出循环就完事了。

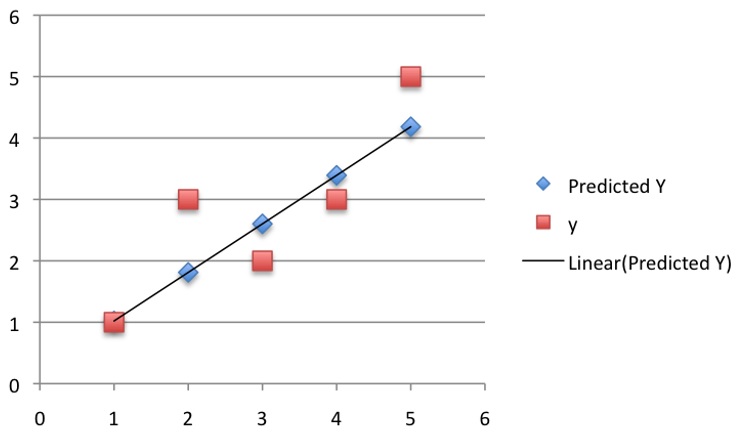
到这里应该就结束了。但原文章里多算了一次 Root-Mean-Square 值，也就是均方根，常用来分析噪声或者误差，公式如下：

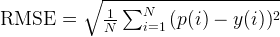   把每个点带入，得到RMSE=0.72。

--------------------------------------------------------总结------------------------------------------------------------------------

其实Gradient Descent 通常适用于 量非常大且繁琐的数据（不在乎有那么几个因为跑偏而被淘汰的值）。

但如果要求数据足够精确、且数据模型复杂，不适合一次函数模型，那Gradient Descent  并不见得是一个好方法。