[HDU5739]Fantasia(圆方树DP)

题意：给一张无向点带有权无向图。定义连通图的权值为图中各点权的乘积，图的权值为其包含的各连通图的权和。设z_i为删除i点后图的权值，求$S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$。

显然和点双有关。回忆各种tarjan：缩SCC得DAG，缩边BCC得一棵树，我们要想办法把点BCC也缩成一棵树。

tarjan求点双，然后给每个点双新建一个点，将这个BCC内的所有点连向这个点。

因为点与点之间没有边，SCC与SCC之间没有边，所以可以证明这是一棵树。这个算法有个名字叫Block Forest Data Structure.

缩成树之后随便选一个SCC点作为根，显然所有非叶子点都是割点（SCC虚拟点除外），叶子则都是非割点。

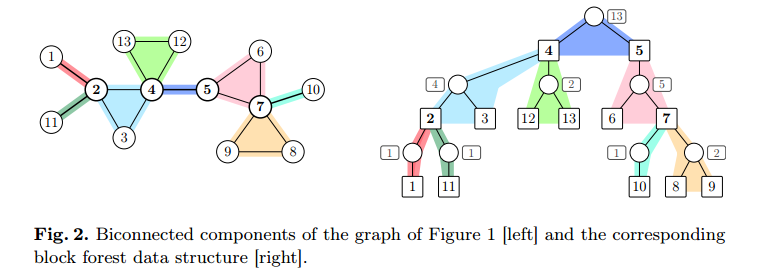
在这棵树上直接DP即可，为了方便计算直接将SCC点权赋为1。

接着是一些注意点：

　　1. 孤立点要特殊处理，因为一个点不是点双。

　　2. 缩点后的点的个数可能达到$2n$。

　　3. 当前点为割点的判定：low[k]>=dfn[x]而不是low[x]==dfn[x]，且这里要保证在此之前k未被访问过，具体看代码。

　　4. tarjan弹栈的时候要注意，弹到k为止，x特殊处理。因为x和k在栈中可能不是连续的。

UPD：才知道这个就是圆方树。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define mem(a) memset(a,0,sizeof(a))
 #define rep(i,l,r) for (int i=(l),_=(r); i<=_; i++)
 #define For(i,x) for (int i=h[x],k; i; i=nxt[i])
 using namespace std;
 
 const int N=,mod=;
 int T,n,m,tot,top,u,v,S,tim,bcc,d[N];
 int w[N],p[N],val[N],ans[N],stk[N],low[N],dfn[N],bel[N];
 bool vis[N];
 inline void up(int &x,int y){ x+=y; if (x>=mod) x-=mod; }
 
 int ksm(int a,int b){
     int res=;
     for (; b; a=1ll*a*a%mod,b>>=)
         if (b&) res=1ll*res*a%mod;
     return res;
 }
 
 struct E{
     int cnt,h[N],to[N<<],nxt[N<<];
     void add(int u,int v){ to[++cnt]=v; nxt[cnt]=h[u]; h[u]=cnt; }
 
     void dfs(int x,int fa){
         vis[x]=; val[x]=w[x]; bel[x]=tot;
         For(i,x) if ((k=to[i])!=fa)
             dfs(k,x),val[x]=1ll*val[x]*val[k]%mod;
     }
 
     void DP(int x,int fa){
         vis[x]=; ans[x]=(S-p[bel[x]]+mod)%mod;
         For(i,x) if ((k=to[i])!=fa) DP(k,x),up(ans[x],val[k]);
         up(ans[x],1ll*p[bel[x]]*ksm(val[x],mod-)%mod);
     }
 }G,G1;
 
 void tarjan(int x,int fa){
     dfn[x]=low[x]=++tim; stk[++top]=x;
     for (int i=G.h[x],k; i; i=G.nxt[i]) if ((k=G.to[i])!=fa){
         if (dfn[k]) low[x]=min(low[x],dfn[k]);
         else{
             tarjan(k,x),low[x]=min(low[x],low[k]);
             if (low[k]>=dfn[x]){
                 bcc++; w[n+bcc]=; int t;
                 while (){
                     t=stk[top]; //printf("%d %d\n",t,n+bcc);
                     G1.add(t,n+bcc); G1.add(n+bcc,t);
                     top--; if (t==k) break;
                 }
                 G1.add(x,n+bcc); G1.add(n+bcc,x);
             }
         }
     }
 }
 
 void init(){ rep(i,,n+bcc) G.h[i]=G1.h[i]=dfn[i]=d[i]=vis[i]=; G.cnt=G1.cnt=tot=top=tim=bcc=S=; }
 
 int main(){
     freopen("hdu5739.in","r",stdin);
     freopen("hdu5739.out","w",stdout);
     for (scanf("%d",&T); T--; init()){
         scanf("%d%d",&n,&m);
         rep(i,,n) scanf("%d",&w[i]);
         rep(i,,m) scanf("%d%d",&u,&v),G.add(u,v),G.add(v,u),d[u]++,d[v]++;
         rep(i,,n) if (!dfn[i]) tarjan(i,);
         rep(i,n+,n+bcc) if (!vis[i]) tot++,G1.dfs(i,),p[tot]=val[i],up(S,p[tot]);
         rep(i,,n) if (!d[i]) up(S,w[i]);
         rep(i,,n) if (!d[i]) ans[i]=(S-w[i]+mod)%mod;
         //rep(i,1,n+bcc) printf("%d ",val[i]); puts("");
         rep(i,,n+bcc) vis[i]=;
         rep(i,n+,n+bcc) if (!vis[i]) G1.DP(i,);
         //rep(i,1,n) printf("%d ",ans[i]); puts("");
         int res=;
         rep(i,,n) up(res,1ll*i*ans[i]%mod);
         printf("%d\n",res);
     }
     return ;
 }