集成方法 Ensemble

一、bagging

用于基础模型复杂、容易过拟合的情况，用来减小 variance（比如决策树）。基础模型之间没有太多联系（相对于boosting），训练可以并行。但用 bagging 并不能有助于把数据拟合的更准（那是要减小 bias）。

每次训练一个基础模型，都从 N 条训练数据中有放回的随机抽取出 N' 条作为训练集（虽然一般 N = N'，但由于是有放回的抽，所以具体的数据还是不同的）。

模型做预测的时候用 average（回归）或者 voting（分类）。

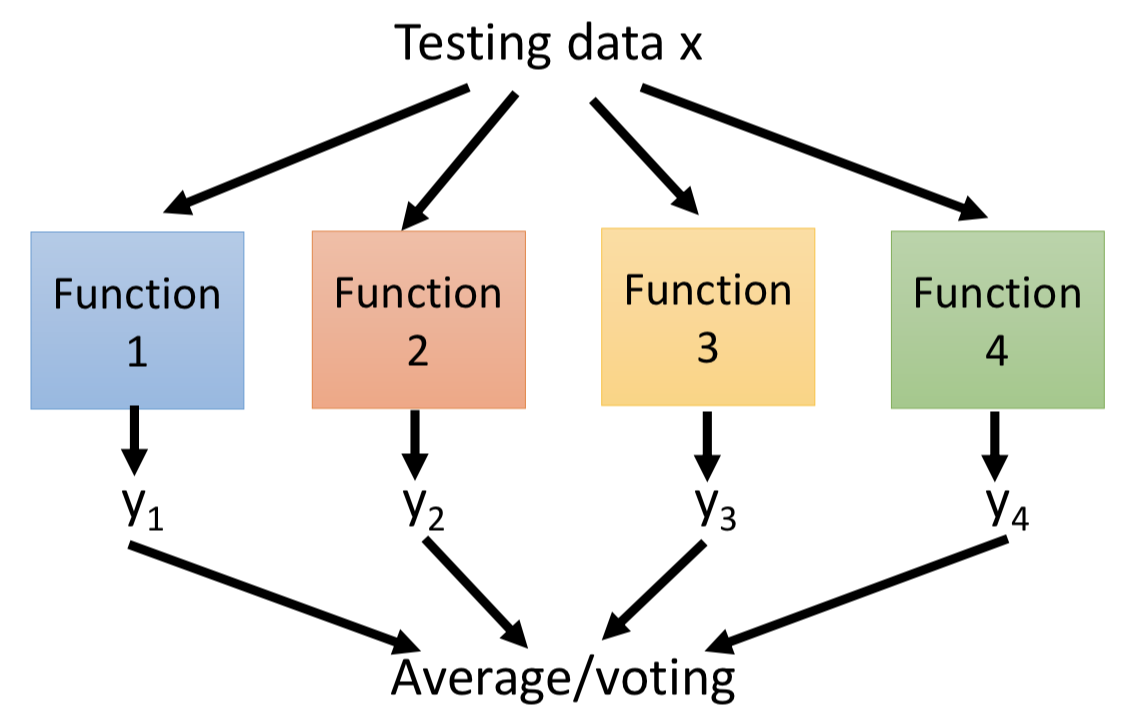
Out-of-bag validation：

用 bagging 方法不一定要把训练数据切分成训练集和验证集。因为每轮随机采样都会有一部分数据没有被采样到，可以用这部分数据来验证模型的泛化能力。

例如，训练基础模型的数据情况如下表

那就可以用 f2+f4 在 x1 上测试；f2+f3 在 x2 上测试；... ；以此类推。

Random Forest：对 decision tree 的 bagging

特点：

　1. 使用 CART 决策树作为基础模型。

　2. 只是有放回的 resample 训练数据是不够的（只这样做的话，得到每棵树都会差不多）。—— 每次分裂的时候随机限制一些特征不能用（在剩下的 p' 维特征中选择最优特征进行 split），p' 越小意味着得到的决策树模型鲁棒性越好（但同时对训练数据的拟合肯定也会变差），相当于 variance会变小但 bias 会变大，通过交叉验证选择一个合适的 p'。

　3. 对单棵树不剪枝，以此来减小单棵树的 bias（让其“专精于”那一部分特征，所以 RF 中的决策树比较深），再借助 bagging 减小整体模型的variance（相当于从不同的角度解决问题）。

推广：Isolation Forest　用于异常检测

类似 Random Forest ，不同点：

　1. 采样个数 N' 远小于训练样本个数 N。因为只需要部分样本就能够检测出异常点了。

　2. 建立决策树时，随机选择特征 + 随机选择阈值来 split 。

　3. 最大决策树深度选择一个比较小的值，原因同 1 。

对于测试样本 x，把其拟合到 T 棵决策树，计算该样本的叶子结点深度 h_t(x)，进一步计算出平均深度 h(x)。样本点是异常的概率为：

s(x, N) = 2 ^-h(x)/c(N) ; 其中 c(N) = 2log(N-1) + ξ - 2(N-1)/N ，  ξ 为欧拉常数。取值范围在[0, 1] ，越大越可能是异常点。

二、boosting

强力的保证：只要基础分类器能够在训练集上实现小于 50% 的错误率，使用 boosting 就能在训练集上实现 0% 错误率。

基础模型的训练是有顺序的（新的基础模型去补强已有的基础模型）。

怎么实现在不同的训练集上训练模型？

　1. resampling

　2. reweighting

　3. 实际应用的时候给样本不同的权重系数就行了。

Adaboost

主要思想：在让 f1(x) 的分类效果变成随机的新的训练集上训练 f2(x) ；... ；以此类推训练新的基础分类器，综合起来就是整体分类器。

怎么做？

在训练集上训练 f1(x) 得到小于 0.5 的错误率；

改变训练样本的权重参数 u ，令 f1(x) 的错误率等于 0.5 ；

在新的训练集上训练 f2(x) 得到小于 0.5 的错误率；...

具体怎么求解新的样本参数 u ？

初始化 u¹ = [1, 1, ..., 1]^T，N维向量。如果第 i 个样本 x_i 被 ft(x) 正确分类，就减小其权重参数 u_i （除以d^t）；反之，如果被分错就增大 u_i （乘d^t）。

d 的计算也很简单：

d^t = ( (1 - ε^t)/ε^t )^1/2 ，由于前提是 ft(x) 的错误率一定小于 0.5，所以 d > 1。

统一乘除两种情况的形式：令 α^t = log d^t ；乘 d^t 等价于乘 exp(α^t)，除以 d^t 等价于乘 exp(-α^t)

想办法把负号和分类情况联系起来，最后结果为：

u^t+1_i = u^t_i * exp(-yi * ft(x_i) * α^t )

得到 T 个基础分类器后，综合模型 H(x) = sign(Σ α^t * ft(x))，sum for t = 1, 2, ..., T。为什么要做 weighted sum 呢？错误率低的 ft 对应的 α^t 比较大，对最后结果影响就更大。

就完事了

证明 Adaboost 能够在训练集上实现 0% 的错误率

计算 H(x) 的错误率，发现其存在上界 exp( -y_i * g(x_i) )

等价于证明上界会越来越小。

设 Z^t 是训练 ft 的权重参数之和，可以得到 Z_T+1 的表达式，发现exp里面正好出现了g(x) = Σ α^t * ft(x)

所以，T个基础分类器构成的模型在训练集的错误率上界，就等于训练第 T+1 个基础分类器的样本权重参数的平均值。

等价于证明训练样本参数的平均值会越来越小。

根据 Z 的递推公式，发现 Z 是随 t 单调减，得证。

margin

Boosting 的一般形式：

定义优化目标为刚才求解出来的错误率上界：

怎么实现这个优化过程呢？ —— 用gradient descent

Gradient Boosting

L 对函数 g 求梯度，得到更新公式

要找到一个 ft(x) ，乘上权重 α^t 后加到 gt-1(x) 里面，和梯度下降求解得到的对 g(x) 的更新一样，那就让 ft(x) 和负梯度方向一致，也即内积越大越好。（先看方向。整体损失函数的负梯度拟合第 t 轮的损失值）

所以转换后的优化目标如下，相当于最小化 ft(x) 在权重参数为 u^t 的训练集上的误差：（ Adaboost 中的训练 ft 的步骤）

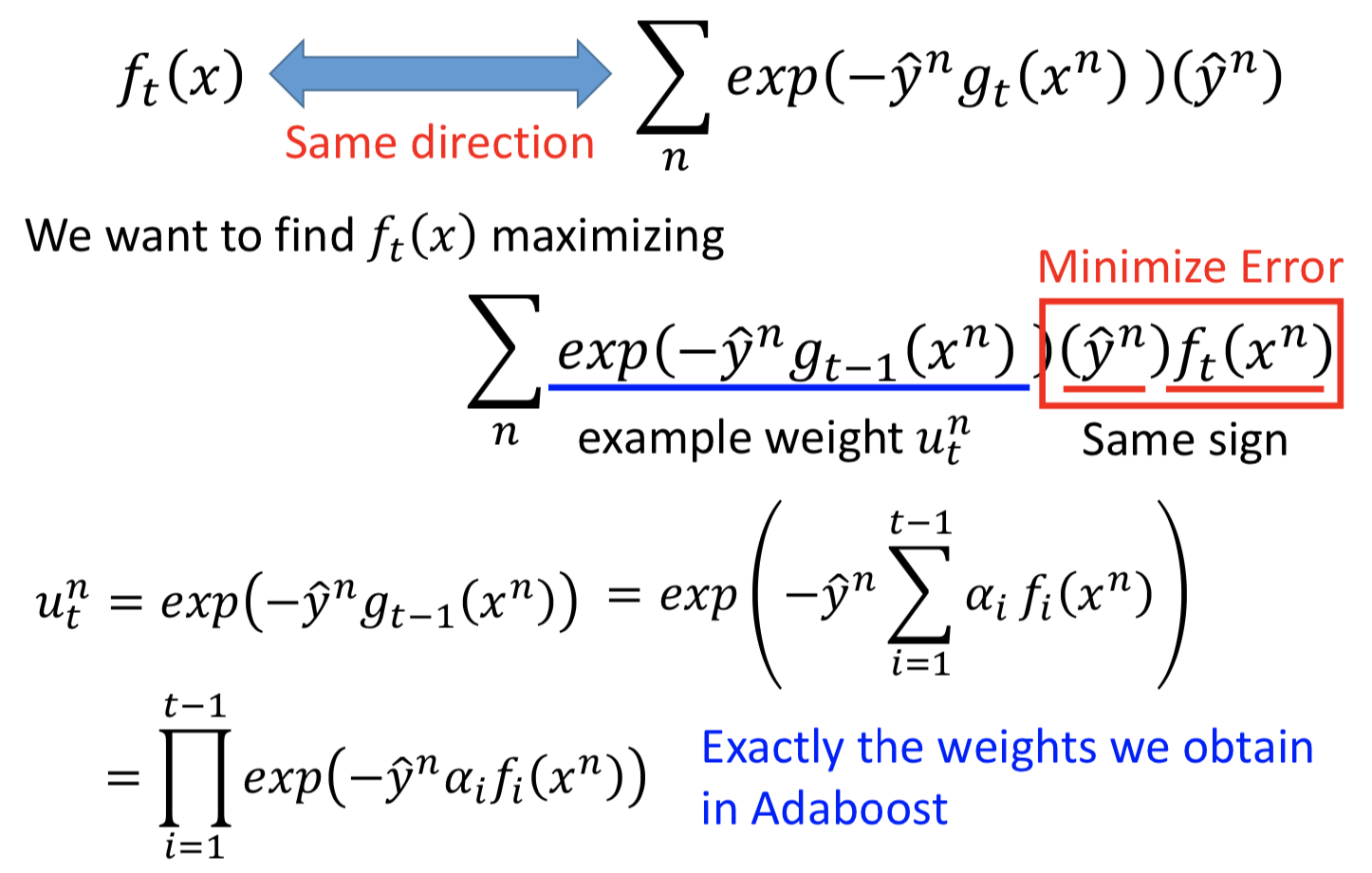
而 α^t 如何确定呢？

令 L 对 α^t 偏导数为 0 得到的解， 和Adaboost 中的定义是相同的。

三、stacking

各做各的，然后把前面已经有的模型输出作为最后一个 layer 的 new features，而且训练数据要分成两个部分，一部分用来训练前面的系统，另一部分用来训练 Final classifier。