【基本数据结构之堆】-C++

注意：这篇博客讲的是手写堆，喜欢用C++自带数据结构模拟的慎入

今天我们来聊一聊一种奇怪 的数据结构：

堆

为什么说这个数据结构有点奇怪呢？

先看看其他的在我眼里是正常的数据结构：

队列（近似于排队）

栈（类似于一个桶）

数组（就是一组存储各种数据类型的集合(?)）

但是！

堆这个东西有点奇怪，它模拟的是：

完全二叉树。

这就很让人摸不着头脑了emmmm

后来去各种找资料 知道了它的模拟方式就是：

堆的物理结构就是数组。堆的逻辑结构是一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应。如下图：



尼玛这不就是给这棵树的结点编号存数组里吗(疯狂咆哮)

接下来堆的特性我就找了一段资料如下，做了解就可以了：



感觉说的有点多…下面进入代码实现部分。今天我们以小根堆为例来进行代码实现的讲解 .

堆的基本操作：

• 上浮（up）
• 下沉（down）
• 插入（insert）
• 删除（del）
• *建立（build）

第一个是上浮（up）操作。

上浮操作，顾名思义，就是将一个结点在树中的位置尽量往上浮

代码实现用到了【位运算】不了解的可以百度一下◀〓〓

基本思路：

以小根堆为例，当小根堆的元素值h[x]变小时，该结点可能会上浮，如果h[x]小于h[x>>1]则交换两个结点的值，如此循环下去直到x=1或h[x]>=h[x>>1].

e.g.





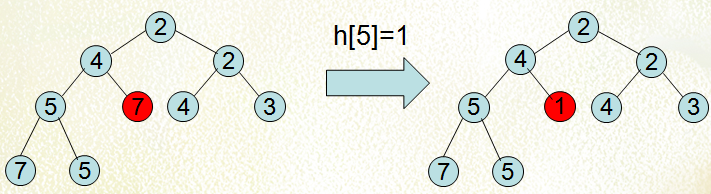
代码实现：

void up(int x)//h[x]上浮
{
   while (x>1&&h[x]<h[x>>1]){
       swap(h[x],h[x>>1]);
       x>>=1;
   }
}

时间复杂度为O(logn)。

下沉（down）操作：

思路：

当小根堆的元素值h[x]变大时，该结点可能会下沉，如果有儿子结点值小于该结点的值则跟较小儿子结点交换，如此循环下去直到条件不满足或者没有儿子结点。

代码：

void down(int x)//h[x]下沉,len是堆中元素个数
{
    int y=x<<1;
    while(y<=len){
         if(y+1<=len&&h[y+1]<h[y])y++;
         if(h[y]<h[x]){
               swap(h[x],h[y]);
               x=y;y=x<<1;
         }
         else break;
    }
}

O(logn)

插入（insert）操作：

基本思路：

插入一个元素，把该元素放在最后，再做up操作。

程序如下：

void insert(int x)
{
   h[++len]=x;
   up(len);
}

时间复杂度为O(logn)

删除(del)操作：

基本思路：

删除第x个元素，为了不破坏堆的性质，把h[len]移到x处，堆元素个数len减一，注意可能是做up(x)也可能做down(x)，根据h[x]的变化情况来定。

程序如下：

void del(int x)//删除h[x]
{
    h[x]=h[len--];
    up(x);
    down(x);
}

时间复杂度为O(logn)

*建堆(build)操作



不做过多讲述，这个操作写法有很多，也可以尝试着自己去探索其他的写法！

ov.