数据结构丨N叉树

遍历

N叉树的遍历

树的遍历

一棵二叉树可以按照前序、中序、后序或者层序来进行遍历。在这些遍历方法中，前序遍历、后序遍历和层序遍历同样可以运用到N叉树中。

回顾 - 二叉树的遍历

前序遍历 - 首先访问根节点，然后遍历左子树，最后遍历右子树；

中序遍历 - 首先遍历左子树，然后访问根节点，最后遍历右子树；

后序遍历 - 首先遍历左子树，然后遍历右子树，最后访问根节点；

层序遍历 - 按照从左到右的顺序，逐层遍历各个节点。

请注意，N叉树的中序遍历没有标准定义，中序遍历只有在二叉树中有明确的定义。尽管我们可以通过几种不同的方法来定义N叉树的中序遍历，但是这些描述都不是特别贴切，并且在实践中也不常用到，所以我们暂且跳过N叉树中序遍历的部分。

把上述关于二叉树遍历转换为N叉树遍历，我们只需把如下表述:

遍历左子树... 遍历右子树...

变为:

对于每个子节点:

通过递归地调用遍历函数来遍历以该子节点为根的子树

我们假设for循环将会按照各个节点在数据结构中的顺序进行遍历：通常按照从左到右的顺序，如下所示。

N叉树遍历示例

我们用如图所示的三叉树来举例说明:

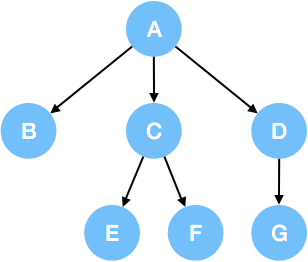
1.前序遍历

在N叉树中，前序遍历指先访问根节点，然后逐个遍历以其子节点为根的子树。

例如，上述三叉树的前序遍历是: A->B->C->E->F->D->G.

2.后序遍历

在N叉树中，后序遍历指前先逐个遍历以根节点的子节点为根的子树，最后访问根节点。

例如，上述三叉树的后序遍历是: B->E->F->C->G->D->A.

3.层序遍历

N叉树的层序遍历与二叉树的一致。通常，当我们在树中进行广度优先搜索时，我们将按层序的顺序进行遍历。

例如，上述三叉树的层序遍历是: A->B->C->D->E->F->G.

练习

接下来，我们将为你提供几道与N叉树相关的习题。

N-ary Tree Preorder Traversal

给定一个 N 叉树，返回其节点值的前序遍历。

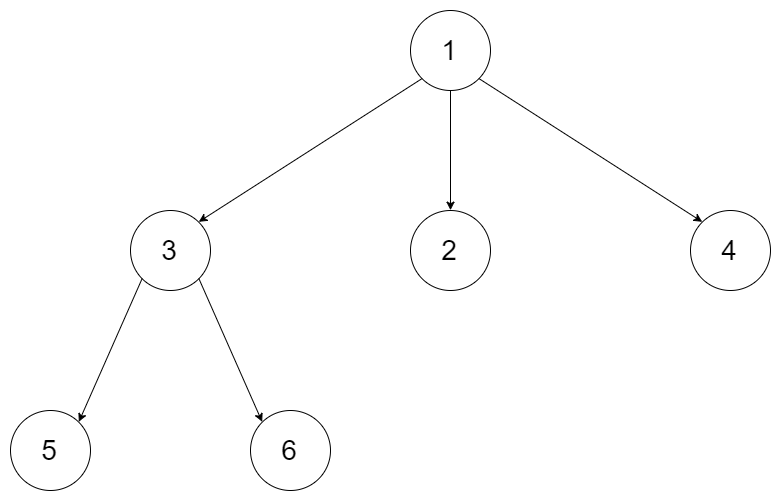
例如，给定一个 3叉树 :

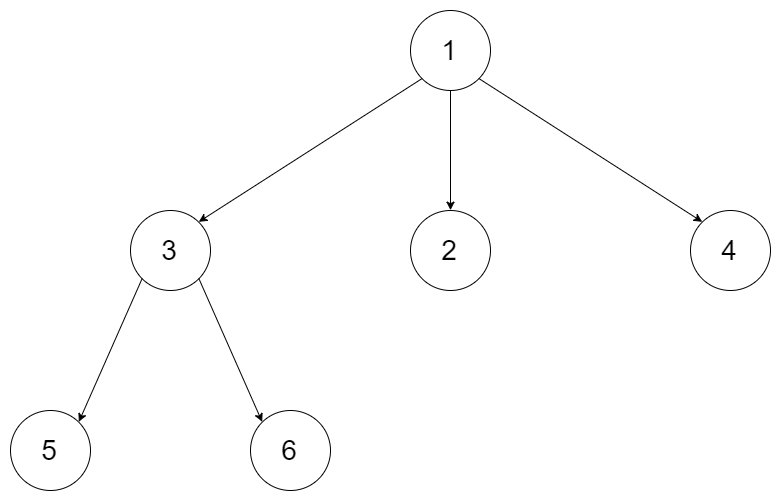
返回其前序遍历: [1,3,5,6,2,4]。

说明: 递归法很简单，你可以使用迭代法完成此题吗?

#include <iostream>
#include <vector>
#include <stack>
using namespace std;
class Node{
public:
    int val;
    vector<Node*> children;
    Node(){}
    Node(int _val, vector<Node*>_children){
        val = _val;
        children = _children;
    }
};
/// Recursion
/// Time Complexity: O(n)
/// Space Complexity: O(h)
class SolutionA{
public:
    vector<int> preorder(Node* root){
        vector<int> res;
        dfs(root, res);
        return res;
    }
private:
    void dfs(Node* node, vector<int>& res){
        if(!node)
            return;
        res.push_back(node->val);
        for(Node* next: node->children)
            dfs(next, res);
    }
};
/// Non-Recursion
/// Using stack
/// Time Complexity: O(n)
/// Space Complexity: O(h)
class SolutionB{
public:
    vector<int> preorder(Node* root){
        vector<int> res;
        if(!root)
            return res;
        stack<Node*> stack;
        stack.push(root);
        while(!stack.empty()){
            Node* cur = stack.top();
            stack.pop();
            res.push_back(cur->val);
            for(vector<Node*>::reverse_iterator iter = cur->children.rbegin();
                iter != cur->children.rend(); iter++)
                    stack.push(*iter);
        }
        return res;
    }
};
int main(){
    return 0;
}

N-ary Tree Postorder Traversal

给定一个 N 叉树，返回其节点值的后序遍历。

例如，给定一个 3叉树 :

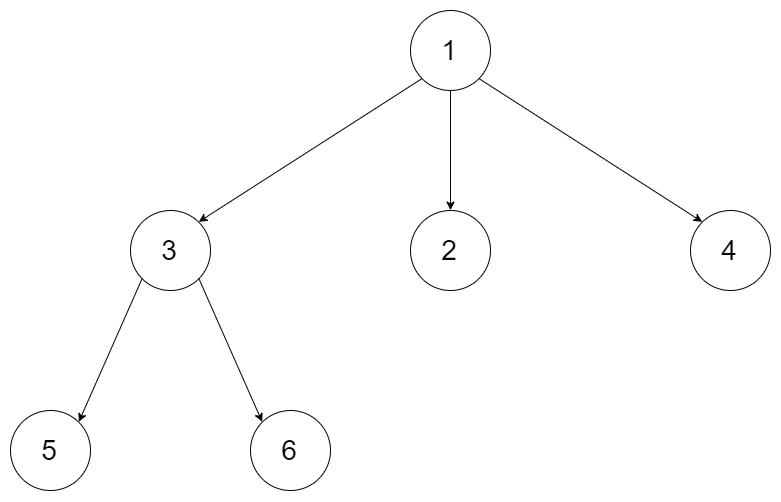
返回其后序遍历: [5,6,3,2,4,1].

说明: 递归法很简单，你可以使用迭代法完成此题吗?

#include <iostream>
#include <vector>
#include <stack>
using namespace std;
class Node{
public:
    int val;
    vector<Node*> children;
    Node(){}
    Node(int _val, vector<Node*> _children){
        val = _val;
        children = _children;
    }
};
/// Recursion
/// Time Complexity: O(n)
/// Space Complexity: O(h)
class SolutionA{
public:
    vector<int> postorder(Node* root){
        vector<int> res;
        dfs(root, res);
        return res;
    }
private:
    void dfs(Node* node, vector<int>& res){
        if(!node)
            return;
        for(Node* next: node->children)
            dfs(next, res);
        res.push_back(node->val);
    }
};
/// Non-Recursion
/// Using stack
///
/// Time Complexity: O(n)
/// Space Complexity: O(h)
class SolutionB{
public:
    vector<int> postorder(Node* root){
        vector<int> res;
        if(!root)
            return res;
        stack<Node*> stack;
        stack.push(root);
        while(!stack.empty()){
            Node* cur = stack.top();
            stack.pop();
            res.push_back(cur->val);
            for(Node* next: cur->children)
                stack.push(next);
        }
        reverse(res.begin(), res.end());
        return res;
    }
};
int main(){
    return 0;
}

N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

例如，给定一个 3叉树 :

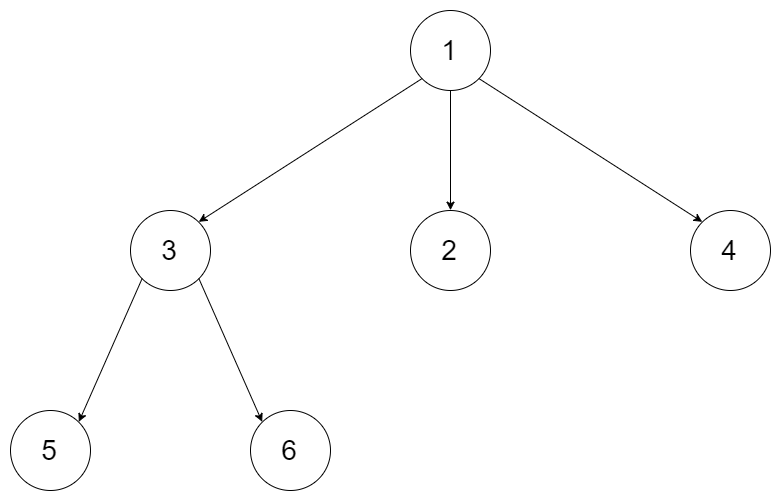
返回其层序遍历:

[
     [1],
     [3,2,4],
     [5,6]
]

说明:

树的深度不会超过 1000。
树的节点总数不会超过 5000。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class Node {
public:
    int val = NULL;
    vector<Node*> children;
    Node() {}
    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
/// BFS
/// Store step in the queue
///
/// Time Complexity: O(n)
/// Space Complexity: O(n)
class SolutionA{
public:
    vector<vector<int>> levelOrder(Node* root){
        vector<vector<int>> res;
        if(!root)
            return res;
        queue<pair<Node*, int>> q;
        q.push(make_pair(root, 0));
        while(!q.empty()){
            Node* cur = q.front().first;
            int step = q.front().second;
            q.pop();
            if(step == res.size())
                res.push_back({cur->val});
            else
                res[step].push_back(cur->val);
            for(Node* next: cur->children)
                q.push(make_pair(next, step + 1));
        }
        return res;
    }
};
int main(){
    return 0;
}

递归

N叉树的经典递归解法

经典递归法

我们在之前的章节中讲过如何运用递归法解决二叉树问题。在这篇文章中，我们着重介绍如何将这个思想引入到N叉树中。

在阅读以下内容之前，请确保你已阅读过运用递归解决树的问题这篇文章。

"自顶向下"的解决方案

"自顶向下"意味着在每个递归层次上，我们首先访问节点以获得一些值，然后在调用递归函数时，将这些值传给其子节点。

一个典型的 "自顶向下" 函数 top_down(root, params) 的工作原理如下：

1. 对于 null 节点返回一个特定值
2. 如果有需要，对当前答案 answer 进行更新                         // answer <-- params
3. for each child node root.children[k]:
4.      ans[k] = top_down(root.children[k], new_params[k])  // new_params <-- root.val, params
5. 如果有需要，返回答案 answer                                 // answer <-- all ans[k]

"自底向上"的解决方案

"自底向上" 意味着在每个递归层次上，我们首先为每个子节点递归地调用函数，然后根据返回值和根节点本身的值给出相应结果。

一个典型的 "自底向上" 函数 bottom_up(root) 的工作原理如下：

1.对于 null 节点返回一个特定值
2.for each child node root.children[k]:
3.    ans[k] = bottom_up(root.children[k]) // 为每个子节点递归地调用函数
4. 返回答案 answer                          // answer <- root.val, all ans[k]

Maximum Depth of N-ary Tree

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

例如，给定一个 3叉树 :

我们应返回其最大深度，3。

说明:

树的深度不会超过 1000。
树的节点总不会超过 5000。

#include <iostream>
#include <vector>
using namespace std;
/// DFS
/// Time Complexity: O(n)
/// Space Complexity: O(n)
/// Definition for a Node.
class Node{
public:
    int val;
    vector<Node*> children;
    Node(){}
    Node(int _val, vector<Node*> _children){
        val = _val;
        children = _children;
    }
};
class Solution{
public:
    int maxDepth(Node* root){
        if(!root)
            return 0;
        int res = 1;
        for(Node* child: root->children)
            res = max(res, 1 + maxDepth(child));
        return res;
    }
};
int main(){
    return 0;
}

小结

这张卡旨在介绍N叉树的基本思想。实际上，二叉树只是N叉树的一种特殊形式，N叉树相关问题的解决方案与二叉树的解法十分相似。因此，我们可以把在二叉树中学到的知识扩展到N叉树中。

我们提供了一些经典的N叉树习题，以便进一步帮助你理解本章中N叉树的概念。