最近公共祖先（LCA）基础模板(倍增法)

之前在澡堂学过这么个东西，听课时理解非常透彻,然后做题时是这种状态:



因为并没有切板子题,最近切掉以后看同桌,他默默地说了一句话:

我是什么时候A的来着...



我当时就心态爆炸...

现在来进行简单整理

我发现想黈之前的博客非常难,因为之前写的博客都是什么东西啊

其实我本身来讲也能理解(疯狂为下次培训不好好整理找理由)

以为澡堂给的时间其实并不多,看上去有一中午加一晚上,

但是每天学的东西都非常之多,要是把每个板子题都切下,博客中的最详细内容就只能gu掉了...

心塞...

(突然发现自己水了这么多行)

最近公共祖先在求两点最短距离时非常常用,

其定义就是两点\(u\),\(v\)的公共祖先,并且满足这个公共祖先深度尽可能大

就是这么一个东西:

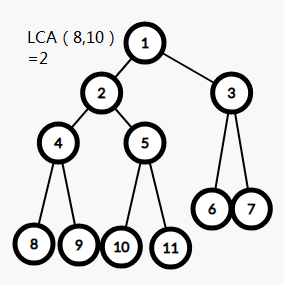
求ta的思路当然就是枚举,然而首先拿到的两个点不一定在一层,并不能直接进行暴力枚举,

那么不能将这两点调到一层以后再一个一个暴力枚举咩?

有优化算法废话还辣么多干嘛

这里介绍的方法是倍增

就是考虑往上跳\(2^n\)个祖宗,加上一定的判断,显然能够精确地跳到LCA,这样显然非常快

倍增的大体算法流程就是先将深度比较大的那个点跳到与另一个点同一深度的位置,如果此时重合,就返回其中一个点

然后一起进行倍增,直到两点的父亲为同一点,则返回其父亲



其实现思想如下(按程序步骤):

1.读入并建边建树

单纯读入并不想讲...

需要注意的是,在建边时需要建无向边,因为并不知道谁是爹

所以建无向边便于在以后进行建树操作,顺便处理出点的深度以及所有跳的爹

就是处理出这个节点的上面的第\(2^n\)个爹,(这里的\(n\)没有啥正经实际意义)

建树操作就是跑一个\(DFS\),p.s.我在某次考试用的时\(BFS\),事实证明都可以,

就建个树嘛...还能卡死哪种搜索?

\(DFS\)建树的主要思路就是拿到当前点,先处理深度,就是\(dep[爹]+1\),

这个"爹"好出戏...

然后将其"跳爹"处理出来,当然是基于之前处理过的"跳爹"

然后就是深搜主体,便利出边,将非爹节点认儿子,并进行下一步搜索,

因为建的无向边,所以儿子向着爹也有一条边,但由于爹的唯一性,这个指向爹的边有且仅有一条

同时在递归搜索时,把当前点的编号和子节点的编号一同下传,也就是说在每一次开始搜索时,都有当前节点和当前节点之爹这两个信息传下来

然后就是访问查询,(这样的题肯定不会单组询问)

写一个函数专门查询,

查询函数步骤(结合代码看下,\(f\)数组指的是跳爹):

inline int lca(int l,int r){
	if(dep[l]<dep[r]) swap(l,r);
	for(int i=20;i>=0;i--){
		if(dep[f[l][i]]>=dep[r])l=f[l][i];
		if(l==r) return l;
	}
	for(int i=20;i>=0;i--){
		if(f[l][i]!=f[r][i]){
			l=f[l][i];
			r=f[r][i];
		}
	}return f[l][0];
}

1.使方便处理的节点深度大,就是函数内第一行的意义,这样好处理

2.使两节点跳到同一层,当然要让\(i\)从大到小枚举,这样满足倍增的思想

好像这是正文里第一次出现倍增这个词...

就是先跳大步,跳不了跳小步,通过预处理各种条件(比如深度和\(2^n\)个祖宗)来提供判断所需依据

当然如果当两节点在同一层时也在同一点,那么他们所在位置已经是LCA了,这种情况的出现当且仅当访问数据中出现存在父子(或祖孙啥的)关系

那么下面就是倍增主环节

同样\(i\)要从大到小枚举,道理相同

然而这里的判断条件是"祖宗不同就跳"

毕竟不能跳过嘛,比如在这棵树中:

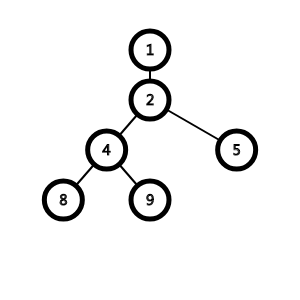
显然\(f[8][1]==f[9][1]==2\),然而ta们的LCA并不是2,

所以就是跳过了

所以判断的条件就是爹不统一,

按照这个法则跳可以始终保证目前节点在LCA下面

这样跳到的最终结果就是其LCA的儿子

此时返回\(f[l][0]\)就行辣_{\(≧▽≦)/}

完整代码奉上:

#include<bits/stdc++.h>
using namespace std;
int n,m,s;
struct Ed{
	int to,nxt;
}ed[1000005];
int head[1000005];
int dep[1000005];
int f[1000005][21];
int ednum;
inline void add(const int &from,const int &to){
	ed[++ednum].nxt=head[from];
	ed[ednum].to=to;
	head[from]=ednum;
}
inline void search(const int &u,const int &fa){
	dep[u]=dep[fa]+1;
	for(int i=1;(1<<i)<=dep[u];i++)
		f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];i;i=ed[i].nxt){
		int v=ed[i].to;
		if(v==fa) continue;
		f[v][0]=u;
		search(v,u);
	}
}
inline int lca(int l,int r){
	if(dep[l]<dep[r]) swap(l,r);
	for(int i=20;i>=0;i--){
		if(dep[f[l][i]]>=dep[r])l=f[l][i];
		if(l==r) return l;
	}
	for(int i=20;i>=0;i--){
		if(f[l][i]!=f[r][i]){
			l=f[l][i];
			r=f[r][i];
		}
	}return f[l][0];
}
int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<n;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
		add(b,a);
	}
	search(s,0);
	while(m--){
		int a,b;
		scanf("%d%d",&a,&b);
		printf("%d\n",lca(a,b));
	}return 0;
}

突然想起还有单调队列板子要整,

可是要放假了啊

窗外...白鸽飞过...