CS184.1X 计算机图形学导论 罗德里格斯公式推导

罗德里格斯公式推导

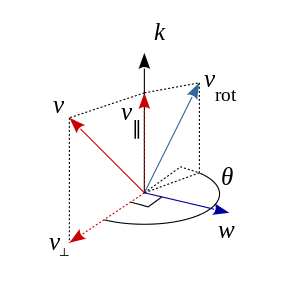
图1（复制自wiki)

按照教程里，以图1为例子,设k为旋转轴，v为原始向量。 v以k为旋转轴旋转，旋转角度为θ，旋转后的向量为v_rot。

首先我们对v进行分解，分解成一个平行于k和垂直于K的向量，分别为v_∥和v_⊥。

则v_∥=<k,v>k (因为这里设了k是单位向量，所以|k|=1)

v_⊥=v-v_∥

为了方便研究旋转后的向量，我们以k和v的叉乘w以及v_∥和v_⊥建立坐标系。
w=kXv

设v_rot的分量为v_⊥',和v_∥',显而易见的v_∥'=v_∥
而v_⊥'可以由v_⊥和w来表示。
由于v_⊥'是v_rot的分量，因此显而易见的|v_⊥'|=|v_⊥|
设k和v之间的夹角为α
w=kXv，即|w|=|k||v|sinα
从图中我们根据三角形公式，也可以得出|v_⊥|=|v|sinα,而|k|=1，所以|v_⊥|=|w|

因此，v_⊥'=wsinθ+v_⊥cosθ
v_rot=wsinθ+v_⊥cosθ+v_∥

w=kXv
v_∥=<k,v>k

v_⊥=v-v_∥
<k,v>k=k^Tvk（根据点乘转换成矩阵）= kk^Tv(可验证)
kXv=K^*v （设K^*为k的对偶矩阵）（根据叉乘转矩阵的方法）

v_rot=K^*vsinθ+(v- kk^Tv)cosθ+kk^Tv
=(K^*sinθ+Icosθ+kk^T(1-cosθ))v

最后得出旋转公式R=K^*sinθ+Icosθ+kk^T(1-cosθ)