NOIP模拟测试2-5
该补一下以前挖的坑了
先总结一下
第二次
T1 搜索+剪枝
#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;
const int maxn=;
int a[maxn],n,js[maxn];
bool jk[maxn];
ll ans;
bool judge(int l,int r)
{
int i=l;
while(i<r)
{
if(a[i]+!=a[i+])return ;
else i++;
}
return ;
}
void out()
{
for(int i=;i<=(<<n);i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
void search(int num,int last)
{
//out();//cout<<"->"<<endl;
if(judge(,<<n)){ans+=js[num];return ;}
if(last==n+)return ;
int must1=,must2=;
for(int j=;j<=(<<n);j+=(<<last))
{
if(!judge(j,j+(<<last)-)&&!must1)must1=j;
else if(!judge(j,j+(<<last)-)&&must1&&!must2)must2=j;
else if(!judge(j,j+(<<last)-))return ;
}
if(!must1&&!must2)search(num,last+);
else if(!must2)
{
int j=must1,k=must1+(<<(last-));
int kx=;
while(kx<(<<(last-)))
{
swap(a[j+kx],a[k+kx]);
kx++;
}
search(num+,last+);
kx=;
while(kx<(<<(last-)))
{
swap(a[j+kx],a[k+kx]);
kx++;
}
return ;
}
else
{
int jj[]={},kk[]={};
// cout<<must1<<" "<<must2<<endl;
jj[]=must1,jj[]=must1+(<<(last-));
kk[]=must2,kk[]=must2+(<<(last-));
//cout<<jj[1]<<" "<<kk[1]<<endl;
for(int i=;i<=;i++)
for(int j=;j<=;j++)
{
//out();
//cout<<jj[i]<<" "<<kk[j]<<endl;
int kx=;
while(kx<(<<(last-)))
{
swap(a[jj[i]+kx],a[kk[j]+kx]);
kx++;
}
search(num+,last+);
kx=;
while(kx<(<<(last-)))
{
swap(a[jj[i]+kx],a[kk[j]+kx]);
kx++;
} }
}
return ;
}
int main()
{
scanf("%d",&n);
js[]=;
for(int i=;i<=n;i++)
js[i]=js[i-]*i;
for(int i=;i<=(<<n);i++)
{
scanf("%d",&a[i]);
}
search(,);
cout<<ans<<endl;
return ;
}
T2 划艇 高难标记
31分算法：线段树优化DP
AC算法：
区间离散化。
跨区间显然，同区间组合计数。
#include<cstdio>
#include<iostream>
#include<algorithm>
#define mod DeepinC
#define maxn 505
using namespace std;
int l[maxn*],len[maxn*],sum[maxn*][maxn*],num[maxn*][maxn*],a[maxn],b[maxn],f[maxn][maxn*],inv[maxn*+];
const int mod=1e9+;
int qpower(int a,int b)
{
int ans=;
while(b)
{
if(b&)ans=1ll*ans*a%mod;
b>>=;
a=1ll*a*a%mod;
}
return ans;
}
void get_inv()
{
for(int i=;i<=;i++)
inv[i]=qpower(i,mod-);
return ;
}
int main()
{
get_inv();
int n,tot=,ans=;
scanf("%d",&n);
for(int i=;i<=n;i++)
{
scanf("%d%d",&a[i],&b[i]);
b[i]++;
l[++tot]=a[i];
l[++tot]=b[i];
}
sort(l+,l+tot+);
tot=unique(l+,l+tot+)-l-;
for(int i=;i<tot;i++)
{
len[i]=l[i+]-l[i];
//cout<<i<<" "<<len[i]<<endl;
}
for(int i=;i<=n;i++)
{
a[i]=lower_bound(l+,l+tot+,a[i])-l;
b[i]=lower_bound(l+,l+tot+,b[i])-l-;
}
sum[][]=;
for(int i=;i<=n;i++)
{
sum[i][]=;
}
for(int j=;j<=tot;j++)sum[][j]=;
for(int i=;i<=n;i++)
{
for(int j=a[i];j<=b[i];j++)
{
f[i][j]=1ll*sum[i-][j-]*len[j]%mod;
// cout<<f[i][j]<<endl;
int o=,C=(len[j]-)%mod;
for(int k=i-;k;k--)
{
if(a[k]>j||b[k]<j)continue;
o++;
C=1ll*C*(o+len[j]-)%mod*inv[o]%mod;
//cout<<C<<endl;
f[i][j]=(f[i][j]+1ll*C*sum[k-][j-]%mod)%mod;
}
///cout<<f[i][j]<<endl;
ans+=f[i][j];
ans%=mod;
}
for(int j=;j<=tot;j++)
sum[i][j]=((1ll*sum[i-][j]+sum[i][j-])%mod-sum[i-][j-]+f[i][j]+mod)%mod;
}
cout<<ans<<endl;
return ;
}
T3 放棋子：DP
设g[i][j][k]表示用k个棋子填满i行j列的方案，设f[i][j][k]表示用前k种棋子填满i行j列的方案
容斥计算g数组：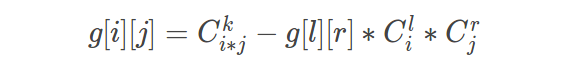
那么f数组 ：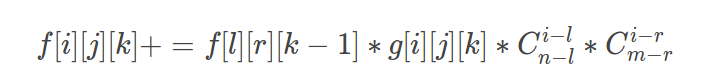
最终答案：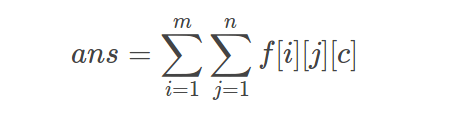
（图片来自https://www.cnblogs.com/yanshannan/p/9467292.html，特此鸣谢）
AC代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#define maxn 35
using namespace std;
const int mod=1e9+;
int C[maxn*maxn][maxn*maxn],g[maxn][maxn],f[maxn][maxn][maxn*maxn],cn[maxn];
int moded(int x)
{
if(x<)return x+mod;
return x>=mod?x-mod:x;
}
int main()
{
// freopen("out.txt","w",stdout);
int n,m,c,tot=;
scanf("%d%d%d",&n,&m,&c);
for(int i=;i<=c;i++)
{
scanf("%d",&cn[i]);
tot=max(tot,cn[i]);
}
for(int i=;i<=;i++)
{
C[i][]=C[i][i]=;
for(int j=;j<i;j++)
C[i][j]=(C[i-][j]+C[i-][j-])%mod;
}
f[][][]=;
int ans=;
for(int k=;k<=c;k++)
{
memset(g,,sizeof(g));
for(int i=;i<=n;i++)
for(int j=;j<=m;j++)
{
g[i][j]=C[i*j][cn[k]];
for(int ii=;ii<=i;ii++)
for(int jj=;jj<=j;jj++)
{
if(ii==i&&jj==j)continue;
g[i][j]=(g[i][j]-1ll*g[ii][jj]*C[i][ii]%mod*C[j][jj]%mod+mod)%mod;
}
//cout<<k<<" "<<i<<" "<<j<<" "<<" "<<g[i][j]<<endl;
}
for(int i=;i<=n;i++)
for(int j=;j<=m;j++)
{
for(int ii=;ii<i;ii++)
for(int jj=;jj<j;jj++)
{
f[i][j][k]=(f[i][j][k]+1ll*f[ii][jj][k-]*C[n-ii][i-ii]%mod*C[m-jj][j-jj]%mod*g[i-ii][j-jj]%mod)%mod;
//if(k==c&&i==n&&j==m)cout<<ii<<" "<<jj<<" "<<f[ii][jj][k-1]<<endl;
}
if(k==c)
{
ans=moded(ans+f[i][j][c]);
//if(i==n)cout<<i<<" "<<j<<" "<<f[i][j][c]<<endl;
}
} }
cout<<ans<<endl;
return ;
}
第三次
爆零。。。
T1：序列
乱搞，（鬼知道我打了一个什么倍增）
AC代码：（不会告诉你我是QJ的）
感谢wd大佬的帮助%%DeepinC
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#define maxn 200005
#define maxq 1001
#include<vector>
#include<algorithm>
#define LL long long
#define ts puts("--------");
using namespace std;
LL n,a[maxn],ans,need1[maxn],A[maxn],maxx,b[maxn][],num[maxn],fr[maxn][],Num[],nuM[],toty;
LL prime[maxq*+],tot,frprime[maxq*+];
bool isnotprime[maxq*+];
LL gcd(LL a,LL b)
{
return b==?a:gcd(b,a%b);
}
LL qpower(LL a,LL b)
{
LL ans=;
while(b)
{
if(b&)ans=ans*a;
a=a*a;
b>>=;
}
return ans;
}
void pre()
{
for(int i=;i<=maxq*;i++)
{
if(!isnotprime[i])
{
prime[++toty]=i;
frprime[i]=i;
}
for(int j=;j<=toty;j++)
{
if(i*prime[j]>maxq*)break;
isnotprime[i*prime[j]]=;
frprime[i*prime[j]]=prime[j];
if(!i%prime[j])break;
}
}
}
LL GetUse(LL x)
{
LL mt=x;
if(x%==){
while(x%==)x/=;
return x==?10ll:mt;
}
if(x%==){
while(x%==)x/=;
return x==?7ll:mt;
}
if(x%==){
while(x%==)x/=;
return x==?6ll:mt;
}
if(x%==){
while(x%==)x/=;
return x==?5ll:mt;
}
if(x%==){
while(x%==)x/=;
return x==?:mt;
}
if(x%==){
while(x%==)x/=;
return x==?:mt;
}
return mt;
}
bool query(LL st,LL len)
{
LL cnt=;
for(LL i=st;i<=st+len-;i++)
{
num[++cnt]=a[i];
}
sort(num+,num+cnt+);
for(LL i=;i<=cnt;i++)if(num[i]==num[i-]){return ;}
return ;
}
LL Get(LL x,LL q)
{
if(q==)return x;
while(x%q==)x/=q;
return x;
}
bool judge(LL len)
{
LL Q=,now,F;
for(LL i=;i<=n-len+;i++)
{
now=;Q=;
for(LL t=;t>=;t--)
{
if((<<t)+now<=len){
if(b[i+now][t]==-){break;}
// cout<<i<<' '<<len<<' '<<t<<' '<<now<<" from "<<n-len+1<<endl;
if(!Q){Q=b[i+now][t];F=fr[i+now][t];}
else if(b[i+now][t]==-||Q!=b[i+now][t]||fr[i+now][t]!=F){break;}
now+=(<<t);
if(now==len){
if(Q==||query(i,len))return ;
else break;
}
if(now==len-){
if(Q==&&a[i+len-]==a[i+len-])return ;
if(a[i+len-]>a[i+len-]&&query(i,len)&&a[i+len-]%a[i+len-]==)
{
LL t=a[i+len-]/a[i+len-];
if(GetUse(t)==Q)return ;
}
else
if(a[i+len-]<a[i+len-]&&query(i,len)&&a[i+len-]%a[i+len-]==)
{
LL t=a[i+len-]/a[i+len-];
if(GetUse(t)==Q)return ;
}
break;
}
}
}
}
return ;
}
int main()
{
scanf("%lld",&n);
for(LL i=;i<=n;i++)scanf("%lld",&a[i]);
for(LL i=;i<=n;i++)
if(a[i]%a[i-]==){
b[i-][]=a[i]/a[i-];
b[i-][]=GetUse(b[i-][]);
fr[i-][]=Get(a[i-],b[i-][]);
}
else if(a[i-]%a[i]==){
b[i-][]=a[i-]/a[i];
b[i-][]=GetUse(b[i-][]);
fr[i-][]=Get(a[i],b[i-][]);
}
else b[i-][]=-;
b[n][]=-;
for(LL i=;i<=;i++)
for(LL j=;j<=n;j++){
if(b[j][i-]==b[j+(<<(i-))][i-]&&b[j][i-]!=-&&fr[j][i-]==fr[j+(<<(i-))][i-])
b[j][i]=b[j][i-],fr[j][i]=fr[j][i-];
else b[j][i]=-;
}
LL l=,r=n;
while(l<=r)
{
int mid=l+r>>;
if(judge(mid)){ans=mid;l=mid+;}
else r=mid-;
}
cout<<ans<<endl;
return ;
}
T2：熟练剖分
概率期望不是DP
值得一提的是,wq学长为我们证明了某种树DP复杂度（枚举深度，子树大小。。）：设（x,y）表示树上的一对节点对，那么考虑每个节点的贡献，每个节点会被它的父链上的每个节点计算一次，所以每个节点被计算n次即总复杂度n×n。
还有很重要的是，打成相加形式才是n^2,不然是n^3
n^2
1 for(int j=size[x];j>=0;j--)
2 {
3 for(int k=0;k<=min(j,size[y]);k++)
4 {
5 f[x][j][1]=min(f[x][j][1],f[x][j-k][1]+f[y][k][1]);
6 f[x][j][0]=min(f[x][j][0],f[x][j-k][0]+min(f[y][k][0],f[y][k][1]));
7 }
8 }
n^3
1 for(int j=size[x];j>=0;j--)
2 {
3 for(int k=size[y];k>=0;k--)
4 {
5 f[x][j+k][1]=min(f[x][j+k][1],f[x][j][1]+f[y][k][1]);
6 f[x][j+k][0]=min(f[x][j+k][0],f[x][j][0]+min(f[y][k][0],f[y][k][1]));
7 }
8 }
这道题就是这一类
AC代码：
#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
const int mod=1e9+;
int n,indu[],root;
vector<int>son[];
long long f[][],g[][][],dep[];
long long pow(long long a,long long b){
long long ans=;
a%=mod;
while(b){
if(b&) ans=(ans*a)%mod;
b>>=;
a=(a*a)%mod;
}
return ans%mod;
}
long long max(long long a,long long b){
return a>b?a:b;
}
void dfs(int x){
if(son[x].size()==){
f[x][]=;
//printf("x=%d 代价=%d 方案数=%d\n",x,0,f[x][0]);
return;
}
for(int i=;i<son[x].size();i++){
dfs(son[x][i]);
dep[x]=max(dep[x],dep[son[x][i]]+);
}
memset(g,,sizeof(g));
for(int i=;i<=dep[son[x][]]+;i++){
g[][][i]=f[son[x][]][i-];
g[][][i]=f[son[x][]][i];
//printf("g[%d][%d][%d]=%d g[%d][%d][%d]=%d\n",0,0,i,g[0][0][i],0,1,i,g[0][1][i]);
}
g[][][]=f[son[x][]][];
int cur=,upw=dep[son[x][]]+;
for(int i=;i<son[x].size();i++){
memset(g[cur^],,sizeof(g[cur^]));
for(int j=;j<=upw;j++){
for(int k=;k<=dep[son[x][i]];k++){
(g[cur^][][max(j,k+)]+=g[cur][][j]*f[son[x][i]][k]%mod)%=mod;
(g[cur^][][max(j,k+)]+=g[cur][][j]*f[son[x][i]][k]%mod)%=mod;
(g[cur^][][max(j,k)]+=g[cur][][j]*f[son[x][i]][k]%mod)%=mod;
}
}
upw=max(dep[son[x][i]]+,upw);
cur^=;
}
memcpy(f[x],g[cur][],sizeof(f[x]));
//for(int i=0;i<=dep[x];i++) printf("x=%d 代价=%d 方案=%d\n",x,i,f[x][i]); }
int main(){
scanf("%d",&n);
int x,y;
long long num=;
for(int i=;i<=n;i++){
scanf("%d",&x);
for(int j=;j<=x;j++){
scanf("%d",&y);
son[i].push_back(y);
indu[y]++;
}
if(x) (num*=pow(x,mod-)%mod)%=mod;
}
for(int i=;i<=n;i++){
if(indu[i]==){
root=i;
break;
}
}
dfs(root);
long long sum=;
for(int i=;i<=n;i++) sum=(sum+i*f[root][i]%mod)%mod;
//cout<<sum<<" "<<num<<endl;
printf("%lld\n",(sum%mod*num%mod)%mod);
}
T3：建造游乐场 高难标记
毒瘤题，码量极短，思维量极高23333333
为了保证考试总结的完整性 我决定借用外力（粘贴题解）
先不粘AC代码了（心虚）
第四次
T1 礼物：
实际上是个及其简单的概率期望
But....我经过一下午的钻研（死皮赖脸缠着学长）（以致学长无法吃鸡）才大致明白了
f[i]=∑f[s]*p[j]+∑p[j]*f[i]+1
因为设f[i]表示买到状态为i到最终状态的期望次数
那么那么f[i]是可以由他的下一个状态转移过来
即所有的f[s].如果按原有的逻辑顺序对于f[i]来说转移到f[s]的概率是显然的
但是因为是倒着推，很显然f[s]就应该累加到f[i]上所以：
正向求概率，反向求期望！
#include<cstdio>
#include<iostream>
#define MAXN 25
using namespace std;
double p[MAXN],f[<<],wp[MAXN];
int w[MAXN];
int main()
{
int n;long long ans1=;
scanf("%d",&n);
int maxk=(<<n)-;
for(int i=;i<=n;i++)
{
scanf("%lf%d",&p[i],&w[i]);
ans1+=w[i];
}
cout<<ans1<<endl;
f[maxk]=;
for(int i=;i<=maxk;i++)
{
int state=i;
for(int j=;j<=n;j++)
{
if((state&(<<(j-))))continue;
wp[state]+=p[j];
}
}
for(int i=maxk-;i>=;i--)
{
f[i]=;
for(int j=;j<=n;j++)
{
if((i&(<<(j-))))continue;
f[i]+=(f[i|(<<(j-))]*p[j]);
}
f[i]/=wp[i];
//cout<<i<<' '<<f[i]<<endl;
}
printf("%.3lf",f[]);
return ;
}
T2：通讯
Tarjan缩点+贪心板子题
#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
#define LL long long
#define mem(a) memset(a,0,sizeof(a))
#define MAXN 200005
#define LL long long
using namespace std;
struct node{
LL to[MAXN],head[MAXN],w[MAXN],nxt[MAXN],d[MAXN],low[MAXN],dfn[MAXN],s[MAXN],top,tot,num,out[MAXN],n,m,c[MAXN];
LL To[MAXN],Head[MAXN],W[MAXN],Nxt[MAXN],cnt,Cnt,ans;
bool in_s[MAXN];
void clear()
{
mem(head);mem(Head);cnt=Cnt=ans=tot=top=num=;mem(in_s);mem(dfn);
}
void add(LL u,LL v,LL val)
{
to[++cnt]=v;
nxt[cnt]=head[u];
w[cnt]=val;
head[u]=cnt;
return ;
}
void Add(LL u,LL v,LL val)
{
To[++Cnt]=v;
Nxt[Cnt]=Head[u];
W[Cnt]=val;
Head[u]=Cnt;
return ;
}
void Tarjan(LL x)
{
dfn[x]=low[x]=++tot;
s[++top]=x;
in_s[x]=;
for(LL i=head[x];i;i=nxt[i])
{
LL y=to[i];
if(!dfn[y])
{
Tarjan(y);
low[x]=min(low[x],low[y]);
}
else if(in_s[y])
{
low[x]=min(low[x],dfn[y]);
}
}
if(low[x]==dfn[x])
{
num++;
while(top)
{
LL p=s[top--];
in_s[p]=;
c[p]=num;
if(p==x)break;
}
}
}
void toposort()
{
queue<int>Q;
memset(d,0x3f,sizeof(d));
d[c[]]=;
Q.push(c[]);
while(!Q.empty())
{
LL x=Q.front();Q.pop();
for(LL i=Head[x];i;i=Nxt[i])
{
LL y=To[i];
out[y]--;
if(W[i]<d[y])
{
d[y]=W[i];
}
if(!out[y])Q.push(y);
}
}
return ;
}
void Build_new()
{
for(LL i=;i<=n;i++)
for(LL j=head[i];j;j=nxt[j])
{
LL k=to[j];
if(c[i]!=c[k])
{
Add(c[i],c[k],w[j]);
out[c[k]]++;
}
}
}
inline LL Rd()
{
register LL x=;char c=getchar();
while(c>''||c<'')c=getchar();
while(c<=''&&c>=''){x=x*+c-'';c=getchar();}
return x;
}
void work()
{
while()
{
n=Rd(),m=Rd();
if(n==&&m==)return ;
clear();
while(m--)
{
LL a=Rd(),b=Rd(),c=Rd();
a++;b++;
add(a,b,c);
}
Tarjan();
Build_new();
toposort();
for(LL i=;i<=num;i++)ans+=d[i];
cout<<ans<<endl;
}
}
}E;
int main()
{
E.work();
return ;
}
T3：奇袭（我不会玩甘宁啊） 高难标记
27分算法：维护前缀和扫描
74分算法：维护最大最小值
AC算法：分治
再次膜拜DeepinC
AC代码：
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 50005
using namespace std;
int ans;
int w[MAXN],mi[MAXN],ma[MAXN],t[MAXN*],n;
inline int Rd()
{
int x=;char c=getchar();
while(c<''||c>'')c=getchar();
while(c>=''&&c<=''){x=x*+c-;c=getchar();}
return x;
}
int solve(int l,int r)
{
if(l==r)return ;
int mid=l+r>>;
int lans=solve(l,mid),rans=solve(mid+,r);
ans=lans+rans;
ma[mid]=mi[mid]=w[mid];
ma[mid+]=mi[mid+]=w[mid+];
for(int i=mid-;i>=l;i--)
{
ma[i]=max(w[i],ma[i+]);
mi[i]=min(w[i],mi[i+]);
}
for(int i=mid+;i<=r;i++)
{
ma[i]=max(ma[i-],w[i]);
mi[i]=min(mi[i-],w[i]);
}
for(int i=mid;i>=l;i--)
{
int j=ma[i]-mi[i]+i;
if(j>mid&&j<=r&&ma[j]<=ma[i]&&mi[j]>=mi[i])ans++;
}
for(int i=mid+;i<=r;i++)
{
int j=i-ma[i]+mi[i];
if(j<=mid&&j>=l&&ma[j]<=ma[i]&&mi[j]>=mi[i])ans++;
}
int head,tail;
head=tail=mid+;
for(int i=mid;i>=l;i--)// maxn in left && minn in right mi[j]<mi[i] && ma[j] <ma[i]
{
while(ma[tail]<=ma[i]&&tail<=r){t[tail+mi[tail]]++;tail++;}
while(mi[head]>=mi[i]&&head<=r){t[head+mi[head]]--;head++;}
if(t[i+ma[i]]>)ans+=t[i+ma[i]];
}
while(head<tail){t[head+mi[head]]--;head++;}
while(tail<head){t[tail+mi[tail]]++;tail++;}
head=tail=mid;
for(int i=mid+;i<=r;i++)
{
while(ma[tail]<=ma[i]&&tail>=l){t[tail-mi[tail]+MAXN]++;tail--;}
while(mi[head]>=mi[i]&&head>=l){t[head-mi[head]+MAXN]--;head--;}
if(t[MAXN+i-ma[i]]>)ans+=t[MAXN+i-ma[i]];
}
while(head>tail){t[head-mi[head]+MAXN]--;head--;}
while(tail>head){t[tail-mi[tail]+MAXN]++;tail--;}
return ans;
}
int main()
{
// freopen("da.in","r",stdin);
// freopen("my.out","w",stdout);
n=Rd();
for(int i=;i<=n;i++)
{
int a=Rd(),b=Rd();
w[a]=b;
}
printf("%d\n",solve(,n));
return ;
}
/*
8
1 2
2 6
3 1
4 7
5 3
6 5
7 4
8 8
*/
第五次
T1：星际旅行
考试想到正解，没有判连通
AC代码：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const long long MAXN=;
long long n,m,out[MAXN],s[MAXN],t[MAXN],add,addy;
long long C[MAXN][];
long long ans;
int f[MAXN],siz[MAXN];
bool vst[MAXN];
inline long long Rd()
{
register long long x=;
char c=getchar();
while(c>''||c<'')c=getchar();
while(c>=''&&c<=''){x=x*+c-;c=getchar();}
return x;
}
int Get(int a)
{
return f[a]==a?a:f[a]=Get(f[a]);
}
void un_ion(int a,int b)
{
int fa=Get(a),fb=Get(b);
f[fa]=fb;
siz[fb]+=siz[fa];
}
int main()
{
// freopen("out.in","r",stdin);
// freopen("a.txt","w",stdout);
n=Rd();m=Rd();
for(int i=;i<=n;i++)f[i]=i,siz[i]=;
for(long long i=;i<=m;i++)
{
s[i]=Rd();t[i]=Rd();
vst[s[i]]=vst[t[i]]=;
if(Get(s[i])!=Get(t[i]))un_ion(s[i],t[i]);
if(s[i]==t[i]){add++;ans+=m-add;}
else {out[s[i]]++;out[t[i]]++;addy++;}
}
int xup=;
for(int i=;i<=n;i++)if(!vst[i])xup++;
for(int i=;i<=n;i++)
if(vst[i]&&siz[Get(i)]!=n-xup){cout<<<<endl;return ;}
else if(vst[i]) break;
C[][]=C[][]=;
for(long long i=;i<=m;i++)
{
C[i][]=;
for(long long j=;j<=;j++)
C[i][j]=C[i-][j-]+C[i-][j];
}
for(long long i=;i<=n;i++)
ans+=C[out[i]][];
cout<<ans<<endl;
return ;
}
T2：砍树
数论分块。
显然：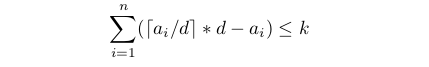
辣么移项后易得：（本博猪没有图，自行脑补)。
#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
int n;
long long m,a[],maxn;
vector<long long>ok;
int judge(long long x){
long long len=;
for(int i=;i<=n;i++){
int g=ceil((double)a[i]/(double)x);
len+=(long long)g;
}
//cout<<x<<" "<<len<<endl;
if(x<=m/len) return ;
return ;
}
int main(){
scanf("%d%lld",&n,&m);
for(int i=;i<=n;i++) scanf("%lld",&a[i]),m+=a[i],maxn=max(a[i],maxn);
// cout<<"fsdf"<<endl;
//maxn=1000000;
for(long long i=;i<=m;i++){
long long sg=;
for(int j=;j<=n;j++){
sg+=ceil((double)a[j]/(double)i);
}
//cout<<i<<" "<<sg<<endl;
long long sb=m/sg;
//cout<<sb<<endl;
ok.push_back(sb);
i=m/(m/i);
}
long long ans=;
sort(ok.begin(),ok.end());
for(int i=ok.size()-;i>=;i--){
// cout<<ok[i]<<endl;
if(judge(ok[i])){
ans=ok[i];
break;
}
}
printf("%lld\n",ans);
}
T3：超级树
再次借用wd大佬题解
AC代码：
#include<cstdio>
#include<iostream>
#define LL long long
#define MAXN 305
using namespace std;
LL dp[MAXN][MAXN],siz[MAXN];
int main()
{
LL k,mod;
scanf("%lld%lld",&k,&mod);
dp[][]=dp[][]=;
siz[]=;
for(int i=;i<=k;i++)
{
if(siz[i-]<k)siz[i]=siz[i-]+siz[i-]+;
else siz[i]=k+;
for(int l=;l<=min(k,siz[i-]);l++)
for(int r=;r<=min(k,siz[i-]);r++)
{
if(l+r>k)break;
LL num=dp[i-][l]*dp[i-][r]%mod;
if(!num)continue;
dp[i][l+r]+=num;if(dp[i][l+r]>=mod)dp[i][l+r]-=mod;
dp[i][l+r+]+=num;if(dp[i][l+r+]>=mod)dp[i][l+r+]-=mod;
(dp[i][l+r]+=num*(l+r)*)%=mod;
if(l+r>)
(dp[i][l+r-]+=num*l*r*)%=mod;
if(l+r>)
(dp[i][l+r-]+=num*(l*(l-)+r*(r-)))%=mod;
}
}
cout<<dp[k][]%mod<<endl;
return ;
}
NOIP模拟测试2-5的更多相关文章
- 「题解」NOIP模拟测试题解乱写II（36）
毕竟考得太频繁了于是不可能每次考试都写题解.(我解释个什么劲啊又没有人看) 甚至有的题目都没有改掉.跑过来写题解一方面是总结,另一方面也是放松了. NOIP模拟测试36 T1字符 这题我完全懵逼了.就 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 C. 分组
2019.8.3 [HZOI]NOIP模拟测试12 C. 分组 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 刚看这题觉得很难,于是数据点分治 k只有1和2两种,分别 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 B. 数颜色
2019.8.3 [HZOI]NOIP模拟测试12 B. 数颜色 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 数据结构学傻的做法: 对每种颜色开动态开点线段树直接维 ...
- 2019.8.3 [HZOI]NOIP模拟测试12 A. 斐波那契(fibonacci)
2019.8.3 [HZOI]NOIP模拟测试12 A. 斐波那契(fibonacci) 全场比赛题解:https://pan.baidu.com/s/1eSAMuXk 找规律 找两个节点的lca,需 ...
- NOIP模拟测试17&18
NOIP模拟测试17&18 17-T1 给定一个序列,选取其中一个闭区间,使得其中每个元素可以在重新排列后成为一个等比数列的子序列,问区间最长是? 特判比值为1的情况,预处理比值2~1000的 ...
- NOIP模拟测试1(2017081501)
好,今天是cgg第一次举行模拟测试,希望各位支持. 时间限制:2小时 题目链接: 题目一:水得都没名字了 题目二:车站 题目三:选数 不要觉得2小时太少,我的题目很良心,都很简单. 答案可以在模拟测试 ...
- 「题解」NOIP模拟测试题解乱写I（29-31）
NOIP模拟29(B) T1爬山 简单题,赛时找到了$O(1)$查询的规律于是切了. 从倍增LCA那里借鉴了一点东西:先将a.b抬到同一高度,然后再一起往上爬.所用的步数$×2$就是了. 抬升到同一高 ...
- 2019.8.14 NOIP模拟测试21 反思总结
模拟测试20的还没改完先咕着 各种细节问题=错失190pts T1大约三分钟搞出了式子,迅速码完,T2写了一半的时候怕最后被卡评测滚去交了,然后右端点没有初始化为n…但是这样还有80pts,而我后来还 ...
- 2019.8.9 NOIP模拟测试15 反思总结
日常爆炸,考得一次比一次差XD 可能还是被身体拖慢了学习的进度吧,虽然按理来说没有影响.大家听的我也听过,大家学的我也没有缺勤多少次. 那么果然还是能力问题吗……? 虽然不愿意承认,但显然就是这样.对 ...
- 2019.8.1 NOIP模拟测试11 反思总结
延迟了一天来补一个反思总结 急匆匆赶回来考试,我们这边大家的状态都稍微有一点差,不过最后的成绩总体来看好像还不错XD 其实这次拿分的大都是暴力[?],除了某些专注于某道题的人以及远程爆踩我们的某学车神 ...
随机推荐
- PHP生成唯一ID的方法
PHP自带生成唯一id的函数:uniqid() 它是基于当前时间微秒数的 用法如下: echo uniqid(); //13位的字符串 echo uniqid("php_"); / ...
- Android 横竖屏切换生命周期
默认情况下,屏幕会旋转并且会重新走生命周期. 1. 屏幕不旋转 在AndroidManifest文件中的对应Activity中配置android:screenOrientation=”landsc ...
- github项目上传管理
一.完成项目后再在github上面新建仓库然后上传代码文件 1.创建仓库时不初始化README.md文件 touch README.md //此行可忽略 git init //初始化仓库 git ad ...
- LeetCode_155-Min Stack
栈的实现,多加了一个最小值的获取 class MinStack { public: struct Node { int nNum; int nMinNum; Node* pNext; Node() { ...
- 落谷P3941 入阵曲
题目背景 pdf题面和大样例链接:http://pan.baidu.com/s/1cawM7c 密码:xgxv 丹青千秋酿,一醉解愁肠. 无悔少年枉,只愿壮志狂. 题目描述 小 F 很喜欢数学,但是到 ...
- Java中的接口（什么是接口，接口的好处，具体的使用）
1.什么是接口? 官方概述: 在java语言中,接口不是类,而是对类的一组需求描述,这些类要遵从接口描述的统一格式进行定义. 这种技术主要用来描述类具有什么功能,而并不给出每个类的具体实现. Bala ...
- 渗透测试-基于白名单执行payload--Csc
复现亮神课程 基于白名单执行payload--csc 0x01 Csc.exe C#的在Windows平台下的编译器名称是Csc.exe,如果你的.NET FrameWork SDK安装在C盘,那么你 ...
- Cocos2d-x 学习笔记(11.5) SkewTo SkewBy
1. SkewTo SkewBy node朝X和Y方向的歪斜.SkewTo是SkewBy的父类. 1.1 成员变量 create方法 // 两者成员变量一致 float _skewX; float _ ...
- std::lock_guard 与 std::unique_lock
std::lock_guard 与 std::unique_lock 对 mutex 进行自动加解锁. mutex m; void fun() { unique_lock<mutex> m ...
- Pathon中numpy模块
目录 numpy模块 切割矩阵 矩阵元素替换 矩阵的合并 通过函数创建矩阵 fromstring/fromfunctions 矩阵的运算 常用矩阵运函数 矩阵的点乘 矩阵的逆 矩阵的其他操作 nump ...