[考试反思]1106csp-s模拟测试103： 渺茫

7点之前上不了博客，用gedit写的。谅解一下。

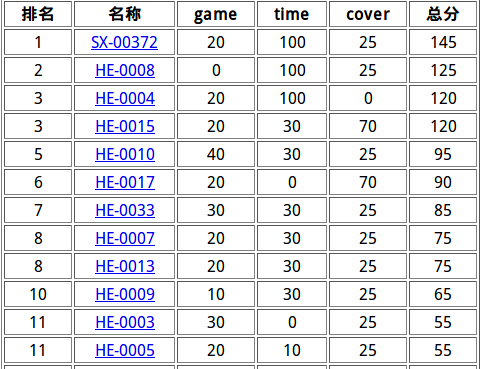
看起来不是特别惨？但是被sdfz爆踩了。。。
而且其实并不能说“不是特别惨”吧
90分算个啥啊？还凑不出个T2的AC
难易度评估错误，T2是最简单的没看出来。然后爆搜不够优秀TLE 0.
T1伪证的60分只有20,如果外层加一个clock就有40.。。
T3部分分打满，很明显了却没有想到启发式合并
说实在的还是经验不足实力不够，面对难题原型毕露（虽说相对于简单题稍微好一些）

T1:Game
先不考虑字典序，如何得到最高的积分？
贪心。这个好说。
但是在后面的操作中还需要修改牌序，导致局面变化，还要统计动态的积分。
就是说，你需要依次考虑每一位应该填什么，然后删除这张牌再check一下看积分变不变。
在积分不变的基础上，这一位越大越好。这满足单调性可以二分（稍后具体讲）
其实这类似于单点修改操作（挺抽象的）。
暴力贪心的话那么就需要从头再重新做一遍。
考虑如何优化？那只能是数据结构了。
线段树分治。（基于值域）
对于A和B有的牌都开一个权值线段树。考虑合并两个子树（即线段树update）操作。
右儿子的A和左儿子的B可以结合（满足大小关系），这些是可以获胜的局面，全局累加答案。
即设$win=min(A_{rc},B_{lc})$。那么在上传的时候，就有$ans+=win,A_p=A_{lc}+A_{rc}-win,B_p=B_{lc}+B_{rc}-win$
就是已经胜利的局面累加积分并且不再参与以后的运算。最后全局ans的值就是最大积分。
这就是最优决策。已经是用尽量小的A去战胜B了，等价于贪心。
单点修改的话直接重置某一个下标的AB值，整条链都修改一下就好。
在修改的时候要注意全局的ans应该要删除原来这个节点的贡献再修改并update，否则积分就会重复计算。
现在说明一下它的单调性（证明二分）：其实并不是直接二分，也不是完全的单调性。
先考虑如果你赢了这一位，那么你用的值越大，得分可能越低（浪费了）
如果你输了这一位，那么你用的值大了，总得分可能也会降低（也是浪费）
如果你可以在赢下这一位的基础上保证总积分不变，那么你就会赢下这一位（因为这样的话字典序会更大）
所以二分的过程其实是：检查这一位能不能赢，如果可以就在$[b_i+1,max]$二分，如果不能赢就在$[1,b_i]$二分
找到最大取值，在线段树里删除，同时也要把B删除。逐位考虑即可。
可以拿multiset维护一下剩余A的最大值作为二分上届。不然有可能被卡常（只有我被卡了。。。）
复杂度$O(nlog^2n)$
%%%Rock_B教我看懂标程
%%%yxs暴力踩暴正解（比正解还难写还需要一大堆特殊性质，咱也不会打%%%就是了）

据说建树容易被卡常，传参好像比建树全局调用快一些。

 #include<cstdio>
 #include<set>
 using namespace std;
 multiset<int>S;
 int n,a[],b[],cl[],cr[],A[],B[];
 int cnta[],cntb[],ans,rans;
 void up(int p){
     int nw=min(B[p<<],A[p<<|]);
     ans+=nw;A[p]=A[p<<]+A[p<<|]-nw;B[p]=B[p<<]+B[p<<|]-nw;
 }
 void build(int p,int l,int r){
     cl[p]=l;cr[p]=r;
     if(l==r){A[p]=cnta[l];B[p]=cntb[l];return;}
     build(p<<,l,l+r>>);build(p<<|,(l+r>>)+,r);
     up(p);
 }
 void modify(int p,int pos){
     if(cl[p]==cr[p]){A[p]=cnta[pos];B[p]=cntb[pos];return;}
     ans-=min(B[p<<],A[p<<|]);
     if(pos<=cr[p<<])modify(p<<,pos);
     else modify(p<<|,pos);
     up(p);
 }
 bool chk(int x,int p,int de){
     cnta[x]--;modify(,x);
     int rA=ans+de;
     cnta[x]++;modify(,x);
     return rA==rans;
 }
 int main(){
     freopen("game.in","r",stdin);freopen("game.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i)scanf("%d",&b[i]),cntb[b[i]]++;
     for(int i=;i<=n;++i)scanf("%d",&a[i]),cnta[a[i]]++,S.insert(a[i]);
     build(,,*(--S.end()));rans=ans;
     for(int i=;i<=n;++i){
         cntb[b[i]]--;modify(,b[i]);
         int l=b[i]+,r=*(--S.end()),ta=;
         while(l<=r)if(chk(l+r>>,i,))ta=l+r>>,l=(l+r>>)+;else r=(l+r>>)-;
         if(!ta){
             int L=,R=b[i];
             while(L<=R)if(chk(L+R>>,i,))ta=L+R>>,L=(L+R>>)+;else R=(L+R>>)-;
         }else rans--;
         cnta[ta]--,modify(,ta);printf("%d ",ta);S.erase(S.find(ta));
     }puts("");
 }

T2：Time
贪心。不能直接做就要去发现特殊元素或特殊性质。
考场上一直以为最大值是特殊元素然后就卡死了。（因为会对其他元素产生影响）
实际上是要考虑最小值。它最后一定在两侧，考虑它是往左还是右移就好了。
如果一个数出现了多次，那么就依次考虑是最左边的数往左移还是最右边的数往右移就好了。

 #include<cstdio>
 #include<vector>
 using namespace std;
 vector<int>v[];
 int n,x[],t[];long long ans;
 void add(int p,int w){for(;p<=n;p+=p&-p)t[p]+=w;}
 int ask(int p,int a=){for(;p;p^=p&-p)a+=t[p];return a;}
 main(){
     freopen("time.in","r",stdin);freopen("time.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i)scanf("%d",&x[i]),v[x[i]].push_back(i),add(i,);
     for(int i=;i<=;++i){
         int h=,t=v[i].size()-;
         while(h<=t){
             int l=ask(v[i][h]-),r=ask(n)-ask(v[i][t]);
             if(l<r)ans+=l,add(v[i][h],-),h++;
             else ans+=r,add(v[i][t],-),t--;
         }
     }printf("%lld\n",ans);
 }

T3：Cover
首先看到“包含或不相交”就知道要建树，有父子关系。建一个超级父节点控制[1,n]避免它是森林。

因为我脑子很清奇所以我的建树比较诡异，所有区间（包括超级根节点）按照l为第一关键字从小到大，r为第二关键字从大到小排序。

这样排序之后，你就得到了这棵树的dfs序，然后根据“dfs序下一个点的子树是一段连续的区间”，用全局的单调指针递归建树即可（详见代码，这个讲不好）
然后尝试dp。
因为我脑子比较清奇所以我并没有像题解一样设出那个dp然后再差分。
我的dp定义是f[i][j]表示对于i这个点，你给它「第」j次覆盖的机会时所得到的「额外」收益。
所以我的dp一设出来就是题解里那个数组的差分。
考虑转移，我给这个点一次覆盖机会，那么它的决策要么是把机会下传给所有儿子，要么是就用来覆盖自己这个区间
那么$f[i][j]=\sum f[son][j]$。在这样得到f数组之后它是单调的（你会采取最优决策来让它收益最大化,最优决策一定会在第一次被取出，以此类推）
所以f[p][1]>=f[p][2]>=f[p][3]...然而这样并没有考虑这个点本身。
所以在这个本身已经有序的数组里插入$w_p$就好了。然后超级根节点的f数组前缀和一下就是答案。
那25的部分分就不需要维护有序数组，而是直接开桶，把“倒深度”放进去再做前缀和就好了。
因为除了叶节点以外，一个点的子树大小一定大于自身大小，所以有覆盖机会就下传就好了。
给出暴力代码。

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 using namespace std;
 vector<long long>v[];
 struct P{
     int l,r,w,o;
     friend bool operator<(P a,P b){
         return a.l<b.l||(a.l==b.l&&a.r>b.r)||(a.l==b.l&&a.r==b.r&&a.o>b.o);
     }
 }ps[];
 long long ans,Ans[];int n,m,sz[],l[],to[],cnt,fir[],ald=,spj=;
 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;}
 void dfs(int p){
     for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]);
     sz[p]++;v[p].resize(sz[p]);
     for(int i=fir[p];i;i=l[i])for(int j=;j<sz[to[i]];++j)v[p][j]+=v[to[i]][j];
     v[p][sz[p]-]=ps[p].w;
     sort(v[p].begin(),v[p].end());reverse(v[p].begin(),v[p].end());
 }
 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-);}
 int DFS(int p){
     int dep=;
     for(int i=fir[p];i;i=l[i])dep=max(dep,DFS(to[i])+);
     Ans[dep]+=ps[p].w;
     return dep;
 }
 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].o=i,ps[i].r--;
     m++;ps[m]=(P){,n,,m};
     for(int i=;i<m;++i)if(ps[i].w!=ps[].w)spj=;
     sort(ps+,ps++m);build();
     if(spj){DFS();for(int i=;i<m;++i)Ans[i]+=Ans[i-],printf("%lld ",Ans[i]);return ;}
     dfs();
     v[].resize(m);
     for(int i=;i<m;++i)ans+=v[][i-],printf("%lld ",ans);puts("");
 }

TLE70

如果用数组维护，时空都无法接受，考虑用数据结构。
需要支持的操作：插入一个值，不断取出最大值。（然后删除，这样次大值就变成了最大值，就可以依次取出并加和了）
大根堆。优先队列。
然而就这样空间对了时间复杂度还是有问题。
启发式合并，把重儿子的队列直接接过来，然后再与其它儿子合并。
复杂度$O(nlog^2n)$，并不知道是不是正解复杂度（为什么出了300000？）

update：我又害人了我写挂了，复杂度写成$O(n^2logn)$了。

 #include<cstdio>
 #include<algorithm>
 #include<queue>
 using namespace std;
 priority_queue<long long>v[],r;
 struct P{
     int l,r,w;
     friend bool operator<(P a,P b){
         return a.l<b.l||(a.l==b.l&&a.r>b.r);
     }
 }ps[];
 long long ans,Ans[];int n,m,sz[],l[],to[],cnt,fir[],ald=,spj=;
 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;}
 void dfs(int p){
     for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]);
     sz[p]++;
     for(int i=fir[p];i;i=l[i])if(sz[to[i]]+==sz[p]){swap(v[p],v[to[i]]);to[i]=;break;}
     for(int i=fir[p];i;i=l[i])if(to[i]){
         while(!v[to[i]].empty())r.push(v[p].top()+v[to[i]].top()),v[p].pop(),v[to[i]].pop();
         swap(r,v[p]);while(!r.empty())v[p].push(r.top()),r.pop();
     }v[p].push(ps[p].w);
 }
 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-);}
 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].r--;
     m++;ps[m]=(P){,n,};
     sort(ps+,ps++m);build();
     dfs();
     for(int i=;i<=m;++i)v[].push();
     for(int i=;i<m;++i)ans+=v[].top(),v[].pop(),printf("%lld ",ans);
 }

错的

 #include<cstdio>
 #include<algorithm>
 #include<queue>
 using namespace std;
 priority_queue<long long>v[],r;
 struct P{
     int l,r,w;
     friend bool operator<(P a,P b){
         return a.l<b.l||(a.l==b.l&&a.r>b.r);
     }
 }ps[];
 long long ans,Ans[];int n,m,sz[],l[],to[],cnt,fir[],ald=,spj=;
 void link(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;}
 void dfs(int p){
     for(int i=fir[p];i;i=l[i])dfs(to[i]),sz[p]=max(sz[p],sz[to[i]]);
     sz[p]++;
     for(int i=fir[p];i;i=l[i])if(sz[to[i]]+==sz[p]){swap(v[p],v[to[i]]);to[i]=;break;}
     for(int i=fir[p];i;i=l[i])if(to[i]){
         while(!v[to[i]].empty())r.push(v[p].top()+v[to[i]].top()),v[p].pop(),v[to[i]].pop();
         while(!r.empty())v[p].push(r.top()),r.pop();
     }v[p].push(ps[p].w);
 }
 void build(int p){while(ps[p].l<=ps[ald].l&&ps[ald].r<=ps[p].r)link(p,ald),ald++,build(ald-);}
 int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;++i)scanf("%d%d%d",&ps[i].l,&ps[i].r,&ps[i].w),ps[i].r--;
     m++;ps[m]=(P){,n,};
     sort(ps+,ps++m);build();
     dfs();
     for(int i=;i<=m;++i)v[].push();
     for(int i=;i<m;++i)ans+=v[].top(),v[].pop(),printf("%lld ",ans);
 }

对的