《机器学习技法》---AdaBoost算法

1 AdaBoost的推导

首先，直接给出AdaBoost算法的核心思想是：在原数据集上经过取样，来生成不同的弱分类器，最终再把这些弱分类器聚合起来。

关键问题有如下几个：

（1）取样怎样用数学方式表达出来；

（2）每次取样依据什么准则；

（3）最后怎么聚合这些弱分类器。

首先我们看第一个问题，如何表示取样？答案使用原数据集上的加权error。

假设我们对数据集D做的取样如下：

那么我们在新数据集上的01error可以等效为在原数据集上的加权error：

即我们取样相当于确定一组权重μ，对这个加权的error作最小化就能得到一个弱分类器g。

特别的，对于svm和逻辑回归，如果我们已知权重μ，我们可以用下面的方式解：

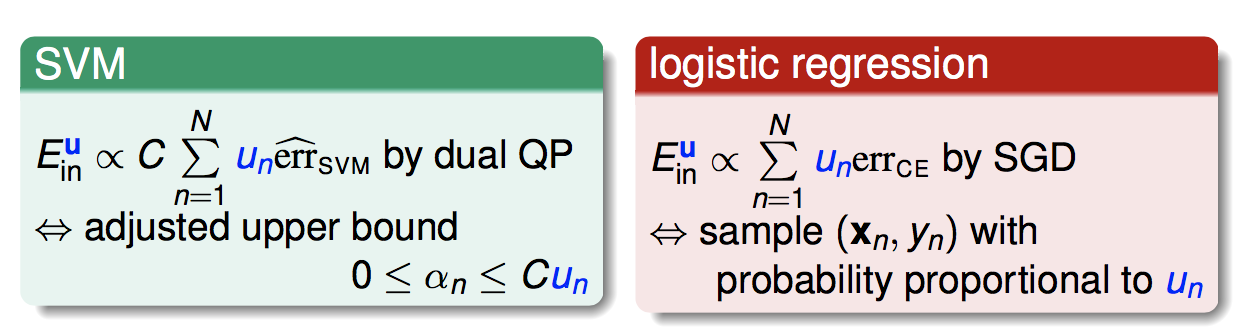
然后是第二个问题，依据什么原则来取样？或者说，怎样选择权重μ。

答案是多样性。即保证生成的每个弱分类器的差别越大，最后的聚合出来的强分类器就会越好。

如何来保证这一点呢？假设我的第t次取样生成了gt，第t+1次取样生成了g(t+1)，取样的规则分别是μt和μt+1。即：

那么，要保证gt+1和gt有很大不同，有一个办法，就是使gt用在gt+1的数据集上时，效果很差。效果很差就是错误率是0.5，跟扔硬币一样：

即：

所以，更新这个权重的方法是，对于t轮上分类错误的点，它的u应该更新为乘以总的分类正确率，对于分类正确的点，它的u应该更新为乘以总的分类错误率，注意这里的分类错误率是加权后的分类错误率（或者说在采样后的分类错误率）：

这里我们使用另一种与上面等效的方法：

它有一定的物理意义：由于上一轮错误率总是小于0.5，因此方块t是大于1的。因此对于上一次分类正确的权重，除以方块t，减小了权重；对于上一次分类错误的权重，乘以方块t，放大了权重。

类似于水果课堂中老师教学生的例子。

第三个问题，得到了这些弱分类器，如何把他们聚合起来？AdaBoost使用的是Linear Blending的方式，其中的权重应该与方块t成正比，即这个弱分类器表现越好，权重应该越大：

另外，初始的u我们定为均匀的。

这样，AdaBoost算法如下：

2 AdaBoost的理论保证