STL~heap

1.定义

堆：若将此序列所存储的向量R[1..n]看做是一棵完全二叉树的存储结构，则堆实质上是满足如下性质的完全二叉树

树中任一非叶子结点的关键字均不大于（或不小于）其子结点的关键字。分为大根数（默认）和小根树（自定义cmp)

高度：堆可以被看成是一棵树，结点在堆中的高度可以被定义为从本结点到叶子结点的最长简单下降路径上边的数目；定义堆的高度为树根的高度。我们将看到，堆结构上的一些基本操作的运行时间至多是与树的高度成正比，为O（lgn）。

摘取：http://blog.csdn.net/blade2001/article/details/6901100

STL里面的堆操作一般用到的只有4个。

make_heap();、pop_heap();、push_heap();、sort_heap();

他们的头函数是algorithm

首先是make_heap();

他的函数原型是：

void make_heap(first_pointer,end_pointer,compare_function);

一个参数是数组或向量的头指针，第二个向量是尾指针。第三个参数是比较函数的名字
。在缺省的时候，默认是大跟堆。（下面的参数都一样就不解释了）

作用：把这一段的数组或向量做成一个堆的结构。范围是(first,last)

然后是pop_heap();

它的函数原型是：

void pop_heap(first_pointer,end_pointer,compare_function);

作用：pop_heap()不是真的把最大（最小）的元素从堆中弹出来。而是重新排序堆。它
把first和last交换，然后将[first,last-1)的数据再做成一个堆。

接着是push_heap()

void pushheap(first_pointer,end_pointer,compare_function);

作用：push_heap()假设由[first,last-1)是一个有效的堆，然后，再把堆中的新元素加
进来，做成一个堆。

最后是sort_heap()

void sort_heap(first_pointer,end_pointer,compare_function);

作用是sort_heap对[first,last)中的序列进行排序。它假设这个序列是有效堆。（当然
，经过排序之后就不是一个有效堆了）

 #include<iostream>
 #include<algorithm>
 using namespace std;
 int num[]= {,,,,,};
 void print(int len)
 {
     for(int i=; i<len; i++)
         cout<<num[i]<<" ";
     cout<<endl;
 }
 bool cmp(int a,int b)
 {
     return a>b;
 }
 int main()
 {
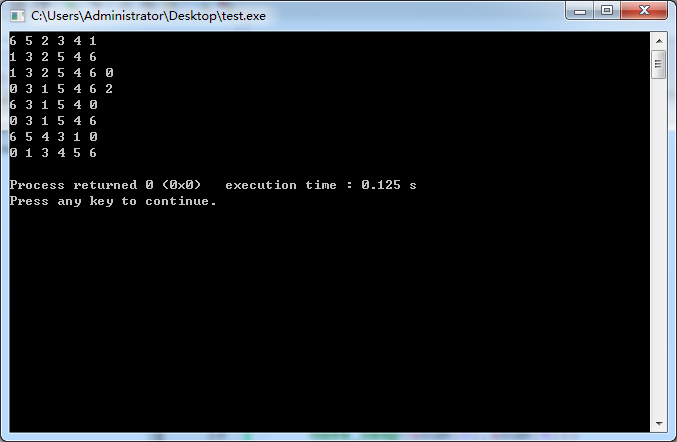
     //*make_heap()
     make_heap(&num[],&num[]);
     print();
     make_heap(&num[],&num[],cmp);
     print();
     //*push_heap()
     num[]=;
     push_heap(&num[],&num[]);
     print();
     push_heap(&num[],&num[],cmp);
     print();

     //*pop_heap
     pop_heap(&num[],&num[]);
     print();
     pop_heap(&num[],&num[],cmp);
     print();
     //*sort_heap
     sort_heap(&num[],&num[],cmp);
     print();
     sort_heap(&num[],&num[]);
     print();

 }