机器学习课程-第8周-聚类(Clustering)—K-Mean算法

1. 聚类(Clustering)

1.1 无监督学习: 简介

在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一个假设函数。与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：

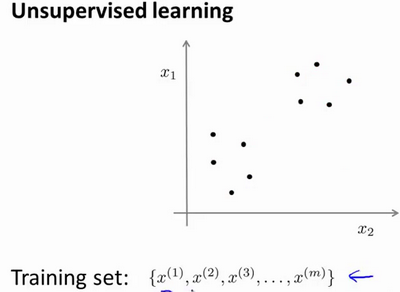
在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成 两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

这将是我们介绍的第一个非监督学习算法。当然，此后我们还将提到其他类型的非监督学习算法，它们可以为我们找到其他类型的结构或者其他的一些模式，而不只是簇。

1.11 聚类算法用途

1.2 K-均值算法

K-均值 是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值 是一个迭代算法，假设我们想要将数据 聚类成n个组，其方法为:

• 首先选择 K 个随机的点，称为聚类中心（cluster centroids）；

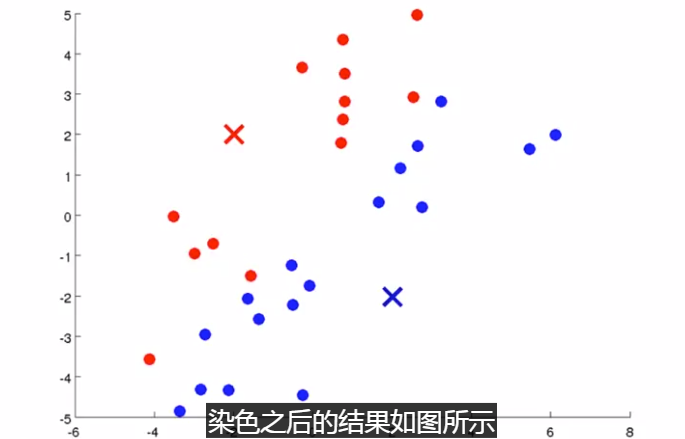
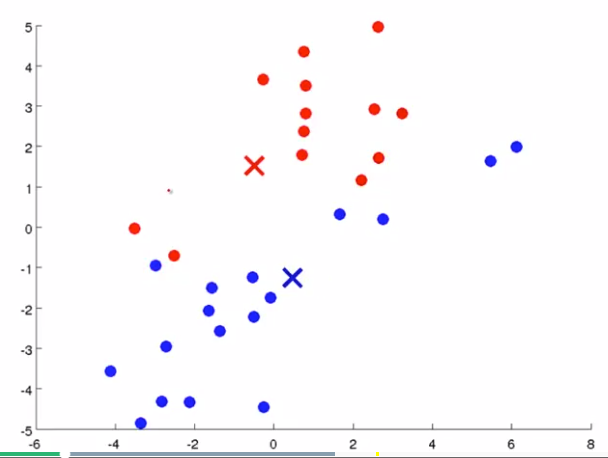
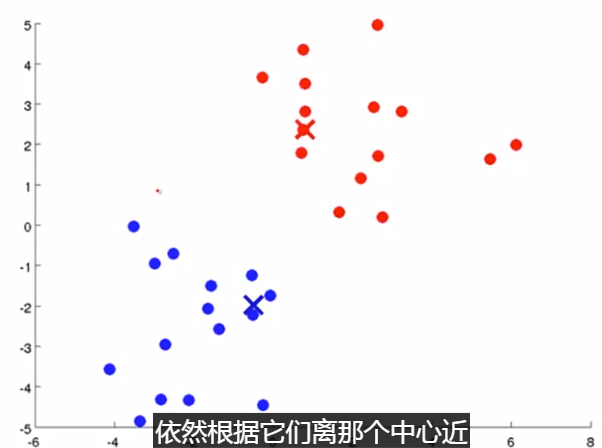
• 簇分配：对于数据集中的每一个数据，按照 距离 K个中心点的距离，将其 与距离最近的中心点 关联起来，与 同一个中心点 关联的所有点聚成一类。

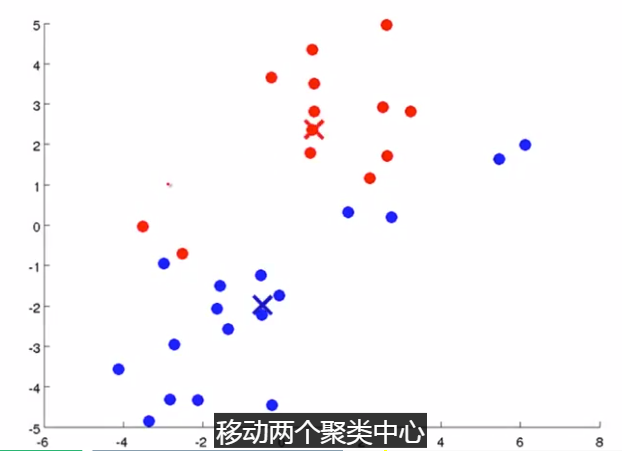
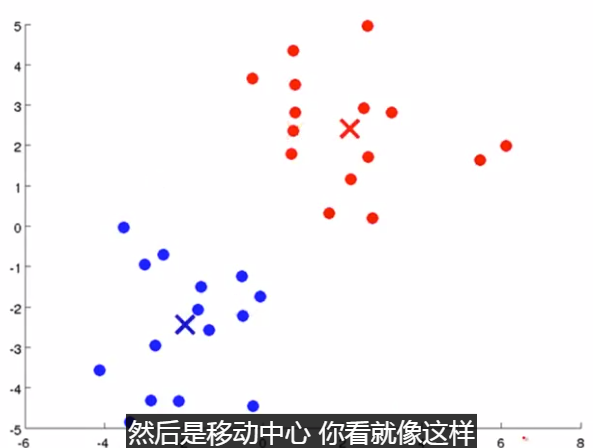
• 移动聚类中心：计算每一个组的平均值，将该组 所关联的中心点 移动到 该组平均值的位置。

• 重复步骤2-4直至中心点不再变化。

下面是一个聚类示例：

                           (簇分配)                                             （移动聚类中心）

重复该步骤。

Repeat {

    for i =  to m   # 簇分配

    　　c(i) := index (form  to K) of cluster centroid closest to x(i)       # 是接近 哪一个聚类中心 k； c(i) = min_k:||x^(i) - u_k||^2

    for k =  to K   # 移动聚类中心

    　　μk := average (mean) of points assigned to cluster k

}

注意：

• 没有分配点的聚类中心直接删除；

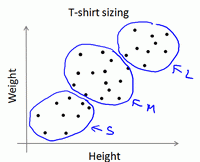
• K-均值算法也可以很便利地用于将数据分为许多不同组，即使在 没有非常明显区分的组群 的情况下也可以。

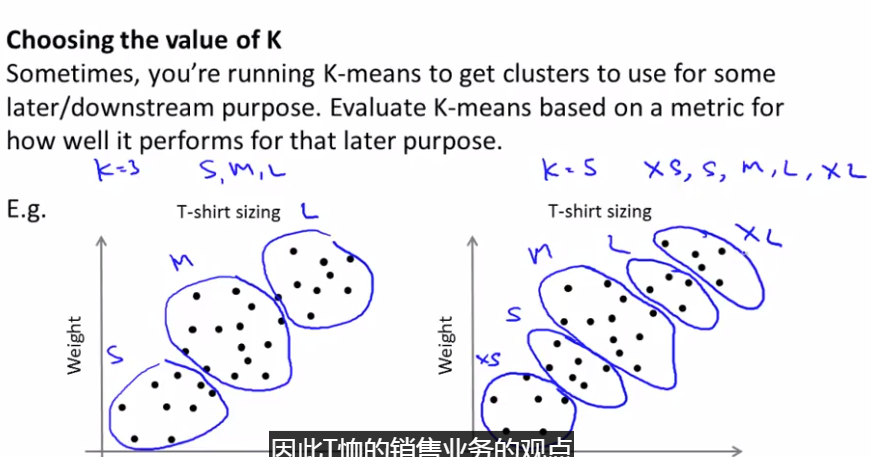
• 下图所示的数据集包含 身高和体重 两项特征构成的，利用K-均值算法将数据分为三类，用于帮助确定将要生产的T-恤衫的三种尺寸。

1.3 优化目标

K-均值最小化问题：最小化 所有的数据点 与 其所关联的聚类中心点 之间的 距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

$$J(c^{(1)},...,c^{(m)},μ_1,...,μ_K)=\dfrac {1}{m}\sum^{m}_{i=1}\left\| X^{\left( i\right) }-\mu_{c^{(i)}}\right\| ^{2}$$

其中 ${{\mu }_{{{c}^{(i)}}}}$ 代表与 ${{x}^{(i)}}$ 最近的聚类中心点。

优化目标：

• 找出使得代价函数最小的 $c^{(1)}$,$c^{(2)}$,...,$c^{(m)}$ 和 $μ^1$,$μ^2$,...,$μ^k$：
• （代价函数会一直变小，不可能上升）

1.4 随机初始化

在运行K-均值算法的之前，我们首先要 随机初始化 所有的聚类中心点，下面介绍怎样做：

1. 我们应该选择 $K<m$，即 聚类中心点的个数 要小于 所有训练集实例的数量
2. 随机选择 $K​$ 个训练实例，然后令 $K​$ 个聚类中心分别与这 $K​$ 个训练实例相等

K-均值 的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

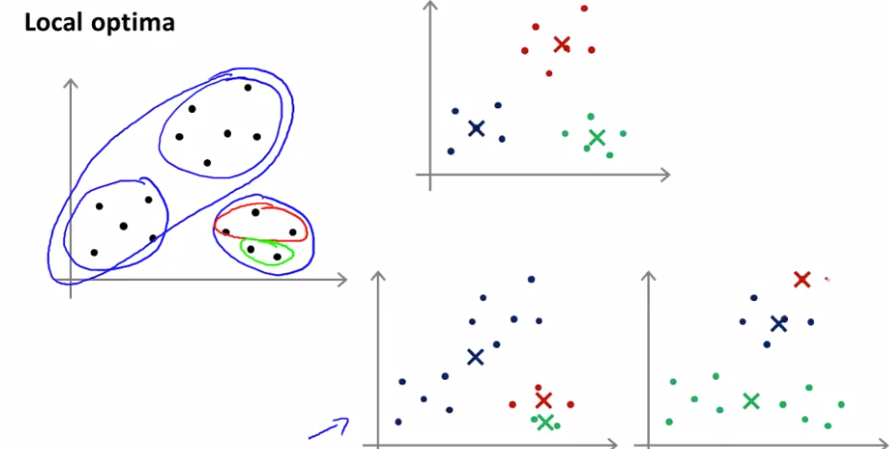
尝试多次随机初始化

1.5 选择聚类数

没有所谓最好的 选择聚类数目 的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用K-均值算法聚类的动机是什么，然后选择能 最好 服务于该目的 的聚类数。

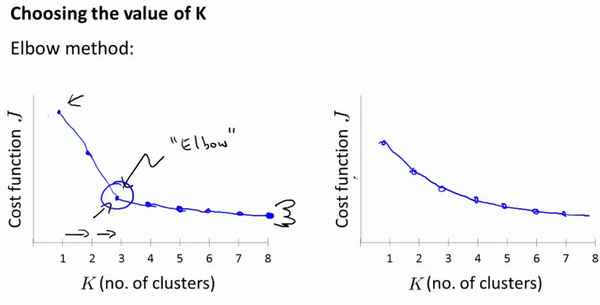
当人们在讨论，选择聚类数目 的方法时， “肘部法则”：

• 改变 K 值，也就是 聚类类别数目的总数。我们用一个聚类来运行 K均值聚类方法。

• 这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数或者计算畸变函数 J 。K 代表聚类数字。