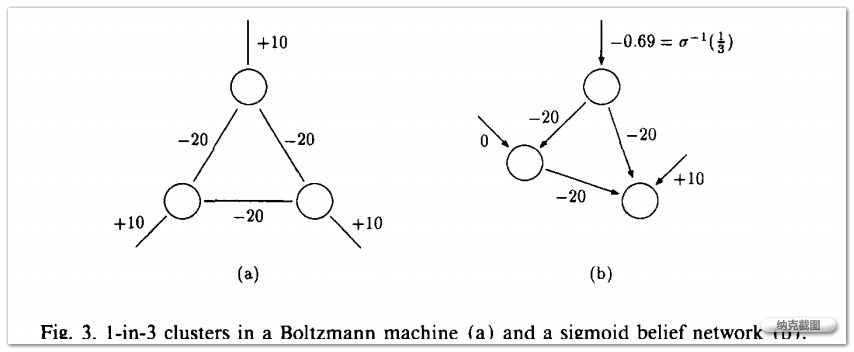
because of explaining away, the hidden weights in sigmoid belief network is no longer independent

sigmoid belief network boltszmann machine的更多相关文章

  1. Deep Belief Network简介

    Deep Belief Network简介 1. 多层神经网络存在的问题 常用的神经网络模型, 一般只包含输入层, 输出层和一个隐藏层: 理论上来说, 隐藏层越多, 模型的表达能力应该越强.但是, 当 ...

  2. Convolutional LSTM Network: A Machine LearningApproach for Precipitation Nowcasting

    Convolutional LSTM Network: A Machine LearningApproach for Precipitation Nowcasting 这篇文章主要是了解方法. 原始文 ...

  3. Deep Belief Network简介——本质上是在做逐层无监督学习，每次学习一层网络结构再逐步加深网络

    from:http://www.cnblogs.com/kemaswill/p/3266026.html 1. 多层神经网络存在的问题 常用的神经网络模型, 一般只包含输入层, 输出层和一个隐藏层: ...

  4. Deep Belief Network

    Deep Belief Network3实例3.1 测试数据按照上例数据,或者新建图片识别数据. 3.2 DBN实例//****************例2(读取固定样本:来源于经典优化算法测试函数S ...

  5. Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.3

    Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.3 http://blog.csdn.net/sunbow0 第二章Deep ...

  6. Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.1

    Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.1 http://blog.csdn.net/sunbow0 Spark ML ...

  7. Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.2

    Spark MLlib Deep Learning Deep Belief Network (深度学习-深度信念网络)2.2 http://blog.csdn.net/sunbow0 第二章Deep ...

  8. Neural Network Virtual Machine

    深度学习Stack 为什么提出NNVM? 深度学习框架现状 - “碎片化” 目前,深度学习应用框架呈现出高度的“碎片化(fragmentation)”倾向,这主要是由于下述两个原因: 1. 深度学习正 ...

  9. 【机器学习Machine Learning】资料大全

    昨天总结了深度学习的资料,今天把机器学习的资料也总结一下(友情提示:有些网站需要"科学上网"^_^) 推荐几本好书: 1.Pattern Recognition and Machi ...

随机推荐

  1. go 多态

    demo1 // Sample program to show how polymorphic behavior with interfaces. package main import ( &quo ...

  2. VC.【转】采用_beginthread/_beginthreadex函数创建多线程

    https://blog.csdn.net/cbnotes/article/details/8331632 还可以看这个网址的内容:[多线程]VC6使用_beginthread开启多线程的方法-技术宅 ...

  3. STL——set

    (转) 1.关于set C++ STL 之所以得到广泛的赞誉,也被很多人使用,不只是提供了像vector, string, list等方便的容器,更重要的是STL封装了许多复杂的数据结构算法和大量常用 ...

  4. 《剑指offer》第五十五题（二叉树的深度）

    // 面试题55(一):二叉树的深度 // 题目:输入一棵二叉树的根结点,求该树的深度.从根结点到叶结点依次经过的 // 结点(含根.叶结点)形成树的一条路径,最长路径的长度为树的深度. //如果左右 ...

  5. 学习笔记4-pathon的range()函数和list()函数

    使用python的人都知道range()函数很方便,今天再用到他的时候发现了很多以前看到过但是忘记的细节.这里记录一下range(),复习下list的slide,最后分析一个好玩儿的冒泡程序. 这里记 ...

  6. 04-python-闭包

    1.闭包的概念: 官方概念:在一些语言中,在函数中可以(嵌套)定义另一个函数时,如果内部的函数引用了外部的函数的变量,则可能产生闭包.闭包可以用来在一个函数与一组"私有"变量之间创 ...

  7. 最新省市区数据，sql插入语句

    --省数据 insert into Province (ProvinceName)  values('北京市'); insert into Province (ProvinceName)  value ...

  8. redflag的echarts结构

    总体的市场情况 这里我需要4个data数组. var list = { currentData:[],//这里表示当月数据量,数组长度8 totalData:[],//这里表示的累计数据量,数组长度8 ...

  9. Enable SMB2 on the Client

    HKEY_LOCAL_MACHINE\System\CurrentControlSet\Services\LanmanWorkstation edit DependOnService and add ...

  10. Feign二：复写Feign的默认配置

    Feign二:复写Feign的默认配置 1.在启动文件加入feign注解:@EnableFeignClients FeignApp.java import org.springframework.bo ...