POJ 1179 - Polygon - [区间DP]

题目链接：http://poj.org/problem?id=1179

Time Limit: 1000MS Memory Limit: 10000K

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N. 

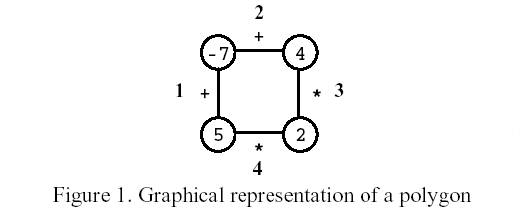
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 
pick an edge E and the two vertices V1 and V2 that are linked by E; and 
replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.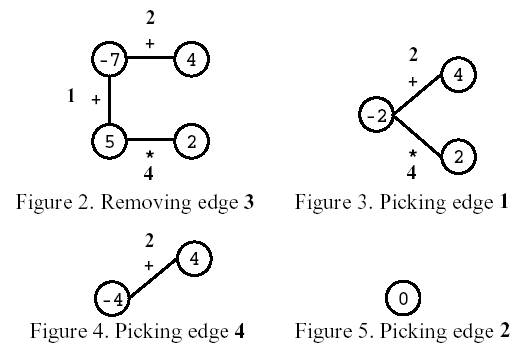 

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50 
For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

题意：

给出一个由无向边和节点组成的环，每个节点上有一个数字，每条边上有一个运算符（加或乘），

现在先割断一条边，然后环就成为一个链，然后你每次可以将这条链上的一条边缩成一个点，产生的新点的权值就是两个节点配合边运算所产生的结果。

不停地缩边成点，直到最后只有一个点为止，求这个点的权值最大是多少。

并给出所有能产生这个最大值的首先割断的边的编号，要求从小到大输出。

题解：

区间DP，周赛上wyb出的毒瘤题，每次两个小区间合并的时候，要记得有可能两个最小的负数相乘可能会产生正数最大值。

因此需要同时维护区间最小值和最大值。

AC代码：

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int maxn=;
 
int n;
int op[*maxn],nm[*maxn];
pii dp[*maxn][*maxn];
inline int calc(int type,int a,int b){return type?a*b:a+b;}
inline void updatemn(int &x,int y){if(x>y) x=y;}
int solve(int l,int r)
{
    for(int s=;s<=r-l+;s++)
    {
        for(int st=l,ed=st+s-;ed<=r;st++,ed++)
        {
            dp[st][ed].first=-INF;
            dp[st][ed].second=INF;
            for(int mid=st+;mid<=ed;mid++)
            {
                pii le=dp[st][mid-];
                pii ri=dp[mid][ed];
 
                int tmp1=calc(op[mid],le.first,ri.first);
                dp[st][ed].first=max(dp[st][ed].first,tmp1);
                dp[st][ed].second=min(dp[st][ed].second,tmp1);
 
                int tmp2=calc(op[mid],le.first,ri.second);
                dp[st][ed].first=max(dp[st][ed].first,tmp2);
                dp[st][ed].second=min(dp[st][ed].second,tmp2);
 
                int tmp3=calc(op[mid],le.second,ri.first);
                dp[st][ed].first=max(dp[st][ed].first,tmp3);
                dp[st][ed].second=min(dp[st][ed].second,tmp3);
 
                int tmp4=calc(op[mid],le.second,ri.second);
                dp[st][ed].first=max(dp[st][ed].first,tmp4);
                dp[st][ed].second=min(dp[st][ed].second,tmp4);
            }
        }
    }
    return dp[l][r].first;
}
int main()
{
    scanf("%d",&n);
    for(int i=;i<n;i++)
    {
        int m; char o[];
        scanf("%s",o); op[i]=op[n+i]=(o[]=='x');
        scanf("%d",&m); nm[i]=nm[n+i]=m;
    }
 
    for(int i=;i<*n;i++) dp[i][i]=make_pair(nm[i%n],nm[i%n]);
    int ans=-INF;
    for(int c=;c<n;c++) ans=max(ans,solve(c,c+n-));
 
    vector<int> E;
    for(int c=;c<n;c++) if(dp[c][c+n-].first==ans) E.push_back(c+);
    sort(E.begin(),E.end());
    printf("%d\n",ans);
    for(int i=;i<E.size();i++) printf("%d%c",E[i],(i==E.size()-)?'\n':' ');
}

数据：

x  x  t  t  x 
 
x - t - t - t - x -
 
t  x  t -
 
x  t  x  t  t  x  x  x  x  x  x  t  t  x  t  x  x  t  x  x  t  x  x  x  x  x  t  x  x  x 
 
x  x  x  x - t  x - x - x  t  t - x  t  x  x  t  x  x - x - x  x  t  x  t  x  x  x  t  x  x  x  x  x  x  x - t  x  x - x - t  x  t  x  x  x - t  t - t - x