Asp.Net MVC4中的全局过滤器

可以对整个项目进行全局监控。

新建一个MVC4项目，可以在global.asax文件中看到如下代码：  FilterConfig.RegisterGlobalFilters(GlobalFilters.Filters);

表示注册全局过滤器.

GlobalFilters是全局过滤器的集合，可以通过add方法添加过滤器，默认情况下，HandleErrorAttribute过滤器被添加到集合中。

接下来我们创建一个自定义过滤器，然后添加到全局过滤器集合中。

1.创建自定义过滤器

创建自定义过滤器要继承ActionFilterAttribute类。我们创建一个名称为CustomerFilterAttribute的过滤器，在action里面记录下时间。

代码如下:

public class CustomerFilterAttribute : ActionFilterAttribute
  {  

      public override void OnActionExecuting(ActionExecutingContext filterContext)
      {
          base.OnActionExecuting(filterContext);
          filterContext.HttpContext.Response.Write("开始时间:"+DateTime.Now.ToString()+"<br/>");
      }  

      public override void OnActionExecuted(ActionExecutedContext filterContext)
      {
          base.OnActionExecuted(filterContext);
          var controllerName = filterContext.RouteData.Values["controller"].ToString();
          var actionName = filterContext.RouteData.Values["action"].ToString();  

          filterContext.HttpContext.Response.Write("结束时间:" + DateTime.Now.ToString() + "<br/>");
          filterContext.HttpContext.Response.Write("controller:" +controllerName+",action:"+actionName);
      }
  }

　　

　　　　　　2.注册全局过滤器

过滤器创建完成后，我们把这个过滤器添加到全局过滤器中，使用  filters.Add(new CustomerFilterAttribute());方法，

代码如下:

public class FilterConfig
   {
       public static void RegisterGlobalFilters(GlobalFilterCollection filters)
       {
           filters.Add(new HandleErrorAttribute());
           filters.Add(new CustomerFilterAttribute());
       }
   }

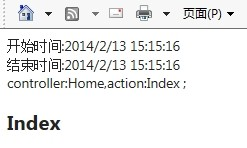
　　  接下来我们运行项目中的每一个页面，都会看到页面中输出时间和controller名称，效果图如下: