BZOJ.3884.上帝与集合的正确用法(扩展欧拉定理)

\(Description\)

　　给定p，

　　

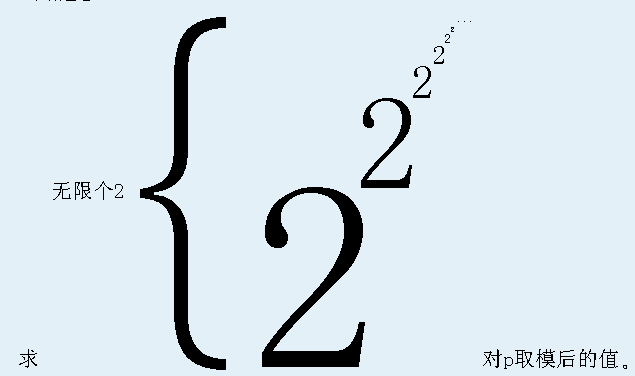
\(Solution\)

　　欧拉定理：\(若(a,p)=1\),则\(a^b\equiv a^{b\%\varphi(p)}(mod\ p)\).

　　扩展欧拉定理：\(a^b\equiv a^{b\%\varphi(p)+\varphi(p)}(mod\ p)\) (a为任意整数，b,p为正整数，且\(b>\varphi(p)\)（a,p不一定要互质）.证明.

　　指数是无穷的，但是模数是有限的，从不断减小p去考虑。

　　设\(f(p)=2^{2^{2^{...}}}mod\ p\)，次数是无穷的，所以肯定\(>p\)。根据扩展欧拉定理可得

\[\begin{aligned} f(p)&=2^{2^{2^{...}}mod \varphi(p)+\varphi(p)}(mod\ p)\\&=2^{f(\varphi(p))+\varphi(p)}(mod\ p)\end{aligned}
\]

　　这样就有了f的递推式，可以直接递归计算。

　　那么复杂度是多少？

　　若\(p\)为偶数，则\(\varphi(p)\leq\frac{p}{2}\)；若\(p\)为奇数，则\(\varphi(p)\)为偶数，转化为偶数的情况。所以最多递归\(log_2p\)层。

　　\(n>2时,\varphi(n)始终为偶数\)的一个证明：

　　设\(n=\prod p_i^{a_i}\)，则\(\varphi(n)=\prod (p_i^{a_i}-p_i^{a_i-1})\).

　　若\(n=2^a,a\geq 2\)，则\(\varphi(n)=2^a-2^{a-1}=2^{a-1}(2-1)\)，为偶数。

　　否则，若\(n>2\)，且至少有一个奇素数p，则\(p_a-p_{a-1}(a\geq 1)\)为偶数（因为两个数都是奇数）。

　　另官方题解.

#include<cstdio>
#include<cstring>
typedef long long LL;
const int N=1e7+3,M=10005;

int p,val[N],P[M+3],cnt;
bool NP[M+3];

void Init()
{
	for(int i=2;i<M;++i)
	{
		if(!NP[i]) P[++cnt]=i;
		for(int j=1;j<=cnt&&i*P[j]<M;++j)
		{
			NP[i*P[j]]=1;
			if(!(i%P[j])) break;
		}
	}
}
int FP(LL x,int k,LL p)
{
	LL t=1;
	for(;k;k>>=1,x=x*x%p)
		if(k&1) t=t*x%p;
	return t;
}
int Get_Phi(int n)//O(sqrt(n))求单值欧拉函数
{
	LL res=1;int mod=n;
	for(int t,i=1;i<=cnt&&P[i]*P[i]<=n;++i)
		if(!(n%P[i]))
		{
			n/=P[i], (res*=(P[i]-1))%=mod;
			while(!(n%P[i])) n/=P[i],(res*=P[i])%=mod;
		}
	if(n>1) (res*=n-1)%=mod;//别忘n本身可能是个质数
	return res;
}
int Calc(int n)
{
	if(val[n]!=-1) return val[n];
	int t=Get_Phi(n);
	return val[n]=FP(2,Calc(t)+t,n);
}

int main()
{
	Init();
	int t; memset(val,0xff,sizeof val), val[1]=0;
	for(scanf("%d",&t);t--;)
	{
		scanf("%d",&p);
		printf("%d\n",Calc(p));
	}
	return 0;
}