[LeetCode] 23. Merge k Sorted Lists ☆☆☆☆☆

转载:https://leetcode.windliang.cc/leetCode-23-Merge-k-Sorted-Lists.html

描述

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

Example:

Input:
[
1->4->5,
1->3->4,
2->6
]
Output: 1->1->2->3->4->4->5->6

k 个有序链表的合并。

我们用 N 表示链表的总长度，考虑最坏情况，k 个链表的长度相等，都为 n 。

解法一 暴力破解

简单粗暴，遍历所有的链表，将数字存到一个数组里，然后用快速排序，最后再将排序好的数组存到一个链表里。

public ListNode mergeKLists(ListNode[] lists) {
    List<Integer> l = new ArrayList<Integer>();
    //存到数组
    for (ListNode ln : lists) {
        while (ln != null) {
            l.add(ln.val);
            ln = ln.next;
        }
    }
    //数组排序
    Collections.sort(l);
    //存到链表
    ListNode head = new ListNode(0);
    ListNode h = head;
    for (int i : l) {
        ListNode t = new ListNode(i);
        h.next = t;
        h = h.next;
    }
    h.next = null;
    return head.next;
}

时间复杂度：假设 N 是所有的数字个数，存到数组是 O（N），排序如果是用快速排序就是 O(Nlog_N)，存到链表是 O（N），所以取个最大的，就是 O(Nlog_N)。

空间复杂度：新建了一个链表，O（N）。

解法二 一列一列比较

我们可以一列一列的比较，将最小的一个存到一个新的链表里。

public ListNode mergeKLists(ListNode[] lists) {
    int min_index = 0;
    ListNode head = new ListNode(0);
    ListNode h = head;
    while (true) {
        boolean isBreak = true;//标记是否遍历完所有链表
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < lists.length; i++) {
            if (lists[i] != null) {
                //找出最小下标
                if (lists[i].val < min) {
                    min_index = i;
                    min = lists[i].val;
                }
                //存在一个链表不为空，标记改完 false
                isBreak = false;
            }

        }
        if (isBreak) {
            break;
        }
        //加到新链表中
        ListNode a = new ListNode(lists[min_index].val);
        h.next = a;
        h = h.next;
        //链表后移一个元素
        lists[min_index] = lists[min_index].next;
    }
    h.next = null;
    return head.next;
}

时间复杂度：假设最长的链表长度是 n ，那么 while 循环将循环 n 次。假设链表列表里有 k 个链表，for 循环执行 k 次，所以时间复杂度是 O（kn）。

空间复杂度：N 表示最终链表的长度，则为 O（N）。

其实我们不需要创建一个新链表保存，我们只需要改变得到的最小结点的指向就可以了。

public ListNode mergeKLists(ListNode[] lists) {
    int min_index = 0;
    ListNode head = new ListNode(0);
    ListNode h = head;
    while (true) {
        boolean isBreak = true;
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < lists.length; i++) {
            if (lists[i] != null) {
                if (lists[i].val < min) {
                    min_index = i;
                    min = lists[i].val;
                }
                isBreak = false;
            }

        }
        if (isBreak) {
            break;
        }
        //最小的节点接过来
        h.next = lists[min_index];
        h = h.next;
        lists[min_index] = lists[min_index].next;
    }
    h.next = null;
    return head.next;
}

时间复杂度：假设最长的链表长度是 n ，那么 while 循环将循环 n 次。假设链表列表里有 k 个链表，for 循环执行 k 次，所以时间复杂度是 O（kn）。

空间复杂度：O（1）。

解法三 优先队列

解法二中，我们每次都是取出一个最小的，然后加入一个新的， O（1）的复杂度，再找最小的，O（k） 的复杂度。我们完全可以用一个优先队列。

我们将优先级定义为数越小优先级越高，如果用堆实现优先队列，这样我们每次找最小不再需要 O（k），而是 O（log（k）），当然这样的话，我们加入新的话不再是 O（1），也需要 O（log（k））。可以看看这里和这里。

public ListNode mergeKLists(ListNode[] lists) {
        //定义优先队列的比较器
        Comparator<ListNode> cmp;
        cmp = new Comparator<ListNode>() {
        @Override
        public int compare(ListNode o1, ListNode o2) {
            // TODO Auto-generated method stub
            return o1.val-o2.val;
        }
        };

        //建立队列
        Queue<ListNode> q = new PriorityQueue<ListNode>(cmp);
        for(ListNode l : lists){
            if(l!=null){
                q.add(l);
            }
        }
        ListNode head = new ListNode(0);
        ListNode point = head;
        while(!q.isEmpty()){
            //出队列
            point.next = q.poll();
            point = point.next;
            //判断当前链表是否为空，不为空就将新元素入队
            ListNode next = point.next;
            if(next!=null){
                q.add(next);
            }
        }
        return head.next;
    }

时间复杂度：while 循环依旧取决于最长的链表长度 n，while 循环里边，如果有 k 个链表，入队出队都需要 log（k），除此之外还有初始化队列的时间复杂度 O（k）。所以时间复杂度是 O（min（k，nlog（k）））。

空间复杂度：优先队列需要 O（k）的复杂度。

解法四 两两合并

利用之前合并两个链表的算法，我们直接两两合并，第 0 个和第 1 个链表合并，新生成的再和第 2 个链表合并，新生成的再和第 3 个链表合并...直到全部合并完。

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode h = new ListNode(0);
    ListNode ans=h;
    while (l1 != null && l2 != null) {
        if (l1.val < l2.val) {
            h.next = l1;
            h = h.next;
            l1 = l1.next;
        } else {
            h.next = l2;
            h = h.next;
            l2 = l2.next;
        }
    }
    if(l1==null){
        h.next=l2;
    }
    if(l2==null){
        h.next=l1;
    }
    return ans.next;
}
public ListNode mergeKLists(ListNode[] lists) {
    if(lists.length==1){
        return lists[0];
    }
    if(lists.length==0){
        return null;
    }
    ListNode head = mergeTwoLists(lists[0],lists[1]);
    for (int i = 2; i < lists.length; i++) {
        head = mergeTwoLists(head,lists[i]);
    }
    return head;
}

时间复杂度：不妨假设是 k 个链表并且长度相同，链表总长度为 N，那么第一次合并就是 N/k 和 N/k ，第二次合并就是 2 * N/k 和 N/k，第三次合并就是 3 * N/k 和 N / k，总共进行 n - 1 次合并，每次合并的时间复杂度是 O（n），所以总时间复杂度就是O(\sum_{i=1}^{k-1}(i*\frac{N}{k}+\frac{N}{k}))=O(kN)O(∑​i=1​k−1​​(i∗​k​​N​​+​k​​N​​))=O(kN)，可以将两项分开，N/k 其实是常数，分开的第一项是等差数列。

空间复杂度：O（1）。

解法五 两两合并优化

依旧假设是 k 个链表，合并的过程优化下，使得只需要合并 log（k）次。

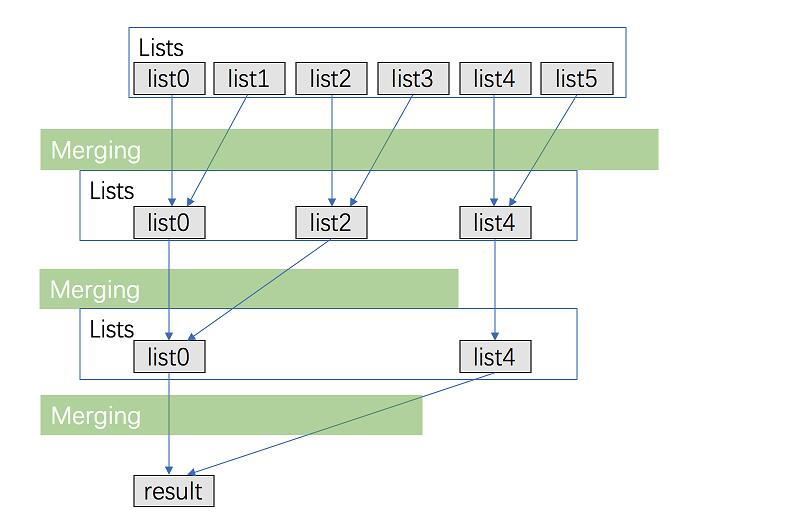
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode h = new ListNode(0);
    ListNode ans=h;
    while (l1 != null && l2 != null) {
        if (l1.val < l2.val) {
            h.next = l1;
            h = h.next;
            l1 = l1.next;
        } else {
            h.next = l2;
            h = h.next;
            l2 = l2.next;
        }
    }
    if(l1==null){
        h.next=l2;
    }
    if(l2==null){
        h.next=l1;
    }
    return ans.next;
}
public ListNode mergeKLists(ListNode[] lists) {
    if(lists.length==0){
        return null;
    }
    int interval = 1;
    while(interval<lists.length){
        System.out.println(lists.length);
        for (int i = 0; i + interval< lists.length; i=i+interval*2) {
            lists[i]=mergeTwoLists(lists[i],lists[i+interval]);
        }
        interval*=2;
    }

    return lists[0];
}

时间复杂度：假设每个链表的长度都是 n ，那么时间复杂度就是O(\sum_{i=1}^{log_2k}n)=O(nlogk)O(∑​i=1​log​2​​k​​n)=O(nlogk)。

空间复杂度：O（1）。

总结

优先队列的运用印象深刻，此外对两两链表的合并，我们仅仅改变了合并的方式就将时间复杂度降低了很多，美妙！