[Python] 01 - Number
故事背景
一、大纲
如下,chapter4 是个概览,之后才是具体讲解。
二、 编译过程
Ref: http://www.dsf.unica.it/~fiore/LearningPython.pdf
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAt8AAAD+CAIAAABtB/4pAACipUlEQVR4nOzdB0AT1x8H8JA9CTtsSNgbFAUUVNxbVByt27p3p7WuWkf7b6ttbZ1t3dZR957gwC0CogKy9x4hELL5vySaIssgIwF+n7/lH47L5d3du7vvvXt3wd+pvo0BAAAAANAaeE0XAAAAAADgHZBOAAAAAKBdIJ0AAAAAQLtAOgEAAACAdoF0AgAAAADtAukEAAAAANoF0gkAAAAAtAukEwAAAABol/rTye3Td0pyi9u4KAAAAADobIzMjYJCgmoNrD+dnN91ziPQsxgCCgAAAABajZG54b3z99VNJ8IqoU8fb89Az9YvGAAAAAA6qZi7MU+uP607vMF+J1KJtDXLAwAAAIDOrqGwAb1iAQAAAKBdIJ0AAAAAQLtAOgEAAACAdoF0AgAAAADtAukEAAAAANoF0gkAAAAAtAukEwAAAABoF0gnAAAAANAukE4AAAAAoF0gnQAAAABAu0A6AQAAAIB2gXTSAQVW//dljzo6OsoX1dXVNcdp0nA1R1b+2oITVH+4SotMUP2RVUNaaoLqDK/5uS0yQTVHrqkNZrPulNuyMterDSpzUzclNSfYpIm0ZWVWDVRzU2qkVBE6dzGgA4F0AgAAAADtAukEaIuXL15E3L1bUVE5cNAgD08PTRcHqOvRw4fx8fFYLNbOzs4/IAC9aIMPPXfmzP17979Y/pWRkVEbfFwnFPv8+YvYWIFAaGllGRgURCaTP2w6ycnJ32/YuHjpEi9v75YtIejYIJ0ArXDo4MGf//ejVCrF4/Hm5uaQTtqRrz7/QiQW6zGZGRkZc+bNW/rpsnpHE4vFpaWlJiYmzf9EmUx25fKVxNevcThc86cG6rX119/u3rnD1NMrKyvr16/ftp07mvR29C60LdPp9GtXrt4KD+83oD+kE9AkkE6A5uVk52z/Y5ubm9vuPX/j0QEHD9Wy3SgpKcnLy1uybOnCxYsXL1h47MiR2XPnUKnUWqOhs/BPZsxcvXbN8BEjmv+hKMUmJCRYWVkxmczmTw3UVVVVFR8f3yc4+I8d29etWfvP4cNJSUkODg5qvv333347fer00X+Po3QyfuIECwuL/gMHtGqBQccDhwGgeTk5OUVFRXPnz0P7MuWQ6upqoVAY9ewZOh3v2tXX3sEeDbwXEYHFYv0DArKzs2OfP/f398fo6Dx6+LCrr++rly85dnZoJ5iSkvLk0SNjE1bffn3R2du9e/eEAkHffv309fU1OosdVnxcnI6OjqOTE/pJZ9AJRCKXy71z+7aLi6st2xatPrRqzM3Njx09VlxUhGIoGt/ZxQUNf/zoEYPBQMc/EomkmloFr+Lxo4do/Q4cPNjY2BhFkNiY57Ycto+PD16RWUtLSyOfPuXxeNlZWQMHDUT1ASWV6KiohPh4dw8PD0/PevvwgqbKysys4PHQmkInC1bW1miIRCx+nZCQmprau08feRfUO3etbWwcHB0e3LtvZGSExWGfPnnq6eXp4ur66MHDC+cviEWiyCdPegQGolVjZGyEAmtMdLRMJjMxMXlw/769I6oyTo8fPiotKx00aBCVRkMfkZmZiTZntBMIDg4mUyiaXgZAwyCdAM3T1dWlUalhN29+PGkSkUhEQ0RC4bq1a2+FhWNxOLQrPHTkHyNDw+VffOnp7YXSydnTZ7b8/POdexFxcXGL5i8YN3785UuX9h86hHaLP/7wA4o1Y8eN8/D0QH9KTUlBv96/d+/Hn3+GqwCtAZ1ho3hhbW2Njiu3wsPHhoaWlpR8vuzT5StWWNtM3bFt293bd8aEhp47exaNduL4cV1dRkVF5eeffiqTSlEkXbFq5dRp05STysvL+/qr5Y8ePGCxWD2DgsJvhm3ZvNnAwCAzI2PjD9+PCgnJzsr+bNmy3JwcWbVMIpGgAxx61+6du3bt2EGhUtGKPnX2jK2trSYXR0eRnpZeUVHh6OSo3HxQ7kfpf8VXy+/fv3/56pXcvLz5c+euWfctm8P+7NNPrSwt0cjoxMDG1vbQP4d37tiekpyMVty2P7a5e3p+umSpt49Pj549v9+4qbKiAk8gJCcnkYik/gMGoPON3Nxc8Q/i8RMnoIj52dJlIpGouLj48y+/mD13rqaXAdAwSCdA8+zs7fr0Db54/sLG9etXrl6NAsq5c+cuX7y0becOdAY2d/YcdH7m08UHnTGjs2M0ftzLlwaGhixTUxRKMIpemb9u/Y1fxUdv7xkY+M2qVegkft2aNej0+ui/x48fO3bh3Hm016PA2VgrQGfGfD7/k+kzKisrx0+YsGjJkoKCAnT6i36WlJSgaDJs+PDZc2bfuHYNnT3v+vsvlBHHjw1ls21/+OmnJQsX3rsboUwnYrF404YNsTEx23ftRGu5sLBw808/TZs5Y/To0RPGjb925QqazvcbNxYWFOw7dPDq5cvbfv8DHS/RqkcBaOHiRX7+/qgMUc+eQTppEYlJieisICcn59vVa17Exv60ZbNUKk1NTbGzs6PSaPGvXqFxXFxcuFxuUWEhU1d3x5+7f9vyC8ou/KqqeQsWPHzwcNbs2R9NnlRcVFReXu7q5ioUCFCsFAgEf+/be/TI0WNHjhgYGmz+9ZeZ02ekp6ehcdat/Ral0i1bf1v+xRcRdyMgnQBIJ0Dz0BHr2+++y8/LP3L4H3t7h0lTJv+1a7dP1y4BPXrEPn+ORkA7L3Qyh45/zi7OaAeXkZnp4uKMxWIT4hPQGfnm33719PREJ14of6zbsB6dtKWlpd25fWfsuHHomHcv4h7aORIIBE3PZQeEDmAvX7xER6lJU6ccOnDw4cOH6BiGogmNRpNJpY8fPS7n8ULGjMbh8enp6WNCx6JVE3bjZnpa2tJPlyUlJia+Tpw1Z7ZyUq8TEq5cuvzFV1/2CQ5Gk0Xn3zo6OhM/+ohIIKDVik7N0ehXLl9esWolm81OTEzS1dU1tzD/8fsfKFTqiJEj0QEPVQw3d3fNLpCOAS3/mKhoPAG/c9t2tOQ3bNrYu0+f4uJitA0OGzEcbUqvX782NDQ0NTOLj4tD40+aMgWtFHQCwGDQTUxMoiIj0brz8PJiMBgRd++iqSmv5aGteMLHH7l7eIj27yeTyfMXLHidmCgSCm3Z7JjoaLSl/7L1N/QRqEahPYCmlwHQPEgnQCswmcyft2wZNnjw1SuXA3rIe5ZM/PgjtI/LyspCezdbtq2yf4Orm1tRUVF+fr6/v79QKExNTUU7PmdnZ25Z2dOnT7v7+enp6aGpxb16hU7cjx45cvLECfTXr1aswENP21aAjljo5HjEqJEoRhgZGS2YO+92+K3+AwfQ6HQUUy6cO9e9e3d7B4eE+HgUHZycnTGKzkMymWzNqtUEPH7AoIGTp05VTur2rVskMjkwKAitZTTys8hITy8vtDbR9AsKCrr7db93N4JKpfr5+6MRkpOSzMzMUAaKiooq53JDRo5Ciejrb76xt7fX6PLoIFAiQWGid+8+KJdM/njSubPnRoaE5GRno3ihzH+vXr0yYZmgrHn18hUqjdalaxe0Tl/ExqKcgaIk+iva3DgcNhoz8fVrlGY4HE5WZhY6uwgICEAnDMlJyWg6dAYj6XUiqicuLq4Xz59Hq3Xd2m9xWGyfvsEzPvlE08sAaB7ssoG2MDYxtrC0EApFaM+IdnZW1jZoYHRUFIlEcnNzP3v6jAmLhXaI6LhVUlzs7unJ5/NTU1L6DeiPzsNKS0qKCgvNzM2UD9vIzspGP1etXuXl7WNlbYVGaOQBoOCDZaRn8Hg8dHTByB/ZKV/y6AhEJBJRqkjPSH/86PHGTZvQwSkhIQH9VEaHrOwsdNr9v59/trW1sbC0VHUGQiudTqcr78FB6SQ3N8/L2xv9FZ2mV1ZUdPX1vX/vHkonLBMTLpeblZmJkk1paSn6U8+gwKXLlpmbmxvCg09aCEr2Bfn5g4YMRovU0cnxdcJrtEbQSkQbl6OjI4oXCfEJPXr0QKsjLu4Vg8FA6zE3N7esrMzTS37hFY1vaCS/8IqRP8ToJUNXF6WWmzduoI3a0clJfnaRl9d/4ED017i4OLTGUdBEZyPoszZ+v8nOzs7axga6iAEMpBOgcSKRqIrPZ+rpPXv2LDUlddyECcoO/CKREO3Irl29FtirF9rZ5ebmGBoYyKTSE//+i3ZzDg4OaB+HDlTu7u7orAuHx6N9JQorEokEnbfp6uqiKZApFAdHB7QzRePDrRytISM9DR23nF2c0Zo6uH8/iiCBQYFoODqxDr8ZZmBo0KtPb/QrOldGa0eZHtCqQWvE1MzUxtZWKBSqjkNoOK+8PC8vDx3q0FEQTUogEKLhRw7/Y2Vt3TMw8FZ4uFQmE4nF4eHhKBI5O7tQyGSUhCorKt0UdQCdhcNRrUXk5uSgqOGkuA9LsUjlyR5tXCjlowR5/epVdCZgr7i7OO7lK1MWC4XRqMhItCGjgag+ZGdnWVlZYRQpMykpyc6Og9bmq1dxRkZGJiYmz2NiCgsLXVxcUDVISU62tbWlUClo7QuqqlDERDkGDYf1CDCQToDGPX78eN6s2foGBmiXZ2dvP3vuHH19fTMLC3mXAgoFZYoVK78hkUgovjx68HDMqBB0iEL7MnTkux0ejvaeyr0kektQ716XL14aGxIyZOjQYcOHW1hYrPhqOTpkoryy66+/0Pm6pme0A4qOjkE/58+ZW15ejlbWph9+MDM3R0NMTU3RkHkLFyhvEUd/Qr9+/eVXf2zfNmLkqIvnL8yYMtXcwgKN9vv2bcpJDRo8+Mg/RxbMnWfCYh05fgzFkUsXL6alpsTHJ2zYuMHY2Njf3x+t32mTp6CzbRRAbdm2qM706RuM4suIocNQNJk3f17ImDEaXBodRkx0DMoHyitxygttaPGibMHn8xfOm89gMNBwlCqKi4tz8/JGjBiBxlE+LBhlDvSaRCJHPo3csO67yVOncMvKBgwciN6YlpKCUiz6a0J8PDpb8PL2qqysRInHz98fhZ6hw4edPnVq5vQZlpYWBgYGu//+W9PLAGgepBOgYeZm5gsWL0In3w72DvLGZEWM2P3XnxfOn6fTaMNHjEQn4mintuKbb86ePoN2auaWlq9evESHKDaHs2LlSmcXFzQ+Oodet369l7d3fl4e2t+hs+1diilIJFJfX19lUwpocQMHDjQ3N0MvLCwtfbt1Y7FYGMWj0spKy1CemPjRR8rR0FFKJpPqYLF0BiMwKHDH7t33Iu5SqNTevXurJuXTpcuff/8VHhaGDk4ozSxf8bWzs1NJScnqtd+6urlWV1cr+jhL0MRRIrkVFu7q5oZqxfIVKxwcHFNSkq2srP0DAjSyEDoeF1eXlatXK9fmmLFj0WaFTg/GhoZWVvIZDPrAQYNQcPT28UYhY+GiRV26dlG8xfXzL79EmyTaEjds2njxwkX0LiKJNG/B/IAePaplsvEfTbRStIrZsjnfrFppbWOD1unU6dO9fXzQekTb7G752g8nk0l9goM1vQCAVoB0AjSMY8dZsHCh8rXq+guHw1mydGnN0dDuD/1Tdh/x9JRf3kaHw27du6tG0NfX/2TWLFX/EnlvWcWZnPJX6HfSGnoE9kT/MDW+JxYdsc6dOYNyIcoNqge56unpLVn23+Pt+wT3Qf8w764UdNxChzH0TzkcvRcdujA1qgQ67E2bMV35ms1mK19QqVQUfWAtt6xevXv3UgRHtDwDg4LQP4yiAWzJsqXKgbPmzFGO+cnsWcqFH9y3rypVoMChzBzoNRpTuVImT5mi/GtAjwD07+103tyxhcPhevTsif5hGvhObNAJQToBALSYP3ft+v23rUOGDR0TOlbTZQEAtGOQTgAALcbe3mHajBkLFy/64K+0BQAADKQTAEAL6jegP/qn6VIAANo9SCcAAAAA0C6QTgAAbaqoqLigoIBfVVUtkzGZTAeHNw94LeNyCwsKKVQqg05jMBjQOxKAzgzSCQCgVYhEosLCopycnLz8Aj0mMzCwh3J4UlLytes3MIq7Nhwd7FXpJPF14pWr15WhxNraasrkj5XDBQKBRCIhkUjwZUkAdB6QTgAALabmA1ujo2NQ2sAoUoiVlaUqnRgbG6FQQqPRUBAxMTFRvZfJZNra2vAr+QKhwMjov6fnRUXHhIXdYrFMUGRxdnJCP9twhgAAmgHpBADQXGKxOCcnN+H1az6/auSIYcr2D0tL+dNgjeVfucIyNzNTjWxnx0H/MHUeT+Lo6ID+yWSyqqoqDOa/yzoioZBIJGZn56CPEAlFkE4A6AwgnQAAmqW0tPTkqTOFhUUoo5DJ5JKePQwNDTCK59lPmzoJBYsmTQ2LxVKp1JpDevQI8Pb2QtNPSUlVXQZCySYs7Bb66ePjXbOhBQDQMUA6AQA0mbLZQ9lGQqFQBAIBiURyd3P18HDX09NTjoNyBhqIafYjXAkEgq6CssVFqbKy8sXLl1xu+eMnTx3s7fr172toYNCcTwEAaBVIJwCAJkBRo6Sk5MnTZygTcDjyJ8qTyeTQsaP19PTJZFKrfnTNu3hQJBo+bGhUdExqamp6Rma1DJ5hD0CHAukEAKAuHo/36PGTqKgYPp9fUlJsa2uDxWLRcDNFt5K2/JobHA5nh9IRh11YWFRYWKi8lqQsYWUln6X45sg2KwwAoMVBOgEAqCs5OeX+/YfowO/s5NijR4DGE4Dirh9jlEWUv8pksoh791+8eOXj4xUU2BOepg9A+wXpBADQmJpdTJycHL0zs9zd3GxsrJStJloFFVUkFCMoQiUmJoWMGmlubvb+twEAtA+kEwBAg6RS6YuXr/T19GxsrDGK3h4jRwzDtO1FHPXhcLiRI4e5ubmEh9/mVfCUfXIBAO0RpBMAQP34fP7Nm+Exz2NZLJMpkz9G0UTTJXo/HR0de3s7Cwvz4uISVWcUAEC7A+kEAFCP8vLyf0+cys7OIZFIXp6e7esp8ihIWVpaqH4NC7tlZm7m7OSo8Y4yAAA1QToBrQKddm/99Tcut0x1PKh5LaDegR8+vBpTXFy8as1qK2vrFpyFTg6FEiKRaGRkOGrUCAtz8/Z7XE9JSbn/4CEOhw0KCgrw747Hw05P7tnTyH//Pa76teYm1vjm1jLbbJ0dgurXekfAYnHTpk9zcnZWd/ZA+wcbKmgVIpHowvnzCxYuJBDe1LHWSyey6urV36x89erl4qVLR44aBXdqtAiUTkJGjUBHBTqdpumyNIutrW2PAL+HDx+Hh9+qquIPHNBf0yXSCmlpaSnJyWNDQ5W/ank6ObD/QF7eIEgnnQqkE9CKQsePU/VMbMV0IpNtXL8hqE/fHdt23Ll1+8vlX9nY2rbgXHQeaEm+fp1kZW1JVXQxYTAYmi5RC8BisX369GYy9W7fuQvPk62JzeGMnzhR+VrL08m1q9eaMGOgQ4B0AjoCdASyd3S0d3C8e/vWtClT5y1YMHTYUDKZTCQS2+8liTaGosnTp5E3boY7OjqMHRNSd4Sqqioej6d83RrHLVSAstJSdH7c4qsMVY8uXbzZbFs9PWbLThkA0EognYCOg0anDxg8JC0lZdvvv1+/du2zLz63ZbMpZLIWPplD26CgEBn57PqNmzJZNcvEpN5xLl64sHH9BqKie2xrpBNEIBCEjB79xfKvWrzZBn2ogYG+6nOLioqZTN321dW3k6tWwDRwN7t8IJyGdCyQTkCHgoIIx95+5px5t25enztr9ux584YOHcJkMtFxCBpRGsHnV926fRft4fv0DurRw7/ecSQSSXDfvl99/TWmddJJVVXV/DlzHjx4MCE09JtVq/wDAlqpB2t6Rua//550cnQYOnQwDodrjY8ALata0ZWtSiDANFCd8Gg9Nu3LsIG2g3QCOiAKlTp4+MikxNd7/vzzwb178xcusHdwIJPJOGhEaQCNRg0dO7qgoMDXt6tmm5pGjQ1NS01dsXzF4CGD58yba2hoqKPQgh8hlUrRMS4qOobOoPfuFQRNa+1AdTWvoqKkpBRTXzrB43HoDERDJQOtBdIJ6JjQPsvB0cnMzPx2+M0lCxfNmjNn+MgRdBoNnY5DI0q92Gxb9A+j6efAYnG4Lr7dbNjsm1ev3Jsc8fmXX3b3606hUFqwHYXDth00aOC5cxcePHhkbm7m5OjYUlMGrYdXjtJJCaZ2/ZRHE+hO1CFBOgEdGUNXd+iIUcmJiTt37LgXEbHk02W2NjZkRU8UyCgYxcWU3Lw8tq2tVi0NVBgjI+PQiR/HxkSvWL584ODBs+fMMWGZkEmkFmlHQVPwcHfjlfPy8vOtrKxapMygtSnaTsow76YTlFmZTF3NFQq0IkgnoINDQcTBycnCyur6lUvzZs2eM3/e4MFDdBU9IrHadEhue1Kp9MKFy4mJiYMHD+zSxUfTxakNh8N5d+lqw2ZfPn9+3uzZi5ct6xnYk0altkgjCgooPXr4y2QyuKzTLqBEwuNVlJS+c2UHj4NWk44M0gnoFCgUyvBRo1/Hx+/esfPRg4dz58/n2HHQuXhnPjg9i4qOi4+n0WgsU5amy9IgAwPD8R9Pin4Wuf7bdYOGDJ42Y7qpqSmJSGyRFaeaiEQiQWGoM1cG7VdRUVH6Np2gcInWl64utJp0ZJBOQGeBjj3Orq4WVpbhN24sWbhw1ty5Q4YMptPpeAKhEzahFJeU3Ll9V/Gksl7mZmaaLk5jCASCb3c/Nodz+eKFyCdPFi1dGtAjgNpyPVFKSkquXb/p4uzk7e3VIhMEraGyspJbpriyo2hXg2jS4UE6AZ0Lg6E7fFRIYkL8H1u3Rty589kXX1hYmJNaqENDO8LU1e0Z2CMnJ9fH26tdzLihkfHESVOiI5+uWbly8NChc+bNMzTQJ5JIzb88l5qanpiYlJuTa21tZQAPk9VWAkFVRUWF/JWODp3Wvr9dAagD0gnodBSNKG5W1jbXr1z+ZPr0BYsW9RvQHx2tO9XtPGhm/f26a/b2nKYiEAjd/AM4Do6Xzp2ZM3Pmss8/7969G63Z92F5e3vGx8enpKaFhd0OCRkBT0ABQBtAOgEdgfIh6CKhqEkPBOsV3PfVi9j/bfr+/r17c+fPZ7NtSWRyJ+8qq/0MDQ0nTp769PGjdWvWDBws74nCYrGa0xMFxZFBgwb+vWdfQWEhn1/FYNBbtsAAgA8A6QR0BHQa7dK5szW/S0xJnceVUmnUO7dvv3zx4pvVq7v6+lIp5I79gPOHDx8bmxhz2LbttxMoHo/3C+jB5nCuX7kS+eTJ0s8+69a9m/yZKB/a7GFoaDAudIyRkZGuLqN9tScB0FFBOgHtHooaV2/eUL7+sIeph928eezIMXRSzuVyxWIxFSWUDno7T1FRcVj4LSKROH3aFGNjI00Xpx5SBdWvNZ+RX2utGRmbjPvo48gnj5d//nnImDEzPplpYGhI+qDvfURvsbPjtMwMAABaAqQT0O6hQ4uqA/+HpRMqlSqrllUJhFguVyQSi0QiGg0No6Jz8Y7UE0Umk6FoIpFI3N1cjYwMNV2cetBotOOHD9Vc5o2kExUsDnfsyJEnjx+vWrvWydmJQqHgmvG0PWU2gt4nAGgWpBMA5NAxu7ych36KxWLlD/SPRqWQSKQOc6AqKChISUmlUMg9egRoYeoik8mr164VicU1w4c66QQNj4mKunv3LlptXG45+omyJfGDGlHy8wvu3I2wtbH29e3arJkBADQPpBMA5FAWKefxFMHkzT9FRhEz6DQand4xusrq6+sHB/cWVFVp5zUdLBZrZm6OeTd8qJlOcnNyCAQinkBUXpsTiyRUGoVKoeCa2PqFAlxcXHxBQaGbmyuFQmn+TAEAPgykEwDkUBYpL5efdotVjScSCTqwUSlkTRetxZBIJL/u3WQymaYL0ipEYjG3nCdWkcjXIAooTWpEcXZ2NjC4W1xcnJSU7OHh3qoFBgA0AtIJAHLoWKZKJ/JcgqkmkztOLqmpQ/b2xchbv0TyhhORSFyDSCSi0+TUnAiBgEcB7tLlq/EJr13dXHEddFkBoP0gnYAGKa9tdJL2balMVllRIZVIqqur0dm2povTwtCqzC8oYJmYtNTT37UQSiIoX8orrfKfPGSitSlvMWrSdNzd3eTfHOlgD9EEAA3qsLsq0HxVVVVXr14fMKCfnp6epsvSFqRSFE4kmi5Fq0hJTTt58rSrq8vwYUM6TCffWlCS5vFU/ZolmA9NmWQyWQu/sRmAzgbSCWhMdk7O8eMnJ02aqH7bONBCsbEv0DFbX1+vo17Wwcjbh6QVFRUol8hkMjweD89UA6Bdg3QC3iM3L++fI0fHjwtlMpmaLgv4EAKBICkpiUQiOjk6auGNxC1IKpGIRaJqKrX5kxIKRUVFRWQy2dAQvhcQAA2AdALeLzc3/+SpM2NGj4KA0h6VlpYxdZlkCkU7n8CmnZ5FRd24EdbNt+vgwQM1XRYAOiNIJ0AtWVnZp06fDR07msFgaLosoGnMzEynTZssFIo6ao+T1mBmaorFYpOSU2QyWQe+HAaA1oJ0AtSFAsrx4yc//nhCJ7mLpyOhKGi6FO0Ji2VCp9N5PF5RcbGJsbGmiwNApwPpBDRBdk7OP0eOjQsdq6sLLSigI0NhztraKi8vX1Al0HRZtI5AIOCWlUmlMiqNymQysVhsaUlpNaZaX19fOUJ+fj7KdlQqtbCggEanq/rUo7SHlqeRsRE0R4H3gnTSARUUFKpeq/k1ePUO5/Mra35brFJ2ds6p02dGh4xiMnVbttigNeTk5HK5XHNzM9UXJQI1DR40gNRBv6q6mU6fOrX5x58MjYzwePzIkFGfzJq1/Y8/EhIS9h86iFHc2j1y6LBVa9d07949ZOTIjz7+eMmyZco3oneFh4WdOHPaxMREo3MA2gFIJx3Q3r37Va+bk07QH0QiUd3pZ2Rknj4DfVDah+iYmKdPn/Xv3zfA30/TZWln4FpYQyoqKjh2dn/t3fMiNnbRgoUeiJfnubNnJRIJyispycliicTNza1KINDB6NyPuKdKJ48fP5bJZB31qUKgZUE66YCENSJFc9JJIx+BAsq/J059NHE87MHbxi9btjDo9DGhoarGc3VIpVJlQ5p2fu0faD6BQPDdt9/6+HQZMmwonU5vs89FKURXV9c/IMDD3f1ZZOTQ4cPFYnFmZiabzU5KTKLTaGwOJz4u3sLSMiU1tbSkRN/AoLCwsKSkBBWSX1nZZuUE7RekE/CBMjOzjhw9Pi50DLSgtIG01NSL5y9s2bxlyJAhoePHe3p5UtV4qkdVlaC8nIdR3IHS+mXsgIqKinLz8qytrLT5XvrY58//PXZ804YNIaNHjwkd6+Do2JZfEYXOZ3A4vK2trS5T92XsC5ROYqKjfbt1w2KxQqGQQCBYWVnFxMT0CQ5+8viJT5cuaSkpkjrXiwGoC9IJ+HDK24xHh4yEgNI2hALBmdOnz5096+bmNmr06P4DBphbmDfaMaLaxMRIV5fRUb/RsLXduXvvxYuXo0YO9/Ly1HRZ3qOiouLggQNHjxzp6tt1ZEgISgMsFqu1PzQ+Li4uPn7h4sU4HM7Ty+vFixfDR45AwwYMGoT+WllZgcfhnLw8Hz54qEgnj7r7dc/KzBRUVbV2wUAHAOkENEt6esbpM+fGjgmBR923merq6liFXTt2BAYFjR47xs/fv96v96PT6RMnjBeLxfCkkw9joLiOVlJaqumCqAutaxQF0D8rK6u+/fuNGDnSw9OzNdZ+UmLi3NlzEhMSJk+d0sW3Kxri7e1988bNci43MzND+UVFqDBUGhVVzj1//S0SCiOfRoaOH3/i2PG6fe0BqAvSCWguFFBOnjo9flxoC/ZBQQfg0tJSXV1ddNAVCgRCkajepnWZTMblcpX3NLbURytVVQkO7ttSVlqKV1D2xqnbR0c1pPF+PM3s9IOGp6ak1i1kYWHh6VOnLl644OjkNHbs2JGjQ+pdSgQCofFeRK1EIBBIJBJlZ4iysjL0ot4IVVVVhWaw8dad0pISOoPR9t8dracnX57cMm7NgcVFRfPnzquulil/bamuXTWrivrVRiarTk9Lr1vyzMzMA/v2/3vsuJu724SJHw0cPEidS4Hq0zcwGDN2rIOjg62trTL9eHl779uzNyEhAVONYXM4GPmCKkY/vX188vPzn0VFofJz2Gw9fT30awuWBHRUkE5AC8jJycvJzbPjsJs/qTu3b2/95VcDQ8NnzyItLCw/njRpx/btKCUs/XTZ9JkzVaM9i3z22bJlaMd3/14Eh2O398D+E//+e/rkqcNHj6B95Yxp00aNChk/ccIHFwPlnsyMjNycHB0F5UANppNGbnMQiUQJ8fGHDh6UVcsmTZlSbwJoS6jwc2fNcnV3f3j/Plpx02bOfB4TExsTwzI1/WnLFgOD/7625tMlS4yNjWOioysrKz//8kvvLl0WzJmzYPHioF697kdE7N61a/uuXSgKbNqwISc7u5uf3+q1a9t4XlDaMzE2pjPe6W0qFotfxMaiGqL8VbPpBKPo+9xQ+VHyex7zHBUYnTkMGjK4wflsOkNDw0GDB9UslYurKyrWwwcPbWxtSSQSRv5dRUI9fTlTU9PbYeHOzs44PB5tnnDPDlAHpBPQXEQiYcTwYRy2bYtMDe28YmJidu7evebbtVMmTT539uzZC+dPHP/3+NFjY8eNU3VwQaMV5OcHBQV9s/KbiePGnztzxtvbB8UaHo+H1dHJzcn1bF5HATKZNGf+fLST1WXQqTQatoGjRZulkz9+//3Rg4d1y4kOn939/cZPmBDQowc6AtV6Y2ZmVkVlpZWlRVted1PORWpy8t4DB47+88/uHTvWb9r06WefLVm48NHDh0OGDq05cnp6+p979pw5ffrPXbv2Hz6MzrlfPH+O0kncq1eOit6d//vhBydn519//10jlwPYbNt582bXGqhvYPD3vr1qrvqmDm9qOkHZdN3atZkZmXULz2Kxegf3GRUS0tXXtw0u7REIBBsbm0cPH3T17aaMyCXFxUQiEW1EXbp2PXv6NAqgqBhUKrWosPC9UwMA0gloFrT3GTZ0sIuLcwtOU09Pzz/An0KlWltbdenSVVdX18/Pb8f27Xw+v2b3WzqdHtS7F9oF9wkOfnD/wbDhw9F5OTqqsVim6KhmZm7enDKg3aiDo5OBgb6hgb4uk6nxdHL0yJFaJXRwcBg2YgQ6Ibazs2vo2PMsKjom5vmokcM9PT0an98Wh9ISOg55eXujYOSNftLpllZWOdnZtUbr7ueHFu+gIUP+OXw4IyOja7duYTduoCCSnJLSs2fPnJyc5KSkr77+WnkuriVQYfwDAlS/ajadCASCWtETVQZ3D4/QceP6BPdp5lbQJOhz3dzd9u/dN2vOHOUQoUhEIskv2HX3675vz54uvl3ROBQKVSKBfifg/SCdgA+HzpBQNHFzc1XtN1tqsjpv4fDy4678Z52eE+ivylM0cwvzV69eMXR1vX18YqKjzc0t0Gl3R300KjpDDerVa+JHH/l279b4PKJjmPJhehq51qP8UCyCwylXJXpZt/uLcjRjY+NqmaystNTD03P/3r08Hi8/L8/J2RlFEwqFYmVp2fblb49QHBw2YjjKJa6urijc1xtxWoSJiYmdvX2tgejjAoOCXsS+cHZ+c65CoVJsbW3RCzd395mzPlHeQ2RjY9P2/YdAewTpBHwgAgGPTspdXV1qNiFoivIg1yOw55nTp4uLiv0C/Fs2MGkcOum0srIKGTNm7LhQc3NzdeZO9ahfMqV93E6M4gubzWYwGM+ePkVhBc1mbm4uOrrKqqs1dceRVCpNTExGVd3W1kZr73tCB3sXV1cUSkaFhOgyddug5o8cNWrEyJF1h/cMDOzRs6eqAAsWLlS+QOnzi6++Ur5e9tmnmI61bYJWAukEfAh0Bj982BA3N9c2/lyZTIZOrJVtBujIoXxwQkpKii3bFqO4a2Dzjz+JReLm9IfVTvPmz7e0slLeFdXUOKhtQa2qqgoFEeXFmio+H/3MzspC+ZJlaooOtJ6enufOnbNzcKDSaLZsdmVlZVpqat0z9bYhkUguXLyEFt+cObMYjLZ7Eqv60Ja46X//s+NwCERim50k1Owq3shwVePNOwPhe4uAeiCddEDduvmqXjfnorhYJHoVF1/3q3aIRMKQIYPd3d1attjqePL48aYNG3/7fStG8X2nx44eRadrd27f2bhpExpibW3N1NMrKiy0d3Bo+7K1KkcnJ0zrtNK3MXS83/jddza2trPnzkW/3rlzp2dQUNjNm2wOx1TxQNuu3bpt+O67r7/5Br22sLBAY+7ds2fK1KkorKD128allW8FYjGVStHa7wLE4XCqKykAdCSQTjqgIYMHql43J52gw39qWlqtdILOcYcMGeTh7tZKZ+R0Ot3V1VV5MEBHLBPFtWoymezm7k5QwCp6MCjHLOeWr1/33YQJE4J698Io9tTyHidMplZ1otQgOo1mbm5GIrb10rBls5V3DlOpVLRGlOvLytra2NhYR1GFVFdJOHZ2u3fuxOJwXyxfrhxoZ2eH3uXtI3+cF3rj6rVrd+3YsWn9+sCgoDnz57fxjGAU9w/j8bo4nJamEwA6KkgnoAnkX5g+YliLd4OtydPLa/eev5XTX7VmjXIgOtrt2b8PHav09fVPnDmNXpSWlqHCLFq6RE9PD6fod4lGKy4ufhYZ+fMvW1qpbO0LWiIjRgzDaOLKztfffKP8UEcnp5+2vFkdCxcvxigCx5p161Rj2tvbT5k2Tedt4kSZ+M7t256enqqnsFvb2KzftEkmk2nk+hT6UJaJCQF6cQLQ5iCdAHURCIQhgwe29gUdxZeK4ZQtOqrmdOVA5euanRNVt+0g5VzuxvXrHRwdu/r6YsC7nQDa+JJQzRWn6iWjGljzKknNNYsiyJPHj0+dOPHDjz/WzCJofE11nSGRSHPnztLIRwPQyUE6AWpB0WTwoAFt/9iMhqDDho2NTc3j3PPnz1NTUn/f9ocGSwWaxMTERLfGo/clEsmJ48c/mjTJ2bWte1sDALQNpBPwfujsdtCgAV5entpz94e9g/1f+/bWfDibb7du+w4c0GV2zMecfJjKysr8/AIqlcpimWi6LPVY+umnuBrPYiESiStWrWIymdpTzQAAmgLpBLwHiibDhw3x9PTQhueaqODxeF3ddx7tQFbQnhJqg8ysrH//PWVvbzd+3FgtvOuEWuf5+sq+tNqzEouKiisqK0yMjVv2K/QAAO8F6QQ0RnGHzkCv5n1nDdAUpq78uklZWZn2HO/bl6eRkY8fPx04sJ+/n5+mywJA5wLpBDQIh8MN6N8PnXlruiDgA1Eo8vaksjIupJMPU1xUgn7q6+lruiAAdDqQTkCDKBSKg4M9dAJov1A0MTQ0rK6WCYVCjXzbTntXUFhIJBKZNbruAgDaBuywQIMgl7R3JBJp2tRJsCI/TFWVwEBfXyAU1Ox8DQBoG5BOAOiwVE8TgSs7H4BCIU+bNlkikUCzEwBtD7Y6AABoEEQTADQCNjwAOricnNyMzAw3V1c6XRu/ZRcAAOqCdAJAB3czLDw1NY1Go7u7wTNY1VVeXh4XF29ra6P6xh8AQFuCdAJAB8e2tUlJSU1KTIJ0oj60xK5eu8Fm206Z/LGmywJAZwTpBIAOzt7ePvzWncysLD6fD888VYdMVp2UnIJeODk5arosAHRSkE4A6OBMTIw5HDb6qYUPs9dOFRW89PQMtLicHCGdAKAZkE4A6ODQUXbC+FD0E557oiYcDufp4V7O4zEY0I8YAM2AdAJAx6d86glQE41GGzCgn6ZLAUCnBukEgM6iurpaIBBQKBRNFwQAAN4D0gkAnQKfz7985VppaemM6VPhCWONqKyspNFomi4FAJ0d7KQA6BSwWFxhYVFBQcGruHhPD3dNF0dLlZaW/b1nn5OTw8AB/YlEoqaLA0DnBekEgE6BTCZ17eJ95er1+/cfuDg7EQgETZdI61RXVz9+8rSyspJfyYflA4BmQToBoLNwd3dDR1+xSFxSUspimWi6OFqnqKgoNvYFFov18+sO9zcBoFmQTgDoLCgUyojhw/T0mIimy6KNysq4MpnMwcHeyspK02UBoLODdAJAJ2Jt3azjbkJ8/N6//8YoLoLUHK5saah3YDOH15xyI2/MzMz8oBl6h7293dw5n6CAgsVCwwkAGgbpBIDOSCKRSKUyIrEJvSvc3NwGDBygeK+UX1UlqKqS/xDI/18oFIpEomqZrOb4bZlO0E/LZjd4oOkwmcxaEwcAaASkEwA6nTIu98aNMBwWO2rUCPU7WHh4eqJ/6AVKIsVFJSWlJei/0tIy9KOsrKyCx5NpNJ00B5oTfX19eNI/ANoD0gkAnY6gqiolJVUoFDo5Obq4ODd/gigfkMlkmeau7GDe/kGn6QkDRZNDh4/a29v16xtMJpOa+nYAQGuAdAJaC5FI7N0zUH60UBxMqmUy+SFF8RodTJSHl5bqqaDyYROUiMWGJqymzV57xmKx/Py63b5999r1m+bmZs3vJCv/6mMqVYP9TmoOb1ITiEQiQQuhTAGP70TP+0dL6cqly7dv3Vb+qqPYJqsVMMrNU/XLW63au0j1a70jVFVVBfbu0+SZBO0ZpBPQKnR1dY+fPCGVSlEo4ZbzyrjcslL0Py63HL3i8srL0VEBozXpBMHh8Z3nJlI0pwH+fhnpGWiNVFRWNiud6OionqyqJekEo3ZAkT/g5PHTxMQklK6GDR3cqR6hO2jI4ICePVS/ikSi0lIu2jjLuOXy7ZRbVs4tr6yoqHm1ToPpBA0kkaBZq3PpRFsjaEvo8GBkZIReoL0bkUxWHPuxMowO2t9IpTIpGiqVYrQpndQ7tQ6MSCQOGzYErRQ9vQ+PJmiJ0dCBnULR+D07dYfjcGoFFDqDjvTv31dPT0+d8TsMioLqV6FIhMMTcHicDhYnq8YoNlAZWp5akk4wnWzzBBhIJ6Dt6bTC2bZKi0+wAzMwMGjO/SloWSmSCQWjBXcU1zv8vd/MjN7o4e5mbWWpq6vb+JgAgDYG6QS0qZrRBKOt6aRTZRSMon3rydNIWxsbU1O1O9/oYFTRBKOt6QQNb+gSj7JJQEehs7WaqK/WAoS2E9CWIJ2AtoNVRBOkRfZomFZLJ5g3PXc7i6iomOvXb6KD9EcTxymvxzUOLSU6Ha1Gas0hGK1MJ5j6+qBUVQmuXb9hx2G7urrAMa8hOByOzmDUHKIl6QQNh3u/OwNIJ6CNKFtNaJgPP8w0MlylRSaIBipOqtWYqw7B2dkx9sWLzMysc+cvjg4Z9d6eKAQ8Hl+jAQyj3emkFrFYfP36jZiY5ykpqRwOu2bfC6BCIBBQWm1o66g7sJnDm5pOME28Mwu0R5BOQFuodbat/elE+VsnaUFBK2Z0yMhDh4/k5ubl5ee/N53UXez15oCG8l2Thtcc+METrLmWr1+/GfM8lkgkjhwxDKJJvVD6VHbE0eZ0guAgoHRokE5Aq8PqYOl0enV17c7/GG1PJ53oUjeTyZw4YTxKJ06ODpouS+sSicUEAmH4sCFstq2Gi6KVcDgck/mmj7CWpxOMGh2fQfsF6QS0LmWrCR1Dq/feXS1PJ8pB9c5Xx2NkZIj+YRSzjwiFQhKJ1PHy2bChg7t38zU3N2vO/UodFR6PR9GkCVuHptMJBi7xdFyQTkDrwipgGniySDtIJ52pBUUlIyPz2vUbffv24bDZHWD2y8rKJFKpkaE8exEIBBRNNF0ibUSQRxOmstOVcki7SCdoOFzi6ZAgnQAA3oH2/jHPY3Nz806cOD2gf18fH+92fXqanp5x/sJFEok0Yfw4BoOu6eJoKTwOx1T0N2qP6QSjuB/wfbMI2hlIJwCAd6Dd/cAB/dDePjr6+ZWr1ykUiquri6YL9SGkUumzqOiwsFsCgcDCwrxmzydQC/7tY/zbaTqB63QdD6QTAEBtZDJ52NAhLBYrJSXVwcFe08X5QGKxJC4uXiwWd/HxHjCgH3xRCwDtCKQTAEA9sFhs926+6LhOIBCUQwoLi+h0Wju6C5dMJg0a2D8nJ8/T071dX5wCoBOCdAIAaJDqa3sFAsGJE6fwBHyvoEAHB3ut7Sqbl58fHRUTGNiDTpd3MWEpQLM/AO0OpBMAwPvxKiokEklhUdGJk6ftOOwxY0JUbSpags/nR0TcfxYVrbwXOji4t6ZLBAD4cJBOAADvZ2xkNGfOrIh79549ixaJxVr4FKywsFuRz6LweLy7u5u3t5emiwMAaBZIJwAAtZBIxH59gz093HXePsMGiY9PIJFIVlaWbd+UIpPJeDyeru6bp4d169aVx6vo7udra2OLxWrphScAgJognQAAmsDY2Bjz9gZOgUAQFnartKzM3NzMzdXVzd2VRqW+bwItAH1ucnLK89gXhYWFM6ZPVX4pDIvFGjdujBY26gAAPgCkEwDAB9NxdHKIiorJysrOycnlcGyV6aTFv6io5ncUS6XSAwcP5+cXoIEoi2Rn5yjTCQa+dQWADgTSCQDgA5HJpP79+vYKCoyPT8gvKNDT01MOLygsvHTpqpWVhaUFYk6n0z8spojFYoFAUFxSkpGRaWVpyeGwMYoIgiaLoom7m6u7u7vqK+sAAB0JpBMAQLMQiUQvL09MjSaT3Ny8LAX0GqWTqVMmKe9MLiktzc/PZzAYRAKRRCLp6jKUqUUkEvF4FTKZDMURMplsYKCvnM6jx08iIu6jgWjKPj7eynSC9O3bB30oPMIEgA4M0gkAoIU5OthPnDAuIzMzJyfX1JSluuCSkpxy6fJVlEgIBIK9PWfsmNHK4fHxCVev3aiWyURisYuL89gxIcrhKMGg97JMTExYJjUfWYsSTBvPEQCgjUE6AQC0MCqVisKEo6ODRCKp+b0tdAbD3t6OX8mvrKxUPi1NSSwWS6USCpnC1NOj1uhX6+3l6eriQiIRUUbR2ue/AQBaA6STDihC5249QxvatzdpuDojt/gE1RneshNUf2R1hjT109UZ3uITVGfkD3hjrR2MM8ba2Vz12z1MxJtXvphAX3/V8AjM2wpMVPxTv4StWvdafILvnYhGZvO9BWiluqfmptTQcMiuHQ6kEwAAAABoF0gnAAAAANAukE4AAAAAoF0gnQAAAABAu0A6AQAAAIB2gXQCAAAAAO0C6QQAAAAA2gXSCQAAAAC0C6QTAAAAAGgXSCcAAAAA0C6QTgAAAACgXSCdAAAAAEC7QDoBAAAAgHaBdAIAAAAA7dJgOsETILgAAAAAoBU1FDbqH0qhUSLORZzdda41iwQAAACATs3I3JBMI9cdXn86CV0aWpJfwnZjt3KpAAAAANCp+fTxqTuw/nTSfVD3Vi4MAAAAAED9oHMJAAAAALQLpBMAAAAAaBdIJwAAAADQLpBOAAAAAKBdIJ0AAAAAQLtAOgEAAACAdoF0AgAAAADtAukEAAAAANoF0gkAAAAAtAukkzYhExS9Siqg2TmzKVhNl6UFCEvTozMlHFc7Y43XH3F5UnKG0NzFTRen6aIAjVGjQopLspITxObd2Z22oogK0pNeS8z97fQ0vtUCFVF51vMMMceFbdAa9VJUGp+UKTJ39Wy5da4osIjtwjFs9Q2p0TJLRUIpjkDEvTmgyqQSmUwmkkhxRApJ85u4lJeb+CStBMdyDeDoEd87Nj8nKj4tH2va3Y1jTFBn+jIhv7JKqvpVh0Cm0ggfki0qEk8u/H7HgWSTtXv2fWv33pKqR1T8IpVvaW+l19YrQpIZ8ee0n4+EC4Iu/rtxKKONP/0dorxb32z6eXNM9eQtxw52pWuyKEBj1KiQ4ryTf26ceyymesAvKau6Mtu6hFpAkn/2r01zj0Txg/6XsSFAT9PFAQri9Nu7p/187Hb1gBtHV/dr6R2YpODuyk0//xglGP3DiVMBLbKnFmfc/Xvmln9uioIvH1s3uNX3uI2kExnv2bXjf10/uTu6wsp34EAWQSrkl5XlPHlePu63Y7+4YjBVCT/+cKAydMU6j7Y+MEiKH23ceuR2BRFf/vr661KnEZvCP+1p1tBxWlJ09eDWn2IqSLjyZ09fF1iNPPPbpyPeG/ykZfcvHdl1+fSxJDGnW79APUlB5usXIrt5iz//ukvTYi7dYfQPE8KP/KLb1aSFoglGknTmC49tyR4z9z6eZlfPlzu2IrxV4PSNkdd7RXvYU+S/Vyb8M+Ng1dKvP+lZXy1o/K/NRDTts3ZaxP4vM3tbUVp+6o3TXOVvW1WR/3y/UTBu70wPbT2o166Q9SCYjp0+/eyVL157W3bstdUgPGvUtNk3ry++5d7ZloA2V2CCTe8ZqyOu3M/0dmyFHRjeJGjNrMjDS6J7WrbU1AnWQVNX3b90J9nHpS32uI2kEyyj2/BPbMjRe6KLp8//8jt7kmKoNOPWwUgTxUsJv4iPMWz7VhRR+s7fr5tM+z6MQ0ER6tbvM4JPbds2yneDA6nesePP/X5Yf/rZXzk0jKw0aqv3slOfnx41YJbDew7qOIPg0PlO1OfH/idcsPSbz63wGFlFxM5ZQcu/Mz346yemjb9ZUpabW860sKYq21oESbHZMtMeji2WI/CcEev/zfh8WVaZGINRa6oSXlou38iCRW/+lSUZPzmJy+TYsxSVR8Tn8jC6VFUtePeDav+1hYmzE16XGXb3bIPW+loLUFOVv9XVqroSHpeP0SVp9bWAdytkvUSFCc8qDAfZMTveClOTjJ8TzaV52utry6pswT1S4x/T1ArcRgVTEBdGvq4w626nzlUSCS83hc+0Z1HVLpeMl5NURLPzqnedf9hsSkqjE3im3g5GTdyQml54zHv7nQgzkwskRGsfE9WBH2fdZ7q18iXD58ef6vna41aH1Q2evsTZVhHesAzfvgHmp669KhJh6k8nWAOfGb9a29IUr/Wd+g0zPHUorVCAeV86kROmJxVhqK4uyot2WLpPLz+LYxdPJWHek054kQsWbXP+6a81HEVjiZQbm1DGtHM0VeuKknqqhQWVtrPGuajZYFcWuSVwu82VP6e7N7/5RpQfmVdt29dCeRKm7zP/co1aUOuDav21pfHjovNIHE/71m8+qr0ANVX5W1utqoth9Jn/cx/NFum93q2Q9eKlR6UROIEWbdvOqE0E+Qnp1aYTLdq8lbEBLblHakyTK3BbFUyBn34rj+DuYUl9/6i8G78s/ML658jpnHqPc/URpSfkVZv2q7dN8QNnsyrjbj7RzcuS1pQ3fVDhMe9PJ+mJRRiTgaqLBxJuerKOpdObU1VxaYmAasD47/Mk/Oz8MrwBi0X5L1nJhNxCKY1Frf+TJPxSLo5pSMJixBXFYophzXPw4jIR3UD+p9pl1nez/e+3arFIjNF3NWpoGeNN2DXGxoirJBgTW2P19lKCtOQSjLEjWzX7VeWVGLKhYmVLBTwelqZHrCcLcuOv3cJ6LTB9W6SqrIicavawN22qIl4xl6BvTH7njRJ+SQ4Pa2Ss9062lPAL+ThDXcUiEPPyKgkmevK3SYoid11MYE1bO8/2v1ot5RdlV1EtDOttp6h4ci0a5znalvjflAsqcUZM+XLncsV05jvvkgl5hZUYJpNBrjMtEZ8n5GdHl+l6s9+ehop5+QISi0Gs/4Pe+eubz64oKS7BMi31yO/Oa1k5TtdAMa/1LqJ6CibIvpcmZo9h69Yzy/XPY6O1UVJRxsfr6io+VlxaXEnSV62OOvNVq/LXmE2ZgFsgppoy3kRRYXlRBalONZbw88rEegbMOrPYyDgyQYWQQP9v05Lyy/lEXQa+5juKC8R0U2btbUYmLM+vIrLeLHBUwDIxzYBR3zKoXXXl66KkkmSg/84K5OcX87BM43dWUAN1tR5NXFb1bxqq4tWtkG/fVmPpCZJfpInMxripcRBQkPKKiyopRqbvbBb11tvGFmajW5lMUF7CIxq8W8kb3unV8O7abKRsKmIeT8zLTizUdXB7ZyE19nGN7N/ezlw966XxvX0NtTYoKZ/Hx9EY9c+3tCKjEGNhShWWFZbhDMwZtU/yGqr2SnUrcOvuKt+zIbxTtfg5sa/EZovYdeqlTFhaVomhMfVVrbMV8YeisEEhprWP7g3tScT8UjE/OanMwJ5dXztH3R3am6nVs2nXICyIeyFgfaIosExQmsunmBm8GbWxCtNA4Rtfce9LJ6LC2FwxxdLRUjkPsopHpw4+67scpRNB1s3lmzZvzQ4KO7IimCo/YF4+sGVTkskwH4PEq0f/ySXpYsijN/wy5fX2mbtvCUbvjFvkKp8hUfLGZetTZ/z+VzcGRsqNOPa/ybvusb46fsnmyrjlf0f7bU5d040pq4oL/+evZJxe1bPfrggX//LrWudG8r4g4XF0mdXAcdZqZTJ+xqPbFVZT+lirlU4EBTF5Upod502bhyT/wulH5ZbD5rvIymL3DPzswBPjsbd2Le3NQGPGLZ+16B+Pn14tof+5dd+phxG5YseNG9a6DJj/Y7CprCghhq8fxNHFVaUd+H39wouJFbYzY3ZP91QUWZBza8O+BzxTG2udjLN3igZ8unalJwMr48de2T5727lnDutyf/UvuPL7pF8vRFWxv9vz52o7It6o68JpXVXFlJZGbztyLTI37fqdeJuFe2+Pt6lZ5SpfH1u6//aliGKh44HJ39pMmjenb8HJWRt2ntNfnvaj9f61y1cn+l07tnaAPDrJeMnXNp2IzBKWR9158JI58s7BL4KUG46MHxd2YOPdfAKNVPwi7JaYPVl+GipMCts5dfPJ5MBfk1Z0wdb+oE98Xv2p+quijUeYcvvAdw/4NtYsncyIU0W+29dMDZTPa/L+7T9+fv6197dnwvxL3ywi9sznu6d7vJmT+gsm46XdL9H1czasU4ulxc+P1Z7Hf5ZRr2xuoDbSeMlXvvzpj12vHY6f/m1o6ZVlG375K7HKfebep9PsJLXna/4Iye3/Kj+Z9/jMLzN23Mjy+yH9O8/k0z99tC08Eed74J+fJtHS/v513ZKraSLnJQnbQu0VpZRVpR0/cuE5ll4RdWK/cOzNX2b41qnd9YxDLLv51xfD/8kZuvbA8b5GOGnJ9b1rxx+MMZm29/lMOxJGVpkW/uPFZBydH37iStWYX2/OcFae3AhyH/x5JSYmNmxfZOXEzRf3O8T+tuX7FbdEC3cc2uIq3wiEyQeCN+Su27p8AP71llpVt4fk5K6N809mj/rl6N4uinogzDl5cN9FPsvZRCfh3p0c38/+meKpj2msrr47Y01bVvVvGphGKmQDS4/Ee/mixMDFxVxZUaqSf9+y87Hj3J3j7OucAkoLok//eD0hNe3p6XjW5j07P7VpsN5KuQ0vTEZ9NfDNViZMfXDhwPOkiLDLNyr7XT+6uj9dXmh1dnq11uYh3wbL9nYhpR07ePB0Pp5J4t4PixayB75pZXzPxzW8f1su35DrXy9S7r0TDW1f77Tw1t4jzZlifumr/gfjLcdufbLEW0/eIrqjy+IbgT+e3GYVc/j0qe0XIniDli/ReXzjdWJ4dFGXWZvPTXZWnOk1WO3fEGYde7cCt+6uktz4hlC3aslKU1/k6bp2q7EDQzvDQwdP3CwUlCTeuZDGnLv10E4vnahjW7+78/BMiajrwQ0TbAb8OC/YBt/QnkRWkRa24eCdDDydUh57LFrsPtCiVvapM5vzx5ni69+066SG8owXOQyXbozcY38dPByXHRf7mjb65/C5njovG6owLkn1FP59K+6NxtOJMD+qCCMUHhiz7AQOrY+C109Kup4PJWAEqSee4Ho70f7EeCj6UghjDi2fcMs/bNdstIC4tmnn1nB/2Pqpb86DV86BbOydcvabtgpB2s298aJJBmhViZLuXE9xCvZlxjGoLzdfkYxfuGplFy8mRvjq7IZ5WSGnF3Yz5LEfXlh9JrZ4pbNlQ8WUFt/bdEU65etQD3XCibTo/KErkkErlqjZvCTMiyrGGPYglhbkZOe8PHFi31/F/Q7/OCsAn7n3iemmz/t+9P3ZdXcnXh/KwpEtgtjUYyQiluL42dKp+c8ecCesOTvRWln1SzJj03Qslhvl7Np1nh/89VHc8uH3inmKu4Ek+demLT/f9dufNsibp6TjTJa5btjTf/9ix8QrNxnBI40v5jnoJ5/buY/fe89a3PCv72ZWSDCYd/f4orStGw/gl/243xJblnTvlk7tQzXNccLWKSVhDyo/W/39F9YEYVb4rhyncU7Mx1Tqg2NXxcGLDk3p0ouuWJZR+xbcNF27ZKUrhXf+m9CxXLc3bWYyXsS+VcsKR55YNc+WIE0/nXTlkJMzHctPvX0N5+1LO4/xtEJ1C/vuB/FTr+2r8Vc0rxnXNw0773T8x9ke8nkNtl42ZfJe35eLrKKuRuoHB1pcKvHRz96183JFb8UiiigoezOvDRasMismWcd6gVXtqCnMunO49jx6WMaEPW+gNsq4Lw48Y4zrabynxMEk5+zyy1Vjl6/Ff/31mYIKMQZDf3e+UOU/dFlV+SU5j06erLCwJ+tUO+q9+HfHcWLIkRWS/t8XVFYm/PbXWUGfr/eLvpyQyKuSKUuWtmPjz4mjNm7pxixlv/przd2I4im+tWp3feM4lJ67qDf2S5efNuy/GNdzvPTC35fMPjm1Jl/H24Ykn5EzUzZnzd+waACT5/7qQmjE89wpzvZ4GTfuyKxjhFXL5y2e8cn3GTkyg5xz1wu69TTH3al0N1bWIuGrm5eeiAaw0G+kWlVX8PLaZbyXk+55TKByCUvyD3//1Z+O6y7NsqPKVyCr79T133bdt0Z2Vb262rRl1cCmsTSA0mCFbHAJG2TdzdZxDrFS7qYlJdEHrj2Kyuq5frQ9rfayPzn1IO6P/620x/Ji7kXrGDZcb+cZXAtrcGHWVwMVW5ms4vGR/20mTtszd+zamXMTcmS2iryixk6vzto0bbhsS9xp8oX0fN3qrdkj1x+aa0aU5m1PfLTJyUYPq8bHiTJPN7R/a3C9zGc9CctqcG/f6B4p/dImszk7g9dNP7v39MQtM0xwVAsvd2oYhSjKTua59LAXHA4vTs/3WvXNQl3x872feO3/89KwzeP1G6r2qs8RvLz95J0K3Lq7Slnxi8Z22vVVLUHi82ys9WintzswKTfqu19u2Exfst+WUnpvhfVqboA8c2N9JixdWfrsYuX4w5s+ciI0sifBlj7fO/b3ornfrf7BjCDNOx396GBX69odS2rNZsOb9oHf3GtFZEHKy8xq8y7JVx6aDfvy3Cxc5sVFnF8P3xqvX9ZghaHULfz7VpxKo+lEVJKaKCAOWrX5UpCi7VyStfvX+2y0OySyJ49i7F3MterqbIiVt5sevJRiNWqNp7IrCI6gI6yQ6pl7OIx2eL37GwlrgoOufAHJysOPn0+mB/Q2k4cD++BQTuHFnVJ9n7js/rNn9GUqW2D3TztKXLOrq6Ek5/juvQlesw8MNm+wjJLCE3/8nTFk9d/dmWr0tZFk3/5jdf6Qw8u7G6rXM0dYlJwmxjGrov4+/QxLMXIN/SnB05wmf6/NjJk2GLH7Z0fD1l2PLRzMMsVWSzBGA3pxaPJ4HnezSL/32z2W/OpYXJrAsEve+esW4xbOtZDej8BQzF3kV4tkxad+++1h1x/2vEkBOJazt2nBzZt5CwI8xyyreDShiGSDuXucGPrLSCvJi/sYvLEPq06u4sX/G53ilMaVWhrq2QeF1DMf0oK4yGx97x6KG6lJlsFLzAv3nJOaGMQl+85e2+XNohNlXZi9X/blpmGuFHmLb2qB2NKXrdiXSXNu/TTpjuvx7f1s5RMQZaeX4s3d0Ak7lT1wHuNSL65JfyfF+n33g2r9VVZ8Z/FvL/v/8LXHm3nV9/UxyLwZmTbfPXD0eO6jtTkkU8zdcEro4rlW0vv3MURjR2VzWMMFkxQmJZYZ9/Co062rgXm0YjdQG7FUz4XjKq58W0RhYc6Ek5YsGuUojb2AwVs6sCh15gtDrln58eSA6f9zCR9wmMGuuHbBasqWYNPKJ+fJ+qbZ58Odpnw+2VJ4+Uo13ZxjLq8NwufHNm4mTn/UlSnODVuxL6PXrJXTatfu+sdhWk7d4oGpcHu9b+GZLVd0qLKQ/w1zeHO2IUz+edMx8rRd/ZiS1LBd32Z4b1g5hINOrcoefbbhltd327zk80AwtpY3AowebRi1e7eI1c/nzTKI2nIhR8/fm61Y1O9WXbLbwFH6lxYVmfj6KlZg3p1fl7z0Pb/cjvpmBTr3MSg4+qzgp6lq1lW8ufrLqsFNQxzAxjZUIRtaepK8pKgK4+GcNxUFbzHqyn7XAgNH2zp7ltL48Fsp1i+5UntDhldQEKaxejutkYXZQA2UFT76Y8pt+xN/KNpsCHpO8nWCdnpH37vTq3dtNlg2sbsbtujEz9+dcvnuQV8z+doUFcaV4Tiu5hR1Po7Y8P5NVny8gV3Wql6jzRve27/r3T2SzdB1NhiR2/ifw/cdfl42rb8htlpabdRtDIfIoQbq37uUjmGMHDMqUD5VkrWzLUOUncOXYKjp9Vb7GmpV4NbeVaK9SGMbQt2qhZGUxSRWWARw9JTTFWf99dM+6cTvZ8q7VEpKcwtExr5uyjorLX0cWWji5W759hJovfVcWhQ2d/0dv3U7JpjJxxMUpRfgzP3N37P8G96080Tu7HeipYz38lWRRFRk2G/RMBP5sqYzGXgxtxxj1cgBsXbhG9hf1afRdMLPS8jGGI5UdYnF6nbr4/+mvPy0G1kUv5nm8koqk6LaQnlz6U2Y9DS2yiEkSL7IpflxTzMZnv0t5VMQpJ1bfZNL9PZzexsVKzOfpworTdn9er1Z7+U3DpzI8fpcN+rEyhcFev7ronvaNNijWMZ/cuT7X6hzzn7ipWqAyr/1jee6iALFuRfRasKdPxf6Ud4u17gjM45Tv980K4ihXjbBYKryk7Ixpp+GTltvX19bC8EiZAB79b+RCYL+ppKXZ3kBCxTNmWWJD18TnVZbv02dssq4lwWyivQ8zw2fWxAx0tzoV+U2QS4oIUnz721+iB/8i52qUataJpVVy0TSavlyLIyL4QlJwi5fDLAiobclviwy6e6vX+cSItNnUQ/ppJVzyhas+zvUvb57nSuiHmaSnab913YryLybK+Qa2E70fJvqJPn//H4cP3abn6J6ivIiDiTjXKaZy3/jv9y446nrvKXdlDVXkHHuYZFxoNWb7T3taSLFdd2bDaD2B9X4qzTr3rHLeL+bHFUh0LxWy2QSiXxeRVnxSSVCQlWXiZOslIuIa9XNlYVrtGDozONlPtnayarehrC689h4bRQVPkniVRGEfScMcJQXIekh12Sgq3Jx11mANSu/ogknXiA0x/b6qrcpHpU4OaWoksT3//xjSyJGnPMsTcgZxpHfzVgeueFEUdBntFsndt8rpA/9ds9ImzpdKRodh+4Ustj+5FeHS+/uc1DVmZLI/VuLPLfTon77MzaLHnD8757O8ncIY05tP238cWytC8vS0keRBfqeXRU1Wvjq/F9HuPg+fmzl1GpXXQz/VWQW3fUTeVOjtPDcsYcEv189a6xAiaxaKpZXVnXrqtrLSlrY8KbRSIVsYOlxs15mEK19/+vajzf8P3vXHddU0rUvqRASOknooRdDR5EuKioiYsOuYO+94K7dta29966rYsMGVhQVFQsdpPcOoYSE9IQvDUg3uPruvu+X5+cfklvmzDnPeWbu3LkzOEd9WawxcB8Tzv5j1DzS/i3rluG1wIp5q9CZMhhILz128q3J5MtOYjFRRvTo2TKiqcg2cu6VNV9xf14RvAEBKJXvEwg6EWbcZyulNVaWvrGbXsqXrO+ovQikEoor1yYBUy3PH0yt6hisz/yW3Oozip/yjKqC8g694PkugqllbBKhiaKBtdKCyKG9BEQIDPx6qVSYCFLU4t38YwPMwQEtGJmsfHn0IHjcO34jAjDrHz4rgeCirQTeIxclVME8oyyEbpfNc0ry1RMvcQuOOAgTI//9x1odfztNabeIV1NhaouBVp1cA9hHjhqOFvQbGDUlNXRtF5xgiVE5DaKE8coFTgBFvRMWoaKSCELjDXt6J+5ewgmItPrMrwyLTTi+8xC288fi4xMTUwPC9XKvLf/seGTLKP4YDjn1Q4W64xRXBO/bz5t38yAaIAdvu66hC2Ztfl4D3H6Gb1fPnVJ0O40ICyQB9iP+CFb46RGHknprx9qmkbdXDDDpqQK1shzAu/WF8K4E6XsMwnd3TQpuRZ1qnLdt5dheLG7KrC+v7gAbOunLew0Etezrh7v4OYfItMlJpITMduc5g5L7qZBuHu3Wnb70mvfVbA2HEcv68tOBVBhfqxPiwZsfRKzKKGAbzhX5joBSX9wAM3Hhz/AllmZUqrufmOKN5V+W+rFG372fjM+SIJjJG85oGG6acmKhZ/mOD6sDJNd9oZQ9KWTaz7Dt/tyfQcj/0gL3CvWz7HIGvfLJ/gLczg2CTjwl5fbNVA52F38REVJ+/J02q71uwh5ga9bdC3UgvKORYBpCObetsYgWCpBkQaJHqYWZlUzDcJG1WejlxS3qxtb8QYWO7IwGTfeV67z5H9aRCh7XaAUvNlVXaBjAIuZVUrEBxjJnj0vX8Tts7Ch906A+YOXUUL4JLYUfirU8DvB1VtqBYuTnJndRTj2y/+Hxbnq8W5GzvtZpuq1Z5cHvnrfmPmkwDHXjZTOp+PUrInQMGfAcMTtSDru/cw7U0NvJAHhWXUPjAMKjlIyktCZoYBtgP2dWcE8zQ6+6m1hjOtIZI0EGcsGjCpj3ZBsUT1oSj+SBkSDzUDtBV1OauvVv8xmO0fzv3ahVb6rYpiNF3mHT6zNaYdbWBlwfNSrJVaV9pSA1FBBSjve4OlZB1guwUmKuGQQTcu003HTztlWLZuduP3EmQF0Rb4kKnCmDgbSqNzdq0PPx4r02ZURPdjQV5BTlS3xSo9XCIKGTSO/uxpeCrPoZqXODrKzGytI3co4CySIqVHvRKksmFL80oyG+2M2fS5uZJh9e0qbMtuUzjVKQ06TjGuAsnP3WmpxUjvSY5K0ph/aSfhMhMPDLpRJQKNpS1DLoJFbkU/VGGQneOlVeis13mrPBUPDU9+3WvkIObq6ZoHNJLk9JY5pv7polJZvnlPzzSW34Ba5oYcwzj8bXga2cLKVpL1FNhaktClZrUTrVamawKbzLF7ef12D913gIr5TZIEoYr1zghFDUWNPKChoBHbyFjKzmNBem1uh5OgvHIdTx4bNmFD558PC+oZHPlWMuFoJpvJSK50VMx2gHHYCW++RehZNpa4L+MGeDrjIpOemNaL9lgT2q31xEhjv7DggyVji3nkNJv7NrffPwv5b6iY9IavSN3pkodTap8M7Ms4QZG5eFGyjfNQF4b2QKCYCum4IJtOqmnr6o+I/lBdQU4+WrjHh3Zza+z24z9rE37OI9u730c6vW2JgAC37hpJLkNIjzUv7n0J1MOguAakC6Q9T+4WUuzHtdEK8HSPn2tVI36PdRgjUcyMVxBWDf0dayv5mEGY1ecvSr6Ubfw+evTeq/xlxsTjujMfs90SDMrmdRWVJZWpWu/xHXbr9zCHkfizU8BXOfKcWPjubTAKSrpwGU94a1orgZjjMRzKpmlF24/qUJQPcTfAHHaU9LJWC9rAUaKFmQ2NFOBp2tBoX3rLXbnnM9Fxoa48Z7hKWUv6hEjf0twJxfV2Lxu1QwfpEVQqFhvO9IM5tBJhayO49SdfwOG0nlX/JRQZf8he7OfFsAwY8WaKKUAyXIT8n6Umc6bOVQPQHnSx+XaU3a7GvMP7sl702upsdO/vAOhVDdBrcKD3Kzks9uhedwWjJjr+iMHg69fCy5fuxIY+HM0WoywspvrJuxGDcYTTnNndr6SAnGkyu+ZDBxm7hP1LSyi/cavE1IF/S9/QQ+kKIup70wkaA32Ipfz04mlQ3AYD1kbcl5wX3gOu+m1RuuKusr+amhiJByvMeoLG4GG+KwkvMfZANuFHjwyDnbTQuWXHi+tn+4At4qcqYsBtKaSus7NY0kYqKM6MmOpvycYhO/lbQjcIaCloteFr/nCxEwdOQ1+B3KaSwf0vqmSLK+o/YitZFSJD7gNp543YTc3AJ6gknkKSMhu1OqObbTcIJZtTRuRfJMVhzxwYA6XsikvTjECCzAL5RK4LuJIE6tycYNJXUg7tMv/+M14reEGo2BgneqtOKzdwsoADLQTvAlKrMqO5tg4OvZZZdMnrOJ5Znt8D7Cj20YufE3nhMBU0dT6e8ZJaupKLXFQK7MqtFz9xFO12FVvD59lOR3NArfPedZRoMoabwcvZINBe01i5hbSgb0rU1lyD8lL7WSqTeC+vHWBeMRM20hefcPHKj0f7hi8gARyrFJZaktIAMN8se4GzchETEah3dBLPt1phxMMJsz3AZJrX5bCekfIdKDhiKxcPrnzyVEPzdtbj+54NmJLMzsMR5iTwzcrsntrTMznNaPhmV//ZjOZrPYLGLZm8e6c66PlJ6hwiEX3p78Z7r3tNHqpV8Tirgns5nk0rsf9bZvHGkFoX97cGBVmumm1dNkrPPLai+oIgN6VqYKRE3dPBBN+ePRXfTwxf2Ew2lV7+sBM1sMhJB69EVH+LhA3eqsSoTrZuG6JLS8lEwyLlo38+55g9AonKcT5HpqHW2yDn/Upejelpw++47153WfGfVvc9ne8+0Fa053lCe/pVluRqUfeoSeEe7Q4zFSxoajaSGLo4O01J0Gjx12556x1ONQR3VOOYB2x4BrU+/+1eG7LFCnKLMS6jTKrYcdnA4Sjd5WXtrBdmxK2nCX6o9Ri2M5aGTfO6s9cAgYzKHUcQ8NQlA+3HtE9rRE5nKc1VKPPNSJGkBJrGJhwunxt+OtwsIsJAryqBE5OtTREwe9XlBGC+FPmaNlxF340Gfhu/68RxB6fWYK2+lPe4GLqN/eZ3ZwXZR+6yx6aJBcw0JmYQlFJChGrfzSX3Xe40IdxVhKlaqjYjaaV2TmspwWeApNKH+YSeszA5V0+5FZaLi1pANRYuQ3rUwshQeOEz6fUSo+fQDcTtkI2EDJfp/PsVkC+3LrnNGIcSg9DXresxJyONcsDin1eVwyesRi8XWH4bLOWWhHTm3QcgRerXyktXr1kLr6W0Ou3EjqO6zwSdXgqX66enBK3ucssl8Q74qCq3FZ5iPGBGsgjTTZX3KqyIN1kDw9+nQ0vnn45KGa5QX1IG0kOff4jURYxGTk4WswnGNnyq2LZiNmYKSoW5FawNKbQ/94KN549lCLQTjInsJaSogOr260ouMXc/ovPDacG0AlucpzrLK+ipafGjT5hIzQl+lhoKaaBNNTy3tyLcExMsqo7tTBY69Mos9MweuI50pbxtnl6X0PRLnpqeMmj/E+HGeAAmnI5y27RYEzbdSkGQhF6mux8z9UUSbxXMis+nz3fHP/df5KiB5EZjSHyLeNDgVz2utqiWxPFCX72GPqICuND2wrUOqdM3A9DJz+RXFx3ZDSN6T8uHxH7RUpkpFAYjXNXc0pl8/e05m5yBEpFKaKTy1IvCmK/x6k5OiRZ2Zzd8XwXqQxZNNe/G0NSZTAgR27f61UhsyyaZKXCKPN3m2WpBa3k1HVCtVTq0jYneK0uA+pg9GWV9fBtmi6fe5OhzNa7R3TC551/JHOlDCzwux6AG1rDiYk3n3e7hsZLEslFphCIBxKWW0H2xPRnnPvLNUTr5HDtlJ7eechetiIfiLDFJLV9JWf2mJgVOWXknX9+Y/rnLacv6IuM1ft2jQJLdLqSjeIAE3c+FBlAtfNe1k/8l5HvP7z+v3jpVw+vtl9psUlYNx8vMjMU3ZHcWU7o+T6iaHbjvNH4OyHzZrycnNw5LtRkdPWjx/oJVi+DKyhB2U83blBa+m2c2FmhLh2OqNs16MBsct5ZGUTiz4QsdHWIgPzKJdVoywDb6wJaAxyhVA6LYfvmCqRNqyqxO2DTnxsBT5GfhD93Wr3FRnvbFiNL6etOP6YDDzeLHa289yrvBnqHNKXV8+fZlgNminZO2HUvdt/88GJYq6776841Dw2cuoUmV8sg9SxBhBCO36+d9daf2wWnc1+d3BRcL8Ru5dNwEFZZZVVDPNwV+HIJCknq55cdPPYoE3HfRAQ0LDjUUnjD52wjwrAtqRdSWycun3TDP6EJnZrzhMCerqwb8xuLMiqopXsuhUUu9ZffD1mVkP6pbBlZVF9DehNRMt5qyKlvm1nMRksdtaixcuGhs07MoE3ez8jh4gLtRa5D8TU1ceWcn3c+JFm9qEntk2mbrvELrl/vHH7GW8duFZoEPjg/EULblqZBY5bEN342xZG6Z93Bl1b3h9Jepjfzsq8Hjd964oxCKBJvCAw4ZPIUQgwdMWmpM1LTppv9NerT3t2s3FI3Mbhlvy6NuSk1KCHCQdv2a1fsxo7Sq4dDNp6zl8b2inPMFRnA5nC7nhxO3n65nmOEsFhE6XqqJCN7IYPnwhmQ62EL7fbCt410bKu3Rq7JSYCCTRLOrBBlPysquykNvQy4XdDzPKvKc24KLygLkzC14K29qorx/23nAxAII0nLrRcvGft4sogaxgF6BM653epLRF0nKXP0fx2bpHPVaKt19jTG6Px6mCbiWNdnl8IWdRy+tAmOxgcM2EUfsmN4UsaxlpDSZ24GXOm8VPdbv6YPhfOxAQ3B7rAyCSk1+rZIx3hnbUaWnDG56iNmoe3xswyaztOYlLLrp0J3nqM20Vok6Auu7KmoplV8uf9obeXB3Ef26cvj76z5fAas6hRes2vniVWDdlxPZT3fkNprgIsgrK+UpAaGA+5hLTgyPIwu45IZxO/3HowdMsuHJz78Bv7/HOSlee2iZK9k05W6+tLa4NLh4UYMmuIRrtXBhuDFfAWgChwpowsAzTtIhb3Sfht3bK6QGs4maLrOfGPkTh1kMH3RA8ANGRGEyTfNr2Bw9wgh/b5LUx0NnVdtiC06veLtNLrhwdtPBaG6fPd4rohpW8QI7lxUaz2YjSQSKie0vSNIcQW/KhhXWpKqc4uYbYzUr8m0YjPEj/TR+y6ESIYykf5y6a9KNhEUQKzv/5iqUR1Nr2Wlwha+Q+lqMUu76AzO74cTB56cy4OyaaGmZ78c1Mk2tA+euW2tfRtWzklJ+Ma767hdjbbGUw2M+tAwLJ+s+YtX2UEBaNk8BzG9Ih2Ay/av9An0crOddye0MaIS4zs63cmblg+XPwNimQ1wXJTWxzU4rxGasXT/TeJ2sSaUhJ67YE/h0tMeZZuEAG2uPE65O8Hrsfbsn+GmwRvWsP9J+cqsP6YVQfd9PD9eRPNmLVfbm9/1WQycWeiZtmV64f73jw/ZsHWC2MdtA0Gx8U6t6mjjfkrz2gMXPvSUdfPCSOc7Y0d/vSSD8xQ1DKk39zTpf6pn1vU7fEuLnrSS6tCzEJ2toTIsUr6bPSQuPghcg+DDKZuv+rWqtXHXPIIzCjgtxXcf98rgE2uYfT5Y1W4XbelOn4XDu/KBtkM7Kqm5ehT9cM5wjV1QHoRaw45Ip28sYLxN0Tf6QezBma/KmxRMxt+fp9Z91JJYMywB+f7wYXOAZsNWP3UVscfbyw5wwnldfrq7bkZeZWAoYeLo6Ws98iGfute7ywF23p4C2cFYmfsvRwGFfM7wnF28lm3D2S0v4uVPoRDXHHoA9zB24hvpGnEo0uWiWWAg6uzPQrMaln58oSeXx9+7WBBpw7YYvB9BPNSJQvSFzvKLWP9gUsTclJTm9Xsh8c8M0N219V82K70flBTYV3Rkav2uuu6+Brxp1opMMxw4PlDfYzx9hhpmoBl1BGsiI2YqJ3nh3adDzYccGqvLdoZL9hQWsqBouQHAOOIZxcHIYVv16H24w7njEQYCIqEGk1dszfA0M1H8PUK0nnXqdhRqXn16ua+LtYyzJZzDn7CzkRXZh83O8Gf6tZTnpxwrjNy8eQniLbzvE83AxLzWhDm+ADr7s834c5TDpV4pL5vBJnbufQ1EjLDeNCOMjwZgTbgP43CJqw52E8PL6yXFHWNA1e/tNEVxprLNcfpLy8OfJ9WUK9mPiNmv11XAJXlKu+jHaV9JT81YAoICcjyMNhw/NrD/Q3wAncBBkPirtg2aOHspfyv67U673b4m7wGwMAuwNFYKOnyeavImbIYCMCt1x28OTAtu0oN4+nigBPG5LuiJzea8m2D2kTszrFKzQUsAvHmOmBWw4qDH/WFjFWiuC5I65sCyVKo9qKQSqju0ppoTrNPjTDr4jCbUFrYih25x47TDndavjYcI9JgyqG9KMDiBP71UqkgEWRRyzQ45rWTga8933io4/bj54JySGbOrnhtCIe88tVxuJeTINI6I9cdflgCdvNwEmqpTCWBms7fdRmfVgaYu/qZ8xLjxAErbLf8KvS/vNQWh/bo3U/a24kkjrqBDlL2Kn0yCCNpvBKB68YPbroAQTt4CjbbIeecHnqEdeTE0mDe2z3fgQERS+5uCzmx45jX+fWWMISeUferMYiuwyBd0ZvA9LEYyRuD1C3wfhY/ZlTvAUaZuv743o3shtSEnIDF+8Qm0sPM8H5mYqeB4D1L4YH1bTx8JE1wizCVvjkMbdSzWj5E32mozG8MeA7D9O2P6avATBjG10/Mz3BtrJnkSRBDu/4RXbfUxrmJGAlCmrhFmHSdp+c4SK/7Il0vT5GIShQkcZQLMMLGNcBGhoW6liJ1xXI7b8oYBtFxd5e72aqsOoIUsBGua9zDOoi+dz8Rd0s6sIf8/EppYI00RP7SEfkLaoz3Nha1QB3r4/edLZqkzwGjLAeKBRhq3MdT5LYgBBYfLuOucGNH30hHybtjjLrbC/GKSFFXKmG5ATQN9Jcmq7Jc7ZWv5KeGfELK9jCXQu6GIrfVMbWRwxsQAu0YinaU/FkebxU5UyYDub8a9PMJ7id1HyVET1Y0FdmGsHYNsO6yDePo2cNgZTVWpr4BCuKiUO1FIKVI/NJaXj4pG714oWNPadSinAaE7czwQF9Z8ZJH+x5I2PDrpVJBIsigFkTHboCO2J+h/l1nI3GBeBEz0M7hotySoyQghEmgf09i9PXUA2RClv/lpLZEAVCUjoH8BlM2YaSM/37guvB3t4Ri1eZ8LUOMtenuioKQ7oOG9rt530DRGt3/1eDQ2ol0DfW6pNMbCzwPz8f1ZuMAFVRQQYV/M/6z+sahtxCZSPXm22fOpXou2yPasDFb0kuo5mEW/882Vf6vw68jzN/tnUBwgRPCH52ZeIi2arCbPYrdUJbx8F2O06Lfoo3+LXth/mTQS7bPn7WjGRM4YtGV+QHyl4pTQQUVVPhvw39W32glV7xnX63DuM5etH6Pv9gHPrS6tCe1gAa1Mr0c5mRuKGPZDhX+DfiFhPnb94IZh9645JOTlfapNPMVGGVq7rtl40QdedNc/gcAt91y+tYslq6FrsKtulRQQQUV/uvwn9U3ddsZn2PDmLpYtGRpbAodvWj9Nk0NUHMrmWFm2MtNcVX4T+EXEuan9HSgOnjPgXjP75/4vwEICmv5T9ugggoqqPAr8J/VN4gu1ljW72A9W99xtv85O1T4YfwywqheTKigggoqqKCCCv8u/NreCaOxoriQZdzfWudXlcOh1ZYXV2lY9xV8gNr76ymE8sxGdRcHGR9A/iT8B4r4qWC2F5dU0owc8do/5f3cv6L6HBrhW3GjprWD5Y/R5L8I/PDRjR37aP1nX6/+3Uz8/4Nfr4r/ryBB+H+K/38LzJbqkgKmcT9L5Y1WikWM9uqsSoalo5X+r3LGL5X3X5cfrIYH53bOu5FOCfizcruP3E8//w4oRccO7Vz7rMQs+mLWDOveTxWmZNw7GH3yWSY6OuviTGflFrr+9xXxM8FoeLdp9/4/0xjj99yK9f77k+X/VvU5DEo7nd39pxpEHaUB/YEUIBfdXbTr5JUS9OYLl7ZY/9wYsGkUCk1ooxoMgUQIVIBNJ1EYgp/BcE2U7MUBfj4Y9Um/79y3P7Nz6oHYq56i4WOSSTQWz0YoEqkuK+mZJBKvHmAYAgXvvZL93Uz8EXBYdEYnRB0KBtgMGgusLjCbTSMzwRow7o+sTrDI6tz/EvwHVPH/EyQIL5///2Iw6++e3TEvNrMz5GDpBk/t71+gJIuYle/OzzxwPZER/CR267Bf4oxf3br9ut4JBBMRNSfxxZIkvOmvognCduG8ibdeHtCzQ8sQRGrBnt1XOsb9ttVZXvkIt1HzVr1+uRBlr2i5egDoKLg+4yp12bpZfr2uibJF/EsAwwSsn/7+YmbJAAuN75/9ffyd6rObchL2Pkw4/rqYYdRvoos2s7UqrYzhMnLJySmecle3lAWk7ejdE17fOKjlif7ZMWA2PL1zece1J1/pmJHjxs6bMHY4mrcOEb3x88m4xOtxr6ocIrYtmLvACZJ+fdcOWiQ3hZVSnx8FDDtgc1Ty5TVVQWbi4aNU3Ln7+GHig7hK891XzsVYSKzBxa59ucHhj4+6/pPWjhs/z12/16qgOBMBaurPrz6bkJuwN/b6vvcNWviwVaMnrR3MW2KbXp9y9Pbjg3EZxsMWXlo2xu37m8n8Z9FbVfy+iP3342/UUYLwcvn/r4NIRkCxY6OjHzxdXeimdEOpFIug5gHTN3xIeFvi7virnPGrW7dfObbIodRmEDVdbHR/XSGU6uziTuwKM1k79bEoBAqgr/hBkFbzvroTN95M8YRwBoVIArQQSraILFJ5HcXABCNca1K5Iv41YDUWF7Tqubn/8Gudn1Z9MMZj3B5zRPLr3ZRRyy5PNIMAHGLWSc8lMZP1rz0LwyomFYtUV0rRtsEI1uGhFWfXcLC+dkrsUts7QI1HTV9pRs3wumkwZtL44QbCR3W4UcDqCYx379kbt64Yy9vxjkQiUgAteG9s/jEwawoK2/T7uUiMECNsoqOXh5qUPNyeGZfZvNoCK75N7re9Zz+SANNVM2ct+tGxJUWZyK2ZEtXvJcBo19F7rXHt05ddVXefHSzcrBNu4j/Z7nncyB3xK7wN/20DJ3z0ThWVEbG/jZ9BvN6VJyYRf6uOEoSXw/9/HcQygtFUkEbWH2rdC81VikWs1owCEtbNVmrJ/u+b11ZX165tYi6DEeKHfm3r9it7J7SGgopO7ESTX9eNZRNK85s0rd1lrseMct+z1/071xNLv3JjbKt4PV1A133Bk+/cqQdtqQf8T1g8PRuNh/WiiH8NqAVZDXBLN9sfDdrPrT61vqgGQHhbCN6tgrRtA4cZxJ5/W0QKw8pbiJIP0suDi1ab70uNtoLzjcguaNO2tsMqXLb7RwG3cXfUuf71VSUtyqD7UZ1Z9PJB8+ClYYLNeAHUgAX7BnznPuI2/yAoeRn1cCsXGxmdBErxN6I+GMhIyiWMwGJ6ZIdZ/PxmpqkhUI8y1/5hOVCYiUpV/4eAxK8Yb3fuZOxf1cFr+ANC7ObkrYlm+7b0/Xd2TYDeqqISIva38VOI1wtISMTfq6ME4RXw/18FsYwgVaSXQ638TXphtFIsola+a4D1cTXtddeBlLpw8XGHvec2WUnJtvihX9y6KSdHHHp7AxWG0RFb/5VFaaklgQwMdWR1uZkkEpNUU9SkZdtHvEfIojQ3MpFY7Z/ybTS1KLu202iEsCllkuo7oOgeI5mtLTSEHko85Ti09hYSTE+w0TS5Oqu002iWqfD61uYOuK6s6jBJDTQ4BtUTAjaFUENFmOhLj6eQvzzPALuM7l7zUJkiJH3CojRRwPpa/D8lKyV2WWMH2IB3FZNIZCK1ucZwaMQ2pqYeSmZYlbkto/FzKc0izBLFd1VjMwWprye0lk1rpYC0vzOH4mdUXwQd9SX1gKFn93rhbFoLDdDUQkB4/yWRQJo6Ms0h519LBwWMwgpDT61Oru20DBOOgjJIzUSorqG6pBENzSSQtqHY78oFAonztAdefcltZHh01ZucczTJcM0Oq269YZBaOuB6usLDLFJrB1Rbm3svBpnI0NDm7WshYbPiUHaBQyc1dQDa2ih14f7kNe/LmZZjLKW3Tec+82RUYOaH0bclJn3tGBTWtR41h/h1X7JptF3Z6xx9Q1lJKVmEyIGWVqq6MJqKM1Gy+uQ2CkRLi3+415QQB9QuZErYpc1H4vIXLHdGsgkPL76wnL0+ECW+7ZkMpfpOpkhllgzIUkUWuaW5BaRtKjNhf0QVpUSMTakjUFEG+rL3QhEaJhkyDp3YxNbEIGTVVpJ4iioiEkcOhdhKR+jrCrujjJZmKkJXW6raHBqpjQhoGvTMZpKUCGWEWrRurW0dgKa2ruB+EoQX/1ORREhB+Wj2wglscmUTYIJF0Nua2sB6xiiorJvQSnLKGUZj+ki8hWRR6tuYOnrSLpXLIgnQG/NyaJhZlrz7cmitdRQNI73umyniPzH/eRLIdSFWRpdD4tAPyfv3078L3+ud0Oo+nn2amZn96lJqx8T98de8+D/WJm2/9JGEtTBXq3zwlhCyYvN6F6EecCjlsVevxjVAtOHED68y6JZDurqxnI7y13viS8BIyus7T6ljDiXOcJDTp2M35z5ad+r6E2j0x73DzcAAvfSK9/yHXruvnPNAAKyaI4tnH7TckRXjgWISUospaBcrfTA17+nRKYcep1NxWy+c3WQNp1Unxuzcf6Qm4NWN34KFUaeXfXx8Jas4+dWTlx2DXtzcOBjJrC0sbtdxddYCd5Q/Xb794Lkiap8ZF79GW4t0YunFr05N33+3xP9Q8W8eKN6OrBnHbzxPrSt/8TbfYtHFN+MtumPYURi77PKbhORmut2VqVsspsxfEIntVFiElE+izEufnphz/GGa7da6Q/0bhZWy3Hbh7EaxIXd2c1bs7O2nHurGlO8xv7w5ZmOR95OzY76d3vVbEmPRyWsHnHi3p5dcCd5et/VITIgmJVup23KfPSo/NKP6OaDKXp3d+SKvpCI7TX3M08Pz/IHczatXbM83XHr4zGE3rhtoX07NCnjp8uRKTJd7f0b1JSlBqyppYKlb4fUFWc2q+hj3pMN0VoQ9O/ucz8orXwzHJp1eFsQzJy9m9uLrznu/xTgWxx7Z9jblfgvD8+r2CRYhe+YHGxEKMim6AVZaYGr5laN/LIovIuNmZp6JdhHIIb327tVL8RSMA1qt4P3bWq+V16e56AJKewwAwFq2QVjgUHpp2zQcf0MJVtnrWwX+c/cLBk7o1bGndyy4WxNx8OZFDwSbmLV/zx/r3uudu7XH4emmsPNFofvurikVs3nXJIP7R+SEUtir4JBKnu+8k1pNb09/+zFXe+Tbq6sDENxfyz+0aHk7yJo4Qi3/wHZcHIw99/BtXAklTDgjg5794B5txHLzz08BpIH4MLHsIgQeS3j87G1xVuzT1PaBB0o3emnLz0Tx6quTSp6u2XvsdKHtrbjDw1uFlMDPvPg1SjCXVnmVEAKk770u1NDvyfUn07f5Zl2+ZTbzomOPzMtUqk5i9uED8twrI7Oex24OEX+9L0sV6aVvrmz7SLEwx6hVJd8jeJ3YNN2/q5P0Y6ooKWLs1jdx1/8qrPv25e0X7OLMI+MdJAeqZIUMTnx/Z//MM0m00afyFjvxXMMo2bH8j7IZR8/1haRLJYsFRHZFOKRvJw7tWvuyadju23eca4/v27rqdTXYa33xnhCt8vjF2w5fKWf2XfLXh3GmkK46Zz+/ejitkdJedO9juUH40fzVrmpSEhHOeqOEUAvuV3Lt6p3EJlpL0dvH5drzjlw75YqQILzIn5y27AtDZEuEh8ROMcpHU3knsJsy/4q7d+JxMmlozFK1zy8Li15nEDxm73841QEpLghco3NzWvQcHbtXWeVQy2/deJwFQpLT71ymj008OMNLQzGLZKO9MqcW5dgXVRd77upfeTV52YWao/e9nuemRZLPf0jhgSOX7qUk1zHtdmzf7BiyYE9w1zt0qvQh/V7Kux3nO+kvAUW9Ew4x78bsWOiGmPlLZszaVVnL4e/cw2p4HhXzyHPL3u08G9iR6OVO2y8MvrzMR4Pr56ytG4/UjPzj2jze9tMnij7ttLcQbFNOK78/bX/1gu2LQ7RJ+G+PxyVn1U1zsJFVOqsp7X6tkb8O+UItldXJ+wVugDOCwk0Ew84QbXsjDR0T/lAStSq5Xs1mskHJw9NnacEXNoNHrEuup7ABWtmdL+Age82zgLNwqgGH/PnGn/thURfmjd08c15BLQfHYzy1IKseZDrFuPbBukf08TGbIevWPWyhsESMoZS9eQ5289J8BLjwX60xyo/suAJZvueyKait+H2SmlgzoGk34ci0llcfO1Zu3LXaXKAc7QqKkPJJ5je3b+9RwSMN4+ttdUsenrpECeJX6l0VmXtFT6NIr377V619pL32ZwTiY+wzZvDia5NM2j819vUzBr/twBsKzqR/S0z4wgjBwDjNOU8Tlbgtr761OYWdxgNrnzzRH3Fm1xxI4+OAiYd2p48/QP6Mm7NqwrZdpy69W72f22VUt3ax0noFV1f7idWXpgS9opAAaPmokxpKm+pS3tze9pgwaePe7XbNN65hd64aOGnXg63vJr4YjgGrmwRYImLh3KckDfcJy9a3psV3jP9r5yTBPrQtVdnlaiYxBrWnTz+iBK+7CY4Z8b6ZJPiihtXw1661Z+22Jsy25ul/MGbg9D+2eF7axHmmpMd44JZuq7HnW3oRZSCaexdK7tFE/VXbLPj5Rst98wXiaq/1CPA3UwcY1fde1HoOcDDIQ6ByYq+wgg9smD7QVcOir4jNnbVx8XlyQikoj92cfmlhInbz0vVOGqRHv48bS+wj0IOO6swSNfOFsiZ/0Oq+Veo6OthCgpAPEj9WUtwcePVtfPNnrvv6iVrFT7jPo2i9HufLLYJD/rZ3Tyx8+rrdY2dsm1dZysHyJrrKy0Tx6nOIOVfSUJF+hhdabNG1D2KeUMfyKXG/kczkpnlvVEIECK/REzzvH9/+11W3dusta3oeLWQr1dnI+lfyMkVWZk3zCBTrmshURVbli51hj+xv7ZnjzCsq2Hz5tKkXvXKX4jWBH1VFSRFj5N3dsQO8POF3UxCp+GGGmpHkY7PMkDFKk19VO/hbgt62WxoKPEMrT7yYz5jCU1C4VLLIqchCbNK9N20mpgg1wFO77NCpV/CIzZdYK6IaqcSCOxse0CPX/U5fsyWdxPvEjmc+m5h0+cANzIzDv+M0Se8jIjc04024fANJSASt7NoTZYSae7/0bQdfWkQvvYzTaH3/m/lGog//PYgE4Xv+ZFTFfZEnET8azV44gVFTQnL0taH99bq5osF1w++LtJhZF2e5Xj6bELajzxcRQeDFo/pdjZrDKLOuvln5yR37iiJ2HOir3Wr57dymd8nN07xMIQpYJAe00tyqTmOPkqcpRmFrHs4GV8Uvtjr0V9J4NPBWLv8BuN3KZdMb0j4SJ2x6MNFcTOk0pA/1Tt5rRjJeKEx/KcjPfE7bp5Xbk1y3HXflddyghub8XS05zfcOH07x3H1BKAJgjIMbtjExsZ7pY068s2/bPcdtHwca8UxnNOW1ga2cjHlX00v27YxVjzo9SJtV9ur0lkq37etDreQUDTHsOyuE+j5HHVwPAfMbPxa5sYEBCP7Pe91At5oVbMrTsvq8PIZ+cMuj64aR+0easHKSAZhxPyN1QN1yagTq4hKimacDf7d2TtOnY9Pe2Nw5ZsPrYUB17AUbdNLrP1cwjNxbzr40WL4owpqd/QCAWTkaiQ6wISyHzEclBBLRg+21eHci5d/OKLUvJ7JN9XVsAkZJ2s5uzEut0XXzNex6qFFQhAyfDPfEo/qSP00gwC2Ad7dg4w6ONGPlfOB6xB0jFju4afBS46YLD9lovbwSrzmbPbQFD+npZ84wMIPc+ZZy2tMPPK7V6e9mCQehXMYsV+K23Itay77Vspk1WoMO+mB48dHQ1gUzmymddsNnOQBMn/E3Yy89T24bNkkf1MnuNPYKxIu99/yb1ZeiBIOQVc+EIKmv4+NeqSGMcZEJ11ys+KtpzJhpATDxK2++2voiu2kYBgvqZAEGIYFWvPiyWz+nNqFd8aZCK+gVeeU0fY/6Ry9MIhfNM2F/SAY0jB0tefzl1L89tDTX61GMtSDoYF2HAXqNN9Ma905X0mNCmuA9zYB331LbWH4IoCzxdnnwgoFaAuVQ7zMkQjdhMQHt5cX9BWYaOc64Jv4BU9f2c63njmhPfeFbM1GbjUeP1pcTSr5Xqh/PucxZszPMSYP3jqiskWnqZcnXKVZTcVGboa8zUlq0OC2l+WoOQzRRWmPx8Bsfv1TMdnCEUj7ceaI/flsfCOVDK0MNhe6eNCK3CE7b0+Pb79j8kWzD/0RCx9yBf77cTARAotUHwV0WRZKfbiFoYID7r+FLF0fYsbMfAxBTW0xvVUIUMNNBqzzOTH6cu+TSn/bdgipPqVoWbpDvXjmZJeJHWarIaX675HDu4N3rnIVF6Xq561UlppYz8X1AhB9URUkRI31JSs82KyOwTbEom1EBkk6QEzIYInC0ceGZ31mYCbbC2r6+9agE6RNkBJcinvyKLIgKi1rQ7/WK3Sijthcf7KYujsTSXjyGYTCEs0nm61cNsaGnXO7UsLIy4N+UWRy/Zxtn0oMwnCZ/ym0VEx2CE5BSXCKUFGpm9bm9l9gTd83E8erWWtfIMPTqw7ufBOFF/oRZKJKIH4tmL5wAs+rvr/s+oQJAjRwT4c9zPNzcAYdi1NRSIONFBYH3xrU4nWw4wkpQB3pW7I79sOhPntrMule/XaoMnL0+yhgCsOWzSB44pNxvBBaDoD9ocRiaxyqkNgrCJLYD2CiF8sJuzUsk6AZ19VxEIXmol/Juo4+yU5D+MiA3+enZ907EGU7OFt8Nmd30fn8KZNhB6+4Yd3LYnE4Og91Jzr2y5ivuzysOgicNSuX7BIJOhBlvjZaW1MtHCC4nNNMPn82uRvrcOu/n8J3p4Z1sJhsAQ6G8HgmrIuVFJgMUCeL9wX1AeKUbvpu3xSCHWJFT1UnOa3G5N8EEDrDrinJbsAF9Ba0CpfxltYb3TGP+uFXpsZNvTSZfdhL3N6ej4mNjZ1tFc8D2CdYw7vXFKe3YUQ5aEpaRyr8WaThtNeaHTtt9sS97yvq5bQu3nh+H15N8fCGnp1Sp20c5aHy/CHk+oTflZZLocLrH6hAzQaUI6H79daXeL9Kq3tXRiXq4iS5dAspu/ZTaqOviacOzlP7t0bkbRMgAb0tBpJS7La0ouwYwi1zQHwMRXlVSwtD2xwqiBbXxH4I/fyuxijZJn5WSTAob5SQ+RvoTqi8GekMGAcBFRm6aLWsIE2oyKsRy4+3UAtpgLCv3AclnIX/cGiAXJVTBPKMsNLuMyMtt5JAr6l22rzLhGZHxrd0iwJGnhuymh7EpUO9DLt3J0clhcXjc61Q+EDyADe1dzYDHr8qoS7WKj7wzW73FRIRrlG+p1UinWV1zDmmFWXVUsl6fQa763TWWsFlBKFkN14/egow97s2vK6M++UoJ2DHKGCEIX26Durm9mYweFC0/k2gzmPu8jOg/wAH6Z3ISYbI1M2Ff/eDDriiA2VDVAWhZawmvk18ErfTumreGay9JbEOqMBMlqs9o+lJMokLpAyeE2AkoQUQPceK5tfcq0Y1OJo0Jsh4UhhEZ/JGvVIozRUZm9UCmKrKr38c+gXgnWonQiN3J4bBYncDfUkVREQO0B4z2ZW9f35e86FbMOB+Jb1IUsYLdkPe1CuUymPdAx32ifbgxkQhz8+4jyCgx4imqCABQi7MqO+gGoIDJY7EQbichq5TYDqMNXzXYBgYwagtz6UazrQQMfbH8FnjpMYE4MMvfP80CW2wyFpYnIRFKCDWr8uXRg+Bx7wTZzax/+KwEgovmT+mSILwU/+VJxI9GU3kncINQVVDeoRc830U4B4ZEaKJoYK20uBQli2ZER3VuJczcS/Alfnvq9juEgJWaSXfOvG9CDt9yYaQFjxPkLLkskgtadXINYB85ajha+GFQTUkNXdsFx326U8j/tqKUQpj9RnMZHQaJQz8i7/LTXxbk9U7oVXcTa0xHOkssLEGuyihgG84VmV1MqS9ugJm4GLC+nExqtFoYpCvwGOnd3fhSkBX/+YmSkZTWBA1sA+znzAqW8VwnCywWBwBBeYspkXKOJ9RwAEMETI33mXj8R9uItfwvDujFOdVMmMPscX35RpLSUmoNvTwFTKPVZ35lWGzC8Slc9eZGDXo+XtIF1JrsIjas74jIIfxeRkvhxxIdr0GSU4Ho5Zn5NItoYTJDMJM3nNEw3DTlxELP8h0fVgeIja9Syp4UMu1n2Gp/vwi5PiGWZlSqu5+Y4s3/6JOU+rFG372frVR7wyDkf2mBe4X6WXZHkFzwqALmPdkGxWNi4pE8MBJkHmonbCKUui2rNaOIih8+0K6rb5yf9LxYz/+0nTClYUZ9w7EXnpURGSY5N+gh223F+ww/o/pidWwpL6aBTXH6ct6uQi37+uEufs4hMm1yEikhs93555HLU9KY5pttuloles37araGw4hlfflGkArja3VCPPhzAKlVb6rYpiNNehSLXp/RCrO25j0CNioXCAE0Td1c4bezsiuzG+OIw5Z6i2lg/dt8hmM0TmgQk/Alv0XDYXi4yCbekjbLDyW98sn+AtzODYIxXUrK7ZupHOwuweoOLGJeJRUbYCxjogaz8VOZujdv8hoI4xLo3Hnybk4FNu2D66SdOAhvRckqEqBlqCUc55VbBL3gTWIxOsJPMpMUZaJk9TtK3zSoD1g5NVRfQIkPxVoeB3gN54+oRFf5DWkNnfpeRqJXyVcqmOJMkZFZPQXJVEVqYWYl0zBcZLYavby4Rd3Y2hhG+RL/46ooKmJc6TEP2fgZjo7847jvnLK4E2tGiSz/qYgVADn1Q4W64xRXBO9725t38yAaIAdvO0HPWJx4CirCbV7b0nJadPovXenGdxS55EWdetDqiQN5ZbIbclMqDfsH8RpCRv6T2K+4uVeFtuQevFnIxs61F9giJRHfF2pG5aXYfKc5GwQfYZG+3dpXyMHNNeO10xKEl8F/2RLxo9FU3gm8qhbkNOm4BjgLpIDTmpxUjvSY5K0pkREsQkUFWS9AMH+eVPz6FRE6hgx4jpgd2dNVVcAiuWC1FqVTrWbyXzLwK1F5+3kN1n+NB9ceogL+U3I/FdLNo91kiIjkoR+Rd7npLxPyeieMppzmTm19pMTxTiadBUA1epZgbP/wMhfmvS5Ik3irpB2BMxS4lF4Wv+cLETB0tOXFhlZbTUZY+Y11M1Z6tR0Ok8FWg4JBAOXD7budg/sblVZoQtUoRXH7SUOOCR6k2e05ea36QTGjBbN2KCUPCiF+YwUh5zQXptboeTrzZ6XRmkrrOzWNJKvCbi7La9QKOh8gvD7rfSHMeayTRJeR056WSsB6Wet21xhmNHrJ0a+mG30Pn782qf8ac5Fp2I3Z74kGYXbdOzQrKEKeTyjfvlbqBv0+SvAUSC6OKwD7jraW9hupLK1K1/+Ia8/qVuSKLxlM3CZu95pWdvFeg7cJ6YK+t59wT3LlbkutfNekF4wXTqZh1b/67S5p5PIov+62Fm46CI+6kFOWSk+xHrcKJ+7Rn1F9cXMaCmsA3SCM3CRUN/X0RcV/LC+gphgvXyVo7ZlV2dkEA1/PLivY7aWfW7XGxgRY8A+TSpLTIM5LcfwwdzKpbAAmsqBoS86LFKj3eTct5QMhBMJqkCkQ//HhDjPHDZvE1hfgtBcmEvQGW3XNkKSUvm7UjVjmqt9ziqTN8kPJIeR9LNbwFKx9RCl+dDSfBiBdPQ34JGQ0ZDaDTCz0ZeQ6uSSZYfU7/4EbYug50pS16+pBitP4OHu+b5nESjKggxb0ThQUQaopa+Zo6kt+d6woEyWrTyr/ko8KuuQvdGvm2wIIfrTzD6pEF6i1GS0A1tJQNHflKpUWQM5RkCkyMqsHslWxk0HnihW8Zxnj9pzrudDQGDd9NvHbj6uimIjxAcMFLnlz1nTcwkObnk8ePql7WoBCVlAqnhcxHaMddABa7pN7FU6mrQn6w5wNZCWL/Irw7sNtiQ2jV/QTfItOKv2QozX4pq+A6qTPb8u13efaw3njaJ9SapAegljQMh/d/UoDdF3tjQUMlZSI7ws1h/gtoUZjoOBlAq347N0CCoAMtDPgv+AQJ7ws/suSiB+NpvJO4Ic3pZpjOw0nGF2mcUOfZ7LiiA/3QvGMYFQWN4MNcYKHYgqhug1uFR7kZiX6eKOIRXJBrsyq0XP36dLyitenj5L8jkbhUYpbCmbj++w2Yx97Q+nRDMlDPyLv8tNfJuT1TiBII032l5wq8mAdJI9Vn47GNw+fPNwW5+kEuZ5aR5usw9M1StG9LTl99h3rbwhqgYI57XW1RLYnipJ97DF1kJXGB7YVKPXOGV1/Iz04Je9zFtkvCAlwSAVX47LMR4wJ1mMXPju7K0cvaub4AZJPY51sNofdUff2zoFzjFEn3V/e4NCq8hKWPqibsn6CcCUDanVyAyIw2kmwji+l4uNbKm4zKvNovEF0mEleaiVTbwT1460LxiMmIPW12PkfqiiTdHiPD1Wf755v7r8u1KAoqwHlOqOfkD7lCZlUp2jU27uPjUNHeHb7i1KRWMXChNPjb8dbBZncOZcWsjg6SEvdafDYYXfuGYuPxHZU55QDaHcMuDb17l8dvssCUfKLCNKV6RNk/dtctvd8e0GlOsqT39IsN6PSDz1Czwh3ENFLalFmJdRplFtP8Nkt5QX1IG0kOff4jURYxGTk4WswnGNnyq2LZiNmmCt1W94XaFTdCDR/RgYpZ/fOy/QJu68PEhkuB9QdXDGky4+P6g4/4CjJqZ9QfbFXZazmyso2QM9ZxgvQbnPMA9GUPx7dRQ9f3E9oDq0wux5A25qDCYl3n7f7Rg6szapEuG52FBqRl5JJxkXrZt49bxA6y9piEA6yp7CWEqLDby+Kjl/M6b/w2HDukxBDyUB0AaLXF6/f+eAzaulivLi9pIrUApbeHPrHQ/HGs8Ns1aoz8yF9FtiIpq2EzWM85YYy1I9Eo7eVl3awHZuSNtyl+mPU4lgOGtn3zmqHzMISikhQjFr5pb/qvMeFOoqINLkyrVzHVTgtHmY8rD96yz3GuD/6C0SW0VZTzwb0hDLN6ZBbRICDviYrP6eQMtiQl0kNz+7G1/WfEm2gIBPtOWLVt6jIzGU5LfAURINa/jCT1mcGKun2I7PQAbIpoVl16uCxVybRZ6bg5c0BpDQUlrPhziZivSakXKViVyrIFBs1qcwSjbJMVRzi6ImDXi8oo4Xw553SMuIufOiz8F1/rr303qtidwpQRERsgPWbc6+9Fm9y00LgBi/pd/uYgehHzgpCFhKtX5baAjLQIH+Mu3ETEhGjcXgXxLJfZ8rBBLM5wzESxHOTWxGgozI1G+4q7NYDtPxPOYDbKldB0lFKHuZzXBdDn916ZBXq1kpjNFVwq2xRnXT2CM3FXO0dwx6eHPfIYHCYnZREfFeoV+NJHYy2vLoOtkXT7XN3OpzRau+YXvCs4490pviIE54mi/8yJOKHo6m0E0aEu1IrPrUg8aYoXphoJUePPDObuyuG/ypFXBD0a6pJMD21vCfXEhwjI1B6GvS8ZyXkcDceJ1KfxyWjRyx2Bcln0bBpyPcbr+Vgh81c4S7aiDKq8kvJuv78NQo5bTl/RV1mrtq1aRJvXEdhS4Gpel8PmNliIITUoy86wscF4rqfvmkShzxKei3vbPnpH+4lI+Pk9U407OaP6XPhTExwc6ALjExCeq2ePZIXb6Nhx6OSxh86YR8VgG1Ju5LYOHX7phlG3BroDRzmBjm0z29horOp67IFoVW/X6SVXj88aOOx/lj2hFH4JTeGL2kYaw0ldeJmzJnGT0Jy0ZfESy8Inwx90qdLvMkG1LheLDq9CLvy5QZPvYJXoM6Kbbtf7jqwa0RX9rJIFQUs87k2XQNnpdnl1MJ99wb9tcIHxW4qrmxnlFw/MXTbcVuEJj1icZ+E39Ytqwu0hpMpup4T/xiJU2fV5lex7MOtBW8FOaSy5Hpq+s17EzeuDBMhMbujOr+dlXk9bvrWFWM0vh1PvxS2rCyqrwG9iWg5b1Wk+CJ8LCaDxc5atHjZ0LB5RyYYwRQVgSDJ8gm7IecJAT1d2HNmNxZkVdFKdt0Kil3rL9YisokZOURcqLXojxANLTjjc9RGzcNbY2aZtR0nMall184Ebz1mg1DytuSavCpGxeXYmwQksaSWZDbpYLyPxOghSFNPH0ok+UZ4Y6U613+/+j33Ytbdj71x6n4xV11OHDtUFxT5W4i5jCEUkDrWAEJox8/37h7mZjOYbGbWgYBl/WbN4z4sqVWmVDHMw4UKwu1zZdWTi24eG7TpuA8CACGmL4++s+XwGrOoUXrNr54lVg3ZcT2UP4LbqlwgeqBh52FjUTNgg6vE54psYk1FM6vkz/tDby/npiq7ojinGRvqIjZwKmEztEFuKFFqTB9byvVx40ea2Yee2DaZuu0Su+T+8cbtZ7xRnQ1kCrvjxe3k6ZvniXRNKBmPrh14/PJbXfWG87QFk0Z4ItXxwUNGw/rP4i1fRi94cW3v4/vfuI6+cWh12+iY0a6mrvKKMITCx/gknAlf3jzaGtpGQQ2eOHseDs6qk5+JALtStPrshg+fCGZDrYSv4tsK3jXRsq7dGrslJgKJlEkJDiEv9vnnJCvPbRNl9U6Y9Y/uxN1796gCoLdd3b+iJjxmrKfgUQ4iV6nYCjIFYNdLZ5ZokGWpIggYumJT0uYlJ803+uvVpz272TgkbuNwS56s/4AqdpOiQ0TENFLi0rbFLM0Z1teE0UQwmn9ygKj0QOSHDAVq0dCDMp7u3KC1dNu5MDNCXDudUbbr0YDY5dwOcps48dTBcivCqslOb0JHCsbauG5/8YnYZ7qVgOsMQkFqG6Xw6r1Rm1eNRoFYPqZrrm+yiEB7ha68PYk++RIn68G9qj/WhqJAzRISwW74rlAjGdQw05N/bopEG9pHr9y2lr5tK6fkZFzj3TX9UcR8UcKzW2TxX4ZE/HA0lXYCgtsbzi5htjNSvybRiM8SP9NH7LoRYqEuLQjsOiKdTfxy68HQLbtwcJjBxIWWi/esXVwZZA2jAH1C5/zuweUEUz6LkJRPn28+fVGTZzj83HSR+TrU4rxGasXT/TeJ2sSaUhJ67YE/hxsJnaKI/20sOpv97uCi4H4jdi+bgBP9ZJ0tfkitIb638s4myE9/mfkmd1Ys3HnKoRKP1PeNIHM7l75G3aMEiL7TD2YNzH5V2KJmNvz8PrOu9WCgNhG7c6xScwGLQLy5DpjVsOLgR318f8FkH+d5n24GJOa1IMzxAdbd68pph2248lp93u8IqFRLhwpcsOvBaL1AVwveIKDj9Fs7AlHOnq4iT0cQozEpcWEcmOBSENZ/zSsLpLeTYAKn/phVB930ukqHW687eHNgWnaVGsbTxQEnqArIeNHJ+7O6r9fzP3PQQsfJyUJ87RuwftCpA7YYfB/+TCuv01dvz83IqwQMPVwcLaWm7Bn6rXu9sxRs6+Et3GxEURHasnwCxgx7cL4fXDh2BjYbsPqprY4/Xmr7RzB2xt7LYVDR4Tew8aAdZXgyAm3A767DJqw52E8PL7REudvqB/7Z9qS9mcJBaOtoy95uj91GYPSftWqOmYwlQf9+9XsANRo1dSX3nywbRM0h1zD6/LEq3K7HHJ2R6w4/LAG7eTgJJsdZjj5VP5wD7zIiYs0hR6STN1YYZpTj9JcXB75PK6hXM58Rs9+ua4krZQMh6r1+KxJcDC0kEwpsHLj6pY2uXx/BCyqwRei+bB+oqRjjJW1WFErH2cln3T6Q0f4uVvoQDnHFoQ9wB28jfnUMB54/1McYb48RCw7CLXzuFe4/kZ808XPv4QX/hduHzDrH/Sd6hYIirKe+uuGRmN0IwtgHOAjneYAUZSIgXn1M1M7zQ7t4CzYccGqvLdoZL9g4WiYlQAZD4q7YNmjh7GUuQgvFhk9awP13UcYxeUqlMFNkZJYo5KgiwnH9gUsTclJTm9Xsh8c8M+teKe0HVLELYDERG7z6WkV4xudGwMTOpZ+RpPQgFITMYHBcrHObOtqYP9qiMXDtS0ddPydBOCSJJ78iEOuI/VmDNIwEBUPNlh26PA8h7MLBjIac3eti4oo359+k76wTaa7ZrWiXQCttCId84tAJDXsnnIChkhKhhFCrO24/fi4oh2Tm7Irn3W/lq+NwLye+C2BihAfL5L8MifjhaCrvBDahtLAVO3KPHacd7rR8bTimJ7oSgmA4fu3h/gZ4T8H3ckjnXadiR6Xm1aub+7pYd1VEEYuQPhtzD2l4n0WIL+SnPXr3k/Z2IomjbqCDFP+KWiH/dfwuHN6VDbIZ6CT1Ql3yUO/lHawo/WVB0Qd7cGNH30hH6d/BKFO3CFOpn0EIa9cA6677Yhw9MaLHsPhwrMQFnLaCl1fagncOMZK2QtPYfaRx1x8wjL8/RuoUAATriQhY2ya453kHgnbwRItVxaCfT3A/qevVRa539ZD1vATR9fLsWTMdpI7p2x/TV8Z5Qjt9/cTtVFSETJ/A0EY9P0H0nYbqAzIB18aaSfzENa5npEPCA0reFgRD6BjJf53Jbvl6sTTw4ELJga6uQv5+9XsFdkNqQk7A4n3in5XB0c7hYrEHwUVoom/j4SN+FzDCNNBfms3KBqKnGISxkyzXQXQdBomuug/TtkBLniNps6JQQgzt+kd0naeNc+upDkTH3f2n7HorvwhuY2HgFBbsJHGB/EyUrD5c19ii55i+dz9Rt8qkBFjH1OZHayVPqRS4V1ZmiUGOKoIRNq4BNtKn91oVuyFuGEjdzLG/mQw1Fp4sP2QghF5PTkuGQzJZ5FYErKGP65nXA9bUMegZ/oMa+PQzELFFx71/1xfPIKSjK77nkKREKCXUEB27UP/u++EC8T0HxAgvg/+yJUK0vF5FU2knUItyGhC2M8MDfaWpKx4CbuDcDUWOgtSxPn5SnJDPIg6p4Pqz1sg5cyUncYOgKB0DiYHc7jIUtBRmeD85/Jc61Ht5V5j+0viV++woBKf12+PjOfprfh/p+J/afEqFHwOH3k5gamg2v/7tfMGgpQsc/+Edgzi0diJdQ70u6fTGAs/D8+V0lVRQQYX/p/inJYLZkl5CNQ+z+NX7SnNI387F5RhNXD8P9z/ZiP5jvROQrtPIDZLPYCr8C0HPujrP/WqzhcuI/esXRBj8Y4zpMqdk+/xZO5oxgSMWXZkfYPxPm6OCCir8u/BPSwStLu1JLaBBrUwvhzmZGypcluRvAYRymjv9f7gRVYm7Ct8B3C36THkYC4PRlbmz2X8acNstp2/NYula6P6UjSRVUEGF/y38wxLBptDRi9Zv09QANbeSGWaGvd4iWAUhVL0TFb4LCMrC6J+2QQQQFNbyn7ZBBRVU+NfiH5UIsJ6t7zjbf6z4/yGoeicqqKCCCiqooMK/C6reiQoqqKCCCiqo8O+Cqnfyy0BvrcioYlk5WRuqnKyCCiqooIIKvYCq4fwlYFUln43ad+M1LSD+9o7hsr86V0EFFVRQQQUVZEJx74RasGf3lY5xv211/v6X2x0F12dcpS5bN8tPqa+8qanXd+2gRV6c6SxnafD/akDM/KN3pL4IzHC2kbETtQoqqKCCCiqooACKeycsCoEC6MN7lnVmkepKKdo2GBlrvzAoRBKghZCzBLT0rUlECqAFV2rshkUqr6MYmGB6t6/6zwSrra6uXdvEXPk1bziUkmKitpUNRjU6pYIKKqigggq9g+K2E+W+Z6+7yN+klwcXrTbflxptJb36nq77gifuUr/Kv/WABfsGKHdqW+oB/xMWT89G4/+pVUpJqQsXH3fYe26TldIWMBpS6ztxA01+9XKBKqigggoqqPA/h+882TNbW2gIPZSwL0LOv5YOChiFlb0wMJPUQINjUD3tN5tCqKEiTPRlj6cwSC0dcD1d4ekschsFoqXFX++L2drcAdfV6RqnIH95ngF2GS21VQKL1NzGQOrpd624w6K0EsHavD+Z5GamhrBYNrmyCTDBIuhtTW1gPWNUz2ZQss8XHmpuZCKx2sJbE/OfJ4FcF2KlLBA/radqFBKdUpPRpuVmqa3sWJIKKqigggoqqCCE/N4JrToxZuf+IzUBr278Foygpsce2fY25X4Lw/Pq9gkWIXvmB4tsx0ovfnVq+v67Jf6Hin/zQPE2oM84fuN5al35i7f5FosuvhlvIdaw06tjT+9YcLcm4uDNix7qpJKna/YeO11oeyvu8PDWp8u3HzxXRMXPvPg1yppVGLvs8puE5Ga63ZWpWyymzF8QiYUAHGre6+vnSsA61LTDT+lLDh7abMtIjv1z6un3mLW3EiyeRsacz/Den78A9jju3onHyaShMUvVPr8sLHqdQfCYvf/hVAckmyh9ftmmvtoAp6P89Z74EjCS8vrOU+qYQ4kTQaePXLqXklzHtNuxfbNjyII9wTwLJE+b4cBbEJBDyXt1Zce7BqgmvDnnVRLTcqqJ5EaPKqigggoqqKDC9yCvd0Iru/MFHGSveRZwtuO1sBruE5atb02L7xj/185JEruZU8rePAe7eWk+AlzMeI00o/zIjiuQ5Xsum4Lait8nqemLF0LLffMF4mqv9QjwN1PnEHOupKEi/QwvtNiiax/EPKGOjdkMWbfufiOZCQBIuwlHprW8+tixcuOu1eaCUunfHmyfXz0qblFffZJlyuON97PrJ9SlltoHe2nnoRC5+5+yxi/asN7DkVyS4ehrQ/vrdXNFg+uG3xdpMbMuznK9fDYhbJdHxgup8121uZaV35+2v3rB9sUh2iT8t8fjkrPqpo1fuWx6Q9pH4oRNDyaaC/pYsk5zsAGRki9tWN408s6G+TgouyKu+Ok1e4d/bqaMCiqooIIKKvzXQl7vRN1yagTq4hKimaeDvqCFZbd+Tm1Cu+JNoZLnIiyHzEclBBLRg+21eOeS8m9nlNqXE9mm+jo2AaOkbt1nSIRuwmIC2stLCwSCuyyKJD/dQtDAAPdfw5cujrBjZz8GIKa2GP7HLuzGvNQaXTdfQ2GptJKbUTdhm0576rNqb525WOA658owCweUpV1T/Cm2rntezeA5MwZq8y3G+uu+T6gAUCPHRPjz7IKbO+BQjJpaCmh88Dgr6fPpJft2xqpHnR6kzSp7dXpLpdv29aFWEIDdlJdI0A3CGwqHf2Sfxq59tXfKW6dbJwbheJYyaipaIcZ9rFX756qgggoqqKBCr6Fg3gml/GW1hvdMY+HLCXJRQhXMM8pC5p5GpPKvRRpOW435rbG2+2Jf9pT1c9sWbj0/Dq8nY+YF5VtqNdJplnBuLaPpSzGJCqUPnBBiBwPYdcUpRPQQJ13+deT0lCp1+ygH4Xe57S+v3Kl1XaWVfmd9TqNO/60ZfhaC4YmOqqwyegfWclCgdvdwBaOqoLxDL3i+ixb/TzaJ0ETRwFppQWSe35J6+QjB5YRm+uGz2dVIn1vn/Rz4M1+ai1IKYfYbzTUUnUbJ2nHyq9P8ZX0R/JNolQ9TCIb+ZlqqoRMVVFBBBRVU6DUUzDupz/zKsNiE6+qclKekMc0328jsnNDLM/NpFtF9BOdCMJM3nNEw3DTlxELP8h0fVgcYSXRQ6PVv8xmO0TjhvTpK3zSoD1g5NVSfd15L4YdiLY8DpvyeC6XsSSHTfoatcE0UStHtNCIskATYj/gjWPTrXmZtfl4D3H6Gr+h22ZSCnCYd1wBnQY+B05qcVI70mOStKfN8SkZSWhM0sA2wnzMrWOSFDCX3UyHdPNpNU9FppPz4O21We910BT+0Zt29UAfCOxoh5HpXBRVUUEEFFVSQB7m9E05zYWqNnqczStDgMquyswkGvp46sr5B4bSnpRKwXta63Y06zGj0kqNfTTf6Hj5/bVL/NeZQ8dMLEwl6g62EtyaVf8lHBV3yF6wMQs58WwDBjxZ0KRiN2e+JBmF2XaXSmovIcGffAUHGEu0+JSe9Ee23LFB0ZTdabUo1x3YaTrBSK60sfk+eyYojPhiQzPNptdVkhJXfWDdjsW+AmY3vs9uMfewNwQpOYzdXFDfDcSaCb3cYZReuf2kC0P1MVZ0TFVRQQQUVVPgByO2dUPJSK5l6I6gfb10wHjHTll2YXQ+gbc3BhMS7z9t9I0cbiXQ4KBWJVSxMOD3+drxVkMmdc2khi6ODtNSdBo/9v/buNqaNMoAD+MnRAl3r+rL2OqCUAhVWDgZlMKQDhsThgK4Lw2DiC0w3kOACiroZv0wSh9NkbMyRzURD3BxT5jAQo+hQ4iKGxop0m4izHSBusvH+UmhpOwXqeGlxxi8W8v99uzz/uz737Z97rs89cv6Cr9MOZmPduk4rf6/5u6Of+u7JkHa3X7UqCmPmSsRkV337VPhuTnNtg2S7Orj3ShchiqbIG7qPP5hIKI5mi73MWq1hRBW1lrAPdTZW6ak9WUrK0vtNj2e8Rr6wnNgnulsH2bQ/Z6ZXTBmOVzZK8sv3h8w+kpl0zjN4fC9Th1Y/rkpmE/axztN1+oDMrBTGb9/+QUjklGe/7viXE+rsaFcxTQhJ2k03jRO2VJap5ULDeIyMfdUecZ+usp6bu41Vc/Ttr/zy3nmc5mKhBwAA4N6Waye2iV97Ri2Gs1VpZSfkLIIYtkzbpvVHEovjnikoKV3PWJzt/XnU2n627qnXns/y+elEW3VG8fXc2HXm2yOygtJH1y153GIb+b17wGo4/ElabUky29bX0tovSQtyvBsy3Hnp9pT+zEe7Du7XsImBaYvVpi96rjgto6AyZz2T5JTulCXVvJR4K3mjp+mOLP31J5QU+dcVr7WMiPOCF606mXovG6ZHLbrvm6dGGpu05szymoel3o4ZOOc5W3J20vtq0vf17QpmjN0J3L33yRQ+SQxbzTbbpYqilLjMN4pzAhkkz0WMaVFuTyYrni0qPBckScouzLv1ykGL8fD51DMl8Zzxxg+/0DYHxZQ9hnYCAADwbyzXTkhBVmlFFJ+OF829ucrdceBYvYGMUiokTv9DIQXJJ4/IKTp8dmjTqdO1+T929BBCZeQGmYut30nfpBcvhvBU4dRsV6ByD72bxnCsnJDCrSffkosiaJnPzIlC1YGvDxlJuXKzYxpsVf4p4xaddtA7lI6M5DtKEilO/7z6QaZwYQ2y9Rt/GRLvePMB+6iXouRlNbVgxxVXeWJtREHrucSmjkFWAJ0YzHfEuar3jpVf9gh5SDE3W9cxpr+moVrWdJ0I2xgRyiGtgy9crOI7bpC1re59ed/9gaFO/3UCAAAAV5Zd2fEUhcWIFhx7iSLUouWyvE0xvLtHHt5UbDwV+w+/yQtLnY8TXjxf6fyYYHOcYH6MSSWoqEUne3hLaZWUWIIpEC+OEZPXrvSx5E+rkxK4LqbgnJ+5NEtMq8VLkxJaJbl3zIPtF6Xx+/sm+BtS+XeHSK5/iKs5AAAAgEur9Rt104NthsmADCk+cwMAALDSrNJ2MnXzh89uED6TPW1dTEWAcA1e+AAAAFgxVmc7sZnMoqJXy9b4eAwMjVskQpebtAAAAIBbWp3thOTLE7Ll//csAAAA4L9Yne0EAAAAVi60EwAAAHAvaCcAAADgXtBOAAAAwL2gnQAAAIB7QTsBAAAA94J2AgAAAO4F7QQAAADcC9oJAAAAuJc/AQ4pF/BTGzhYAAAAAElFTkSuQmCC" alt="" name="Image1" width="643" height="222" align="left" border="0" />
三、 四个概念
145/1594
Python
programs can be
decomposed into modules, statements, expressions,
and objects, as follows:
1.
Programs are composed of modules.
2.
Modules contain statements.
3.
Statements contain expressions.
4.
Expressions create and process objects.
四、变量类型
Python’s
Core Data Types
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAmgAAAF6CAIAAAAiezMTAAEr40lEQVR4nOydBVyT2xvHX9YbG2PB6EZKkFQUBQTkWhjYYoCd2Ncu7ESwFbALu68K2IkiCijd3YyNdfy3ERIbYdzwf77Xz2VvnHOe99k553fyHeK5+BkEAAAAAACgYyD+aQMAAAAAAPgvAYQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBOAIQTAAAAAIBO8AuFk1+Zn5HC0+xhRITLvcTX6mGo0urSbwKvJj8+l29kYUj+x56wDf8DAAAA4LtpSzhFtRUllUrKeKSSUqtrYhGXgyRp4hTUyfySmye2z7nwkeO+O3ujE7HZpeJroVtnRXwWe+3LXOtAlB++TUTsnPRivLEhpX1B4FcUlMI0tEkdkQ4Rj1HLFTYcwZEYZQwS9h3mQfycZ8f99kQ8E3tFXVrnif+eKH6UNvwPAAAAgB+iDeEUFIev8F1WZexsQMEjlHhlcZEZIks7e0M0xK3JefmVPmjHlWu9CPLDItWHT/K7c/9zvK1+S+FAaoz097/1YFmqrc73aIqI+f7CqkEPu0WGzWhLOIU1n59d33P5ekS525OzS3tj249YUJVw8uqD89cfxggMhnuaoekF8VnV6k4TQuYM7IZrX0BrUy5MOcteuHJabzxS323KupcPXufZmnYg3VbBOxqkLdrwvwQR/XH4zjDS9BOjjDA/I7V/kJ/sNwAAAGifNoSTkZ5gujpl8R+GSMkBL/6Ev02e9tZNu4arSA45sWd2RdHQbUQsqEqLZVDcusgZJ+SVpXxkUvobf8cQIjvhzv6Flz8zjEdoK05cWBW76+wbsYEOvqqaTzHVa8vMbyAoDguma6M+PIyBjdq/YqguHOIV3vGesnOAUDNpuX27nTYei86AVOp74Pyy2FSmZg/jRmkXMIoyWUQTdYUK3Cz4z6AN/0MiTkk5C6mD/q7+tKC6qKiGqK3XgcbE38BP9xsAAAC0RxvCSXDctQBDQtYdcLNSSiFqX/16EcI4TFxt0+Y4LzM3Pgdl4KYjp8/FyInLRhr10e5sb4eb8iAsDO7pQ40sMtVQVnwfnOSwaoEDxE1dfRFSM9BW7XgNzy2OLYdoPfXqhnZRGr3GGkCRnz/n8uytUe0EJdnN+cuu4YCV87QYaWWtg6s/ZkTtm7dMb0+sv5EiEW8W/GfQhv8hhPr4VcHjvy9eRuzc+YfMd4etN2rPI38LP91vAAAA0B5taB8CR2q8yiv7XMBDqhvrNFb8METzoCIOo5oOKVMJaJno8PKSM1nq3l2l0iFiVVUwsBR1TJ2CcTISs3maI7rioOYIGBXVPDyZIr8jxM95Gr6vtv+e/syA43B9Sd+t3UfjlX2phLS7aHR4uFRiaGFiJaRr3hCEV5pUBRHNumghGp6RXs1XJhPkOo3PKOGg1QlSOWEVJnzla843bLCRmXwuDuYyXKOtrm+T4BIErOoauApZ5goeo4KOJKlhFOu/gFVSwYAR1Zrc04b/6x+Eq0wmIppFUlzNVyUTW6Yj4lZWsTEk1boeJj350VOYzVyNpqopZFSU12KpGgr6fUJmST5E1cfxy8qZSBJVFfktSUZVLZIoTZHHpPOwRHxjBC2NETBreBgVnBzHN/dbQ+iKUj5eg/h9XWoAAABomw6uquUWfyyDNJw05fTzRKyER2dDPpayatKuv8mmDjmQvMwGD7GSEytIFuakoui15yJjCnJepWLm7dm/w4YAEzG+JFaSLSy0GpMWsZOeXAjLgKuyP4Y84AbsC95g3kLshCUxZzZl99o1yRRbcedLLbGXZvtqyKvMTufgrXRVOr5wmF2cmgcR/9CVrvUVMjIvhe4+gxt6IqAnBQYJ6QkhQdtXPeXNO3IuyFLaV+ZmnHHfUhS4f4UXgZv++Ojkvdcy+gSnr7InQKKqrMRiFcvuFEnK7LiI/Zuev71ZyXM4u2Wsvteu2e76LQ1qFlyZlXH68K6ld1JtN9583LPqzIHN8+6lMQ2nxh/3l9Pr5RZeO3vqHkvdnKaU8up5oeOSC5O6kaRyodD/ECvz1P5N8/7iLT9xMtAYLXN/9uWLd+NheGbc1dPckdH7pjhi6yO/f/fh8/T4iAexNR5BmctUwvefuv72ZRHfdOuWDRZec3a5q1V+urErMiUr+8ONZPW9J44u1m/2DRR8jjx040boS9bk5aOU3n+IS4t7Wm66Zc/2VeY4IT1+767NK1+Rwy7vMn+wfnB42sA99y90l2OMLSt2x65t696rhV46NJ0Gh3iZW2fPOmq6I3GlVVkzt0sfpTb7ya57GXA868nVB+wRwdFTunC+3Fl59MJfSP83uwfpwiFu5hmn2bcdd5wJs8dBgoL986fvM9wav8JewVw9AAAAtKZjqsKryEjlKOl1obUcXRXSn54Ouqg+JWS1gTLj1bDRayustKWdHE7hmzyxkX3B6XeU6ct2bIGXhAeMCzgft9LGlczJf1GgZD5ct6E7xv16a8vs/OE35nWnMAzf3l13M6FijblOE7tE1YkXlrwy2BZgR4FDzOLUAiV1O8325y1ZRckFEGWiesdmOGUwizJKIH7i9Z3DT6U/+1yiN2TVm2OeUnHhFd5+XNq9txb8ea2VGqre7Oj773le6iiIlfXsEdzWUfkO1E1X1rDgpMUXwPR8zKTOwtqNXbim6uO92jHnt403Q8pJtFlwEf31w1iSex/t+5V2pIJjR/9iuq28BF/h/bK0WgBBLYRTUHJ++/JQ08D7040lzhS6q3tM3rzR4UyIFVah/63t0p6n6TpqY54JHeqmqLnZR7buSRu2Nag7scrwa9j6Fy8rJjnqIETMr7t3RaAnr9wxcsqmWbmZIg0iFrVk4eSSj2/oY9ffGqeHkga9PPks/ODONSYwxudXn5Qozc3jlccz9L2Neduf1CSVmpxbNYLMzwicPmVT6Ntp202fRRY69DWnJuEIiRFnBO5Bayd72MgzpuSPkrgSOzcL1XeFLIFYGi2KaklBwHAYXku3Q5zsm5P25s/ZMt+LyLD6enfUy/i8AYxXhZp9VJknCtl1odFUA00kWruur40gmmliVbXJ/4pBZwAA8J+hY8IpEaF8iOyq1WJBCD/93q5NovG3Bhsoy9a/5PFpXgZ4yT0iRtbbciG3jDhuvrOuNAkclQDn0mu5IkhQnR7HVPM2wjeM217yu4Raf8yBIii8fPxkis2MMwO0mhrFK7zvtylKdeCAq1cvSQ7ZWe8LxfiY+5fKqfbT+5srnr/kl2Tl0tFaXSnyxEo+nLz0EgHZY8/q5a44YVXG43Xbgv7Yzv5rtbcpSsvHhxJ3/DhP3dNORZqkqCYu6G6hak9bQzSEM/xjNuG+K53Wz0x2TVD9OY2p3cuo3jZhVUxsGc3GSkeBIc2Cw9B9fMbQ320oRGtAL55gRwXM0hW+fg2h1FovcRIVPw9e8MXxzgrjuiYInGTel1x66WMxz8oQocj/EMFpgFfBvWtcNTdTWbc5PmLrXpT/Owciv+jxqlO5rtPX+EncL6p+cGjLVZPNL02kfU+Uqp55/aMkRZeT3BraDlXJT55m6n2hC00oBBsXl5YPhtIa2Idw534JROgdMLQbWeINNK27AZZbUM6AeYwepVVw7xaf1CWm0GGrvwMFJjPmTCtj9LRJBtq1CcnKsGIUXLYrSsDMq9Wc0N9EzbBrM7dzM/Zsi8D4HfMkCrIeH9uYa7tlzUBTTYK5JvtVIgZejGgIXVrCg+o+QyJOKddomrtOJ9pWAAAA0DHhlIhQHgOi2jfvvQlKIhddhi84aCkb5uJnv3oQD9dfryWtj2vz4zMg3UXDe+rWxc8riy/gUa01JWpZm/8lF6XnWL8itybqzNVCm6UqcVfXJJaq9gz81Fsf30wLBUXJ6XBDjYrkT0+kh8KK1EIIY5qRmMjt2RMDq7y62n/cq2rZ5kuE2diDsXMtGwaTOVnJpRDVRb8TvQludnq5kpq5gdQ0OMnYa9ef6fdmBS9w6XXfkwITVr2LLSV1czCRXuV+vRN2kY7o62RYlxwj+0Ma1jJQS/ZQnLw3JShz84beOTPtfh7KwU+/3rDKp8OnbLxVLZKZrLv0QNgeS2yz4BAvPzm9kotk24+boIuChEWfvtJ1u1uqt5hAFJbdjniLdAru1jhoLRYJRGIhXyhu0//Spkh2DdHIVFMi5DWxW66WuyxRfnr1+Ksy/KCNJ4bqS9tGnPRrfz5XW37KoIWiVKe9TUWZrdOrT5JqN2KIcPPwWYy9G1cutJL3Lgte6YcctmbfYS4qdTazCkq5yhpaZKlVnNT4IjaT3NXThlL3jSswpu7JBBAcjZDKnaA05iltbIjsa2jqt8rY0/vLux1WjgsJTcjH97oc3tu8IbTEJxAciZSFznkb+ZkHGw2THggr4h6ThuzQBG/PAgAAnaJDlQYnK6UMIrqYEJrWjbzkvyI+GMw8W9exYn3ZdylVqDHTTFqpCkrT05hGg8fo1KsWJ/fJuQLKsGWmBEiQkZPDJLvU7x9kpV35SEe5MiAz783ucvc3IPQ9Fl33aDysub509ALNBdeWdZNu22MnfYWM+jrCpWbBVTw8DL9NwfKrE3NqkepGWh3vTXDL4osFlK7f3paAUdOnQbzUtDKOJwXHTLmTg3LyNSFI5+6i9yfB8TC9gaayvo5EcT8nc/T9u8oeSkDPSWaTh2s26Gb22498vQ0m9abVlmRDhrZ/1JlMtB9niG0RXHJLwqcSZbslK51km1kYKXcLVNzn67QcJGfnPcsT6gzV/rZIilv8qQplbExFQ4J8hf6HpOuGsmr1XPXw0g1HTx7TkSOYkIP39NHf3M9NeRadThvWu+VrI1hf3qVy9fxtG7yMUPc6dwyts2HT0nnTv2w5fNyF2lI7Wbmvy/AuLkZ1eyxF1QlXc7Ae4y2le3v45e+TK7Hmg4Y06JYCY6TUSR8aDoNEjBe3PjlNXKULb+F21qenH8uQrtWQ2Yxp7s3bXpBAIIJgSITkJCPx0P0CEaSGQ0mEkx17702XYcvVwQoiAADQOToinAL619xaiNrFoGnvTUR/97YAb68m631wPt+59oEDkWzMtKQDkuyU+DINu671VaKgOOL4tarei9ZZ4aRVaXoFXM2gflUmpyKNibZ27uum1f4iWSm8ii8lQg039fouD9Zi/bZg+XdyCmNKIU3HtnattIq86KMkyFD1xi5cTfbnbAhpbUyV1MzMnPef+AbrzfGSVsTJ6yVO2owTFKfeVNkTimo+xpZrOBrLVuVA7JKMIpiaJaXuCfl5CQnlVGcH1XpNUbbwv9nC5ObBIVZ2ZC5h5CoXPVnc9PQXsXCreUat/CPms4UQCoVorPYrEyMlPdBwWxXpWwEU+l869ZhQQXSV7e9kledXo42GuNk2j55XkFUhUqYQW+QNfumrhGqtXmZqTeQRrem6b39Yl/VzAk48Wt7Tt8UkLqvoS5pId0396mLul3sX3mmPedaLLFu9lPmklDRsoU3jxKgCY2QeEvAFSnCEkqg6MeIQ3Cdc1t1s7jdOYT4TZ9R7pK1WqxchiPg8oRJSorqs11euifv11MzMUUYqsdJu7GX8cdDkv/4GCAAA8PfTEeHkFEhEiOioR2l6s4hTxeGV5RTShfr5T0P3c7rpKb3gmaFf3rhDdbOIyWTTest2jIgYby5s3cwbd3tdP9mwIacgn4EiKyX9de6+xWg/Cl4DzY2JyaD3tiVCoqqUh4fj1aePsG85LPnNkvx3lThLbUK7+9151ZlJtZCOSfPVTNzso/sOPtb2Pz7BqvXkKLcsI42H6lK/bkRUmxO5aNcjrt3MIBcqDBJWZqcUw4h45pdDF6NRw3zxIedQBhbit5dP6npP0ciJzhOoD+Heu3LPaPBgzfK8KiRZKef+jreWiwZQUhOKIVoXPXh59LVHNc6jfTRbTXWymgW3KP78Vmi506xumSf766vPtQb+pLjLobRBM8ybiAJW39MAsSu1kOWlKluNlXboZGLPuQcHSR6MV6rY/9KOaTzPYIqsB4smkLHcpIcZzCG2eMmdsY9uvKR5z7fHEinKguTEVFY/NZx0nP7htXtFPSf4U/JeFUO6XdQR5bEHImvduqQEJXQP8rMlYwx8RziF3KASWrpURM/5Wow37CLbZcLKuLbgIW37Nl8bmerV5n9ORnSdY/LtiRQYI33Xr1goEInYmZ+uzLkrWrjemijHb64kMpqVFBPP7O0mDZ1y9ka8nvcI97rQQpGwtuj51aAw3vAjdlEXRZy8pPsLbhVNWDNWDXQ3AQBAp2lHONnxd88eevHkKhMSfrm89Ej22NEjveq6WQg1t146f15Yrz+M5jhwyZXxXN9Tovhb1/M2Lx8I/xBYykt6ELGXrlxeWFhF843a2at+ukzIpXOF9PeXb/XfuF16qtvS4YauF/90KXWzQbDEhoO2TlSsmpKqsiA+kUNeqN7WvCU3P3rvX6lFmdGJEKT99NzqfC3P4WO8qNJLIkZSxKOYp0YOm8a1EE5uSuS53bevpUK8rMNrfR7ihbVVhbU4x1F7EoY56MpSQ2BV0LwYv3XKIYErpulWH2Lw2VnnjrsHHjTBCUvyk2sEny/cmBy4eAROmF3L5de+3/ey/6WZBhiomscX8uODXBb2mDZr0dLWqilxSW2z4LmJbwtoA6zrel3Cqg/xpbUZ5/a5BYb1ad6VQmhNXuR/dWPIn7p+w8kVjx9G5/2x9cJALamxbElDR4H/pe2D1FySQ13nU9V63FzD+buWz891M0axoK4DZ6yWCZXD0BG97h8fsqjCxxhZzSL0Gzd9liR8tYArFL7YN8+9h/eOhWN1098+ObXcPXOAlxq/gK65Y4m7VssvjpOeUMitEUR/iKulx1x6z5u+bcOE+jdoCMvTEys0BnZrMiCgyBgpSkqQKHXVHvL+kE0uDfrc3G84w7HDrQIuDgooGWmMZIgNpsyY5N4YWnJz2rF5Gkui1jqQUx7DxDmbdkRtD9ru/c+9gB8AAPyXaUc4sd28Zx6T/JNzCdN92uGPNglVtG6uRkSEiHk4+DDWzNJAumXd9e79BxU1LBGaqIZv/p50uNqY5SE9qVYO5DoJwfeeeSyzT2xMJcbMqls3cjsrYDEGY19dn6ah2pbRaB3P1TM8IWjOgVaXYNQ/bpzpUqJi0GpbCNrMa1qY5J/CWOFanluzrJg4GlXW20WN/XNfD7KVU90SJ4rb0aAu6lZddWVHOu4rnlhSnc3qNjmoDl0ZcjsDbmtvqatgthXePLjegO1xPZA6dVU6nDZ66W47UjdnTWzrrhHBYnLUSY9XH1OKlfSmrNhr2vj6AKJi/0OiyvREyHamRt29eOvtRyOGxyYVY/ScuxmrN7gFYzzx8UX76IRSmLqZi7lm/ZShau8TIdsTYCYelurS7qrjsqQrQ54llUBUUxcLLXxr+4T0hFSG4ZA59uJanOXosCHkJg6A6w/ck9Cr4TGhtoyRpmwz5+Zmb6qto3WTFUgt/Ea0nvXukkt0UiVOz8rFuOkOE4LrnO23fMiuNvrS8XKLyZe3uhKsHWxajkQDAABAB/mR2gOhatezYRMCDG9hY9V4BYbEqVHkTlsi1Ezt1JqegGH0rXrry7u1NTAsVbvj7wGSA1xVx0T1+4LCMOqajeO+CJq5A63xEoLk6ED6dqRq2rdJGmia9ZBvt8qjeXAIRTLU+HZNw9JJQ06YeuA4Hdc+OnKMVeR/YWX04xp3P73GJ4FhNHr1lpMChmo52N2y+TmUrlVv3SaJ4GgWA2kWCo1j578qQdtOdfaR+0sAKKJ+K7coMgbCarm7arU82cJvEns0rIbIC62sZTe0MTRKvU8fdYU2AwAAQPuAZvf/E8zk64f5/U/9LStieJVp8Wz1aXo/1NIBAACAfx9AOP8vEJa8PxsYlfo+VWnaRj/Tjr8T4vvhZn18mwmhmblpX1EG5mpyhpoBAADgvwkQzv8L4GpW/f0QPf5caG749/wcmJDLpo04G4hRhtWUMgVmau2HAAAAgP8IQDj/P4BhNZ3sNP++9OAqts59bf++9AAAAOBvAwgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACd4KcIp6AmNTWjCKZu30WLAJeeEFYnhN9+X0a0n+5tqw5vequQWc1CqhLQPyNZwH8ZEauypIgtajhUwpDUtXHwtkL8FITVr+7djqxW6Tt4eF9K2zdK83Cpit10bzsNBCRgVtViSMSf19BsEb98RKzUhIRCoqWLAeFXuUbALOVgaHjQggYAOs4PlxdmxnW/lcHXS6Wf0UbDLuxcOIKGEFTFBoWfStEWeQ9oKpzCoqhVZpvfavke/zjLHPejKQP+09Q+3uM35BWn8dhhyZV3w9R/uXIKqx5fDgvM0+Q4tSOc9XlYgzdwgB25+Jr75JD35gsSQ0aZIn+OIU3jVyScosoXs5bshq28FGlA+DmptoCff2DhpAXJ5iGnjyzQ/SUpAAC/Iz8onKyEdWslqomwch3QtSgqIu3W5N1dHXcMUJd/txIcjSNAGJIyEtbhBL5GXdz+V6rJjI0bzLEdOA/4j0Gx9fRWl2gR0tQAq/RPG6MIGByjgoUIeAxSYiIr++LFsydTdbZtnOL4a7OeqPTzw3eQxRFbUofLS7s0LzhKcGVlLITDK4MOJwDQCX6owIhK3509Xgghu86/uWGEQZVN9YStD2MuXy30nCf/fhjNZWNutBCO6HC/QlAdeeH0uQzKHH9xh84D/mPArIcvOuVO/KfNaAeE5uC/bvevy7iC0vc7z0R+pgzb8Kuznqjm1aNEgVmAO/nn9cNbFByE5tTddyZ3pkQCAIAfFM7aj88SWRBk4+6kj4DgFPvRRtDDpKy7Kcx5xrLropqnJ1dMjMpEW40+smxUdzxU8mKXz8l0ssfyyxNNcRA343HowgvPPzJVnQfNPjzBniYtvSJm5qONJ+89TC2BmwwYBX95KENysuLC9rkxup6hgZPsMBDELzy5de2OxvM6TiOUP13Ow/wRsH2XDab4+c4Rp7J1hi9fxQmfGSUePqln1qVLD6vVBk/6M3iALkZqltx0Af84osoPh0YdjWMb+UYs70fJODNmzzOG+ZTLcw2enD566E1yapWSVpeeiwPm+hlgOZmXx++IFLlMGVNzY9fTLMjQfcOCIbzrwVufZ/H1BwStnjaIIky8HDhFfgZoSocyg6Do/uTAK+lqw8Kmo7ZtOh8vOVUR5T8vycxTmpNhBdFr9l+8nspQsxq0c8lEdxK8zjyx2/Sx9Cs7k6yOL9a5dvL6veS8UiWqbc8xwXMGWjbvqopY2edDQ3Y8TytH6AybFXjYQ11aLhmJ5z7zbWY5aLUoF6ZjT04Ubtr7Lf5Te/zNy1vaAPHyL55o7jftqmYFR1Kg1nt+3hsYXECbtXrzHH2JGZmnDu/f+yaHq2Y9ZebilfYkODdz36btF8Su610qDl5+kcjTGTNj5Y6+mmCNAuD/mx8RTgH9aw4TgvBmerI1EzBlYwMilETPz63k1Aln0c1FV4mqfHr1k4MjVS2+LrLkVqa/yUilmbGEkLDo2fbegY8rdexc4PHXwpfTaecfDFBnfT3pEXD6gwCiaOtrivFUIlEFARULIGUCSUNVGVU3lqcEU256nkQ2xFZ8flxa+75gk412yps3bzIE4zWIgtj0DynFH9a+QhPxPHrBse2rKQahW82RctMF0vkPIWJVF2cUSHIRXIVKo3SxpxVdiUg7f8nX0f7alfupAp+JljSlkvjYTJGGeU9M/J0Pt/xXYC1Oz7XiVXxOSclKWXlXmabFL81/FzFyxg2EkqqGoCL/w/mpYd1TVliyK+RlAKOmqcvPhK0zg5BT+jEpI6WqmA2ZUog4JFTJgzBkEkVNGSmueDplXuClGh33bvCXz8MH19JSdg+k1JmXH3i7limmGXAYGdGZYgPzrsrxryNvbffG6CfOtWySCutN+IrJ14uIBnZ2yBouFltXKKu+PnrKMdzQnSY5ZDQtFyI8QZjZNH52uRwbdEWMln47MUK5RYEScfNSkz7nVedwpK2DUxvmTIthq5uYIpKerl1aKA47tFabV5ye8qE4ZegrtBZVqbA8LnjnQRebrSNIvzZbAAD/bn5IOJklkv4mhCZh66ZgYDjZalkWXaKLMuCW+0/tn1R2wGrRrbynf32caWnQGJaXd+rE4xJY1yN79k4X3+o1PiTq2otsd+dHB899EMB7zgqL9jWWrh4S9OF+GbcogzJs/tbD1g3LiRAaYwL+LEr4dp4Rl0W7cT/rU3oVXzk+rRpCOgwzwaMTpc+GsFyYGPJHbshkz7s5Zx6mrzbCy0m33yhjMMfzDxETPMNE+pcy68D5o90clg3ViriQcfJBVMwrOqTlu9qJDMOQtx+7AEmyGPvL4klzgotf3MmbZoNES9fowK32h4ZMLN5juuSvUq5pyLmQSWUh5gtuF8Z/yuVZodHyMsAc5W9py82EbWYGhLpHyLKKV+MPfKb0CdqytDeO9/XchktVsF5L9jwaDB2dOy4g9tqNYq9ZdebVsq2Grwmf5GpPxcaclz5B7ZcDFnOvZL18nTrN0uKbGQV/vS6CYN0O7QuZQG48y4yNiqUbTBgg6XwKCs81LxfcjBNN4u+JeRDQ2oYF2hYt/VY4bXPzggPxsq43pMfJurcjhg3p+D86Mgl9fZb5kdRD15IWLSLIZFzJcU7Yq+GsdX6zdhV/jcqHgHAC/r/5EcFQUoLJuoDi+skesUgo/YRAwetXedDsnNVQqqp9XPC3LlWlJtYIDRqCihjJ93MgiEgTZcRGibmqWAgqTskqU4lIFkIop6UDjTu15pZg4uqifP9ablxyNVVSBUGGLj1UYCyZFXq2VjooAtW1m+rdJ/lJuVV0WOt0c3gQEM5/Cq3eI3x1UJIOZx+adImQ7dDxfSL2vrx4NBlCeczzsasbWhVVf3h850Js0hO65ICRyxBCJFnWo9n0pCKxfB0KBJWSTGxISBy8iyYEFdaWV0k6Z/IyAF30TbDkZsLOZQZRzYe30ih0RZlRsWI2XhpFbAmv3jy8y47p/bvL1sMKqpMj7kRGJX0slz5BSaWwSSRwkpkGEiqMX7H3iunKkd0JsmYoK+3ie4bpqF6GSEhUkdiyXMCaxK9cfkauDdoIOX5T/CQVqR/SIUjN2s4QhYRZ2ehA6flJKcWCHjIvqrl0U0dh2N0kji5mFTE67B8A4PfkRwQDjqdJp2rYFey6AimurZHuLsCrNqzRg8FlbX6CpqS4M7l0TuOmPUjAKKuQiGz1k3lrnjTEJuDVlJRKYqLo6XZ2saKyxRhL1LX3Sa/SdBKYUJdeNpoIKKPeBOmQmKTmlFRf1dyaajq/dbpCkcKIAb8YmKnXlN1NFgchNF0XOBx4GcOD0L3m95aNmrKSt/05f00iD69hpCPVFJFA1PCF1WUwJSVZQw0Gk67bhktvEYsbF+60yADMJt+13EzYucwgZObXSKO4HLz6ckMU/MYo8Jo02d4VRvLZgQGhr3hYAyM12RMIRU1TgVNHL1p0Y/HuGy8P9F5YdG3X3CFUBDM9+i+69nRnLbSkR8pQUC7q4ldkQxt+k4OAXsEUSwsvVuIvuLIqXnKOVVktqI8QBZf5UupoMViPB/i/50eEE6FirqcMZdYmZ1bxehJQQnpytqQtiu1iSEY13CItYyJeDV/yB03GfltUD6sby1IbcnXrCFOZDUpIoh7sqXSol13NFHTSEphKL3czxPuUh+9icyCyr4NmkzUgdSawuFKDccpoTut0jcCW0n8Noprkm8k86SduwoWE6mF9lFNv7ZTU/kZj9n+YYxi5cOjY+M5G2SwDNMmD8jNh5zKDElL2zga1mZu2zdepj4KqhYOK6i9LhYafc3SXRDU1l+wP223w3n3YxuetosHoD7lyUm/HxlVrP16dfMAxI9Au9embIo1+w3SlBQKGwiooF7L45duATL7RKb/BMFipM3hsvsRfYh5b6i40XhlM/gMAcvihIUplO9eu2KcxX6OfpY2aZFb29mKmpG1qPsJUGaqRXacXFPMkTdnUD1UQRDK1aPLyEwTRqBsBiq/MKVfRH6nZYATL2F4V+lT98VIKw91BNmKlpCTb8slj8Jqn3PI8XNPWvRuU8PrhJxGuj7ehpPKrv1BRWMmB+MVfv5ZKqhZjXSpJKCddwL8FQVb0mcs1KDffvukXHt04G5nuNDAnpUSiLNZ2xiRxbQWn072dFhlAtYlwys+E7aGkJNu7wWNxZFFYGROgzMokOsHCTasxCm7TANziWOkTGLsbEcS1NbUKngBOtFm5cuaNMUGxWRklDPL1V2W6fdwsZKtXEaqtykVT5NvAjJfrN0UFCkJQDAxJUEZhSlaFsCs6P7UQgogGJpo/6W0PAMDvxQ9pB0zDaeJU9ZhD6aH9Aj6bVL5/JYS0vSd7U2HiSp60k8mMnrUJ3asq6jMEabv0t8NBlY1B8ZZz+mucuxofsGJTplcXZFkh3HNuoI357EE6Jy7kh62cX9bPSkOj/w4/Qz0NLJTGiAjZShk2cfNIi/oXqMDxLc+rOfjoQR9zxdgenk74byZWRQdNRJvmRWZBEHnoH10IeJi8dH/Na1kA7SOKObW2322JEsHIdjNOjhYevPBFgO45b/jouKePtidfOpjsNcuYCj3JjjwbujWhJCRVGqZTo6ktMwBU9u2a/EzYTmaA49X1sdBHxuMF24izJ0yfMry/QeTVF8ErfAv/sEOUZsA890y1bTakiqJ1o0IR2e+3hp15VXwlVvbUzSYbhRU39x95omJAyH0k6RZSzMxJJS+vF1MG9zWo7/3iWpaLQNem4fE95dhgqSPXby0KzpBvQzNEC+9R5KjQpNCZRwrxzz9wIerk4daqTd0FAADq+cFOF77b9q0LS9YfvJocUwxhzdxmXJxnR4KgWj5b0qLV8pjYPfFcRCmkajP18kxrAiQq4UoHm2AwSAnCOc/cd0mwaf7Np7vCnkJYzaHG1Twb3e5T9l7nb559NfHW/SyMldEy324e/n4ecUcf57wIeei0dHhjr5XQ8jxK3cVKFcplOHl2ozZpk6uaqsbdf1YIKffx27jTRqqo8tIloOQ9HOBvgJX9OTpb+gGvPCLvzZ2wUkjFZYiHupH1UJPtR9NPnPuwfPmCJc9WBH29ubbAbkZftdCnVVXsTihnywwgbKoEcjNhe5mBYL9hsv3TYx+/vrh6psfYuUNnRW0Q+gbfuHIx9AqENeptXMq31W96P0pvRsCYqysvv70Zlm7nPVrt7pUqRm3TJ+CXxyU82Z8qbWpq2E08M8eq/Pa+DNWe4d9WyGFblIsA52YW4a3k2GA+RK7fVJoVnEHWTWKx3b0joGzNwZtXLkBKmiPnb9xli4cEQDgBgNb86GgljNBl5JXzg8vKqiESTQ1VL1nKXRfmPVso/SSaVFotppDr3t7NZ1RLx7dwKrIl7mjtsYuPjV3ArmBCqkRsvSCiNH3mH/aZ0+SkiW/0bZ/SKg5OlYRvMuOCa3GelX3vUzWEcpzq0Oz9ZFSnZZ9CKEyIqN74AnG56QL+bgje2x61Grbsw/Co/0QZf0I8vv7z3uN/ralkoklkZTh0vP6cf/Iz//qP+hO/PJtY/xnrHfPMW/aJ90X2p2UGgBuuO/d8XWOCijMD2rBJEk0/Qxgb3+Ayn6oSDppGkkZq7LH4nceCWjoTwhPrJwWb3Q9Xc5z/4f7kYiZSnSxJYnn9aZVv9ziEPlpBr2IiSTRJfKLK2+W0QUMHOzSdbW1VLprELzVWjg2qjvL81rzgIKAm3oARzUbfuOpTXV4hUlEj15VlVFN3YcYdej4OAgAAP2WaD4ZRU9dQcAlLq9+aJuIUvTsWXSgpfpYWGt9GiOBYSusXrrU4CcfSqPIW2jacFzHTju9eu7sQ0h/hP1ythRQqwXFkOe/OlZsu4N8JDEWmktu/TT4KMkBTOp8Z4FiSVrMsCVcmthUFDKWi1dYTwHFEasNWE/LQZcFDv8fOVjYo8puiAiUFoUptx1sAwP89f9v6GFbc7FlrT9MhpOnY9Y4/V7IE2Q93znlaDjcce2qqFZiuBAAAAMCv5G8TTpSOz0jfLuq9p3pa/+ylegg959HTU8snzxnn8m3JIVzNdvTGSVVUBzJYGPh/CcgAAADgF/G3CSdCfZjf7GG/KG7N/qGrWpyD02yGb7D5NekB/gOADAAAAH4RYCsjAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACdAAgnAAAAAACd4MeEU8SpzK0UkmhqRFk8InZFTjVEU6cow9oLKT86ZtyDGw9gfRYMMFT+IbsAAADg70RU/fXq9lTbtUNNpT/RJCi/f/46vZ//eG3UP23Y34qI8XX/+VS3yUPtcFIvFL45d7DWa0M/bfQ/bdjP5seEs+bTPpsV71w2XLrtQZb4iR670ypQeO7aXh+V74pOXPvuRuhqpPo0IJwAwE9DRE+9t/lmvtUoP38jXOeCsj4vXhyUN3pPRL+WPxD/34GTHHlmbzJthv/QHoTva9FzYk8tH3+/iCf5iNSeGbhztUlLIeDm3/dbcTRtYNDKumNeRezrS4GP2NRD871U/y2eE0FQ6+dn5URujUjWGeI/y+I7vfMNXv7J7ctX5A+MnFB/XJT6eu+pR7XEw0Hd/zVe+Dn8hKFazsNrL3NdhxqAUV8A4N8I633E0b1RDE2Y86hlNvhOBRWy83KzMhmCX2SZPJiR2/y9H5XyxBCaqGlhaDls1IyVLlqY746PkxUeei6sBFfp6Hmt1/f9zj3SxHPGUWsep+DOlL3xRRxRy+v8vOPbgx8bz42ZZkuqEx+c2apNqxNnbBq7z/brejeNtkSD8yF0dt+LObzGE1iHSxf3jPi+voci6G+mzA9mzQ2LaOkBzpd7x7fdK1FhOI7f3Ev1h9Lgp97ZFvDRePfR6a71EoxzmLD5VNZ0341Bbmc2jKD8TtL5w2oHR5JUM25eyh+40gD8YDCgs4iqkm4sORpd23f5WR+D+mY8v/z53bNBj+O/VohoRr3mT588xkA67iNifA09ee7cp+wCLtbA3HXJ9HHemuhmUX0K9wuPq9UdeXKJp578jC1J7s7Gc4+eZZezsRrdXcduGets0P4okjwj20xUYurhg0cvcdxD1/hY1I3ViSpuB2/ZlcGtvwOp5bd0+QxdeeN4IkbM3RPbH336UsbFa1qMGDN9mbNmh2RDxHh2Yuu6OI7ZyFVHPNSbOADfZ/ra/fpFpv0t2lRNdnLkqfV3Yz5XYy2dfLZP8TLHtp9izM2DK6LZo/9cO9cA1f75tjzZiJjHYvC0fe+td8eXpT26Ex64dtbXDScuenxvlxfTZcnKJarp1HF236eaEuBEXWsPXYilHCOvwy4sfH5kfZLO8tAhFk0eCaHuHhQQabHlwBYfh4O2bTheLOQwa/Gux9f5mNbVoDCCZSfHBdpFJKj6mlelKW59BWM3dtURfLqWp92PqSYkLH++4kSSyfiwmQbNvDBmXsD5SVsWnRnhudiW+GNJ/Jv48W4iSn+EYXr4g4wFs80bzwkrXszfchPrFxhki+dkXZtyIME5YNVc/Os5u984jLZLuX7jUTnJa+z8Vdoxq0PvvapRHzNr2brulHpbhNWPjq8KeVWu6zbziF93dWlxYSXcO7riZlypqn3AvDl+BhhBSfTsPW8dfXsXXr+R7bX+gPa7NYevPipWMnGdeXK6k/rv1LL5jRHSX1/dOf7Yy1whpG/GFjaerozZeTWZ6OI5R7nszpUL4xfTSaf/7K8Cg0GslHKix6Bx5Kq4M1fDh6Sw34XO7tFYufNyjh44fyddBNGdWXIqiDpgUG1uoYr91LEqJZ8ehoSv/MA+GjvLsq15AQVGKk5UWJF4dXrg0ZulQkjdjNnYORHz8r5+/CDo42uhIm2Nw6lqKCVFNtbkllPsBy8jVD59eHXdqmTm0bAdFt9EjJVxbXEEw2+Rv3Pz6pWbc3PR+defRFCFc32fSMiVSJDMZLzVJB9rFLaN+TZOwqXlvY8WekycsASTeuTk5u4ZnM87hhhJLylJDRWyCvJLhWq6ejh4g2MSQnYFrnxZyofUHdjfOmGKzrfjyeYoYdQsjM0Mzcxce9rrL5s889jV5c5zHOuaDyJeWWFeOVbLjIJtNbQoqC7OLxQS9DQoeLjsVlYtSwhhu3jOM0XgG1ofQh6LKUQpi8tTK7EmOkQYozCFQTDTItTVPyIuPTe/qAJOMtFRJ3akeuRlh556qeS6bbZhi5YAXNt15lK9KVtPPFuxb7Bum5WSElrNxtq2R9P2kYBDZ/OleQqOUcEhBRIjSyFtPS0ysn0jBYzi1AohmaahIfmyZPEIa7lCsZjPqa1mSFNDYvHKCEjEZ9VwhBCqyziJZGNbtc34NZn5dJymtgamwc2SqDgiZTwOYhYnFfE19LXVUI3fAO/rnZO3INebwwxbRARXc9s29ozN2fBrE4Kn0n6bqvmHhVPMhzn073r59O2YyeY2dWVMWkuUvv34njBEWjoEzOznsZ9JTCGEqXz/7sG55LSh3q69K84Hbw64q63j1q+XTdTZTdtI7ueX963LeMmnd2sNHWScv/f0GpbW2XsDqMXRWz2Cc4fNGNntxZEpa7CW4bPt+OUxMVF3k6O5FKcF2IwNq3ec1xy9brhyGYKM/22+mt8czvuw+X1vqSzfsC591+a3TS7A1QfcPjsILi2Sool6pUbrn51JndffEQ8RHIM2OcpuGeyjXmiw9/n9wqk9jOvEQFj8OmxPkfX83tmH89tKleQYcKU+Dlf9gtGznr/NnGJprVBQFBqpKFFWUpjrgptk343n83dO+NrifrhWr8kHZ5m1150g9Ju/uZ/s0zRXjYwxe268LQy0MG6slfkVCZejSt3mNhdOYcWd8EtZ1iOGZt9Ib7DlzYEJLncqGu7Aj9tz+WJ3+V0fUeXrVSc/08YfvzDdHAcJB6jmddl97liG105tyUUYgvt+ztR9odmS4kwZvmTf+WEGOE7S2oAFR1R8L60tmL7lSxOHKTjfjicVg9AYNrRbQODr6JLpjvqw0k/nJgaeesrDY2vpMKsJFwKnDaxrb4sYsbeD/Y5GfmHLQqkNfHByVX9CzbXlw30TZOKNc7t/efNAaZ+Tm3B6xoDkns6512+UkqatnVxxOPhmJXlG8Jnj3Xj39i+fcDOVDkfBhTwh0T5w25a1Vvi2Z/64ec8u5OI959qotb4PrTvKS3/jqQdPqgZOpnZuApH+abfJ0shyySfLP5/98dY3+EUBBDkEXHrrg3mo0EhRdcrtgG1HzmXXe8F/96lgeLDRksjKukgDx5Bkvhi588rVnoSKZ39qbk4QNjlTn7aw6un5rb7hMUXSA4LbxLUXpvTSQkCM+L1dVpasX6B9KOhesiSYSq9DBzfP1ZcVHl7etahcosNcF1U5XjDr+4fFqZNnPlb5D+ikF/69/LhwikSqDj5eYdsOfJwVBpNUdwqnQ5QQKElqmoNXnphpJnIqv7PgDnH04aM+WnTj1Nvr46ILuH1l7VtI7Y8jy2c5wzxRKVO33n5f2Nf64rnXCK99+8bYwm2KL8+Kupjpb09GISFhueac+IPjTUsjHIrxA5dNWaKgUgD8K8F0Hbwwcqi1GyFhQstLMHh98YKh8MpoCI1HtihuYqFAKGnKGqs2ZF92anDoWzWfIO/K9W0LZ9M4eCIIqaZNbasItGGk/ERxhoNDgob2sSW83NwxM9q2UcSXPKe2FrHdWZDa1Cur36rO29urZEOjcOKcF15kzpN2WgQld9z8T7URvCYl+jlHc767oUyL4TqOXtZQUFRSlVAinDBhUsQp7LCgfB+VW1vmzTty/C/XLSNJhtMW7JtlbUtK2NQsIoyC8217si1geE0TDSj1SzlfgH46aeVZ+vgDJZOsVGo+rgpYOumA5df1LjQYP+POWpd9ac5Tdt8a46AvLH7zhWEufRLV8QefjoeEebdnGRxpGqe4JvmNysrTtx7N9Q27O3Pd2fNnZqx5ncuyM7F0GnNxhPMf+nhx5fs/A5YG7n848fBIo7ZyiKgi9X0GwnSTudxxYJRhD2eD8PuPczmTqZ0bfiU6rit7tuz1von94l4EXBLN231+qgHExqkj4EJFRvIKbo+YHxRnNfWvbWP6qQuzv3yp0scRCSvyHiwTVT1y9z2oHngxooeyrCaWdgvV+h0S9IOEpbedxhxukjI/897GwSfLJgVe2NMLF39104DjG+cYX7jhQZFcUxJk7jmLXnj43lzyu/FTNm29luK3xFoSo6gm5VEhwmGaBUnes6A1e3hrhJ38mFs7gPrdw+X/Mn5cOMVCkbLtfFfUsNsfynzgcAXjT1KUpP1Rmr40B3EJagQIo6MuHR5Bq9KIUHpF45S7mpmRdFxKy60rcdP75JxK5Ue5QtUeZU9fvYJYQqS4MrGMB1GkUVl5uZqiIATZrCeFefJI+Dj9uUNpYJ71PwNOx9FN8oep+A5hRfSdNxUqPX0a1oKKuIzSiqK4tzdXH81xnBgynFInqIKcx8cO1zifGmmMDWs3WRGHUVVYlHb/1vEVOeargl0022wDKzZSQaIYnX62ip5KWPLhynqUqZW54/AeRm2tMhRxq6sqstLeHAk9mmQ+8bGLtJ0uqPgYeu9TiRDiF2UwhMzrESdSURBMucuk4S6GsOKI4zcqe61eYIxe2yQaGBKjLCsQQjSizacUVBYUMSCyBbW+WwtXpmqioC/FdOmUrAhiKA854GunjYImjHFeF/P2WjprZHe8iaP0Oekto8IoON+Br1sBcDQOA/GZPF7Oi+uP4S53R1pJF+Co2swfbbL34L23tS5DUZmhF+JgTmtPT3LSlnpVx6Vn21GK2Ag7fwc19Ec0K637hK4UOg3LqWYLJTrn/Idh3S1ka98+GsGR2UV8qE3h5BVkVYhIffQVzELjaMbaED29QuLItoRTXHrZqf/lus9I4xlxRyd1rR8FEbNzEg0Dz63oQW74BuEKjOQm3L34BOZ0bvWkAbLpYBObOi/AcVhIxJK0PZUQSLQytr2Ja17e+StxyD5bN7vqSLqxzqPmzr87Peh+QoVHX8kjCoU1KkPnzTMnoCCH0Uaw29llHAiSCCenLLtIRB6mrsALGFo3KlRRUC7pCAPhbEQsFON6DB2gtuh2lBcF0YZwylCCyTKAkvQ/WN3NsLpT4uZ3wFTIOIjHoLOrKgVQRuTJP19J71bSNdJB16eBI2Kl5uO67dm1sOTPkGGzSg/tWTPbGPe7jAb8n8NLvr3V7wnfa9k0j/rSxnpzaHKfW7KxR02PA7106+cmmQnbTyQYjw0bTIa9azdW1pclfvOOyOIw8ljorfu9qzU7lagUpJaZvVNxxbtnZ/eeOrjUfnbUNl87BZUY88vBrvNvFUo/ao5b6Gwqs1HIKoz5FJclgISMCiHES/wcV46AYKqowUNcyF/OrU/QXhraSx3WcnS4Y4j5kp6tpH/bODeshJRUjWJx/bGuk1PdiDiGrE2F2MXMticofzJCLpMtSRnLz0ouEjBTBwyObnKxK50PiXgZz4qhrpPtNTs8TYOmmRmioWKYEpZmooeGvkgbJtLdGhJJzfoUdSIqNr6kLCu9GII1+kARIk4tD0LhMIoqHQQGj4QqeQK5W0G+QR5waftYS1krB4ammDSdO8DaTrEnNwsr10gRI+FTEWQw2f0HF69yCl4XQbqDDeqXB6M1umsjuaX5FXxIOmwP0bzsNWTWwTEomJhT7x0Rj8mBJHlGoReUsUiIweO344X/ED9DOMXSEZoBM7VuhsXhkTJRq1M2kaidTKcwRtn/uGw+hFRWRqEQELzP/MOPPb4t+xKW1P2tF16CycjLR8hzl26Yt+5MjxOzHb9/6TrgX4Ko8uMxn+AP1MHbzgzSaqhGcN1nhBVM4pZmvg7avz9gEVP59I4pGuKUe0dPi/rdGKqPhjjtR4wz3xZ6fQ23KuF1xIIDIe4M7Jcdg/Q7XQr4nUsUkq4G8vlzn4/0Ey/jQaDj9mMzbvd5PVZP7uwq3nxm7LXJrKrMu5dDFoUsrMKcuTtIA63rfTLIW3KVHrPRYGXp+m0HfOsKBD836OgDoefWWfqoDtrS2jgVEk4JYhYx+BBFVnnzmSVsiKKpipZ1HckaqvUzyXyeRCVIClXiVyCqzkkpUtLooYkSSyoG/RlfwidZNh9XEhaxudIRZWGHqxslOIYgWwwBw6pgv0UmKLu+N2DCG7WJI7zG9yIznhXMjG03KhhaGSnm0GsVtCWkC3AEcIKyQkmpNwihYmhgbC2v4lIiGeo3XXWkyEgxj8mXjqUKvrPS/WayxI9ikejbsjZJBQ9H1veIlAh68lZMwVDKkoJQwVHoBQZLgMDi/9aM82v5WZsvkdpjfEw27Y/nQqaQdHSFgJM07mtYQkhVyGaw6tS1fWQ3MUskrRt1eG1aRpUSzdSApGtLFt6Ly2Z42LbRzUdpuO+cee/c+thPDAgI538dVtb1sauvlDove72wT9M9cCgCRYsAaamNOrw8J3rBreOxVX7uRcERSQIc4XTIltNCXsmXKlHVw4WbCgf5LVhoIh1bYjHYcGU8+luJRapSqKoQVXvUkvCcWNfbt6OrBk1Vq7vETn1+7XA8vN/IEc03urS2L6nNRNsGZew6ZvSxF+c/5dbWCaeQU82GqeCb1K1IggaVAFHVFixekRQbcOxObMmAwdoKKh1m0pW9yUKCyl8Ltv4l4FW9qRKXPNzvW9Bz3YLRNm3Y0ixRGFG/qy50/VEKfbmBdFi48uvTOKHmbEsyHMqRXkbULfrj532OzVXSX6rf7j6VziHkMJgwAlFuI4KXe+5aImS5oB8FxzWiQC/jP9eILCnNfAHHaxpgoai3X8u81TU6VjUr1be5lRo+SOFk3Vj+F3/GwZ37rXCQoPDoRWmjob16C6WtT1aqykipFfWWN9TFLkrOFVPGqjfJTq2/7jaBo/FNI1ZoJJxgoIGFPrx7Vz1Ej9IybpgSAgnxGbxWO1Bbg6RakKB3X3PpIn3pcid2/qs8AdXWpH57k1JDXmgOhqqvAVV9zq0VWcvzArfofYlY04P2k/PNP8lPe2sBXMd5pOeBdTf5siOslj0VOvYo+l0vp/hr76ohBKcjW6jFIuk3m3Nr9/PeK3H3dyZAPRd218GTpnhohN44uMV506quUFoO18TSsNnmYE7+4ySBlaH48dtsLtHB6Df6cn5vBPSsD7lMITenTCBprGa9SxAQyIZ22nhx+bN5f+6PwrrsHUDL/Pg6VShCUCy9LMhNsypCmYiTtsZEEEK1p8cARpWsqQtHSKfYlRAYFFI68iEoCJkzfhG0IOPIKCM5pRmuQsQ0HZ8UlT+ZtuH4SxF0NEuzYG9fShtGqrWRKP1LSm61iJtULYB4FYlfE/g4ctcu2sSm42f8mmIWRKJJlUJQcKWn7wEo4NLbUVrybFSmYqSP2bTCgyHxNDIH01B9IVUtx/ZnlcpsQcClsx8wBAqDbGtSs3WiOKP+/vqXN4UeOWs0dyDi09rDL/j2S2YYoyHZ8kwOvbqGr8pIuDLnZCrFc+toaSUqqMhKSWaK2DnVPIhXlPX1lRCnYdDFGC9WcB6u4OvGZF+ZbXIQCrkYtkDrm4VibnVeSX5lUcKVcwd3ZnYJPNzfCIHkuQzpGX5w8b4bBouHOKkKitI+3MvV9v3DGK9sPcuNdOPBXv9z6L2DrTV4+a8SKrv27W2MEtQy2XyxmMGV9JqELBajGoJjcW2MZCopiZkpaQVVRoSYS7u2F0nurM8dAjaTKRBzOJL6ScyTbuoQKCGxRIzEDzCKqaORKCIivtrfk9zK59y0t28L8FZeOhhFnlf8JXHo7NpaifUiHqOWUY1Cq+DqtFaRkcq9h/ZVf/HXnO1ncfO8e5O5aQmJxYZ9h9S98w9DMycKr0e/zejhLM5MLtOw7UVF1j2UiMUVicUCLquaIZ1OJmCNxrmp7796ZO0T7S3d0TEXgw+X6S8b2VXSaWEoNhamYtZPS7T3cXzZQE/1Vg/GyX/zVzne2VH3Z29P/Qf5ea/7gZEcAvqq3oyUHWBN50/udSkotPe48w4DPa3gT2r5HWjsiHksPqLLkD9KD/qbV0I6fZffGKwtMbDX9F1h9HWLVo7bJblHZ8Tz0EXOTQJxCp+tXX7sDU+ScywWrZ3hBpbW/keoitnda0ti/UHUDo8oiNo/OHO1vSD53qUyyakXS9e/qLuI6bm1cKcLScTnQUhp5cHJvXT6Vjq2xyoHCgyF8Ju/2q8+FtaTbbHRyZ47V040R0JQTeajbMhhjnPTlyGI+HwIKV2ky8qN3ny7AN99Yj9y/SUYTr+3IeJlBszGWrux9aXISIWJVr+YOXfz64YAUxdHQcQBjy+tdsc1vPCMV3Ln1NF7fNPNQ02VJX27zPdfINPdzrSmNvL4EEpqIyfl8emjBdj+ExybrmAi2C1LufrtEK03MGj1wAZbPvp/jH3vOfvEBP029mzWtE4U3WXF1nXFG3b7T5cUYLi+88yo1d7SRTFwrJY67sbJWeSTks4Vre/wTW+mucj2STMf7p4zoWG/yYWdiy5ARL99EafseQrO4xR40iThQ7aS6RxvWnMT8067+Z6G42lWFl6hh6dNlW3hQen5RGyu9t8d4jwiRPaFUXoNWTjQwxiPIHgtDAqHb18WvtIqXHpFWX/AKfuexqhXw4evi6ofPkwbNWawpPpYf+KYjwK3YAwGr/d8NDl4GjkY0nb0C57I9j0tlIVm3NvoM/xt/bt9ji8dcRyCiH13Zwc6qUpC6fUdr3N2z53XeW7eLcf82RnnIgtpLn82vq5HjucVQP+0y3BpVJX0Y7jjsHDIOCDj+GjJN6LYSBjJcWHkcviUw+He/jIvYPT9VtkP0qZKvy6c5VL/3veDt5o8lxxQR204fskDdXvNsJGx9d6JWz+aBEFd/E7GTzV2mrLlQEXgkk3+kseEkW2Xb928zqy9cRS03ihPna0Rt++Wuk3TaOmFz5GRGaoux7r+LguDpPyYcKr23Ex/3HiE91h5W1z/rkaU2bCdxV4VZRBRA4eAVv4pO+kd88y77jLa0D/5mX99MOulBc+Wyj4arDzzWBrB4omlDBhVtWFIHGswbe3ZKctrSmphFKJsjAM3/MOz4XUXMUYTXj8YUVbNVyGpoH+fMfTfHzWvw2IveRf67GI/k3OaHrvDdMUbrA5JWJKXD7dYvH7lZM22sm9t7ofPSjYbnJu+Q4cZvcN38Fu0CUmUm1eGsBh9cVX/b6+KxHXdEXZvaY0SRfXbXIxCIxWh6vXqmZwAorL7ff0OZJFI4or8AqHx9JUbl0p3ZrKTP6TDuk0Z0szG2KkTlt9D66iLSlLK4E6jN5zs3+ZzdgCxSCCUdIrrn0peopKn1/U6dsIzpLqsGkXVaOyW4Wz2n3qwX8StYggJRFyTAKq+h5/7ykkKp+C8Ak+yE6LSlVz8ezeRHMLgTfc4POlkKgHT4rmRer1nPu49lVFWVCQi6qmpNH5PMJzx1OVhU5dySsvpEIFMxdVtYHKLfPxcjinGF+vW9lICIspkH/quvCHbswhNWn9pxPzSchhJV5oHpo0aWW/SsJ1RCsds0UZzZ7ge3BC++bPbcYemr3sVZEcfO1JptWNCt4Y35sj1PNYp4KoooGWsRMf1lc/Wy0kOqaXASKkXrAcv/zB4KauqvBwiaBBxTYaDURY+2/MGVhdUC4kUElHmnhFBT+Q/FN5s/sYLc1ZU5LOwOpRvPXSC/ZryJ403qfjsfdxkShNt7TNzxI31605/HvGnA6mpF4qiVt2s7D1rostv1aX5lS+YheMoGt8bktbqBVAwlIqmolY0HKtGAUO0vzkY/aEHFpkklQuouubuPe0tCa3H3FDm3gtP9DGUra7kpr35ALktGNXsPaEo86GLDnbJKRAQTc3sB9sbtNwTAsOqdfrNY00TbcN6syWzJn2uEFJ1u/Tp7mhTtwOVm38vFhq5oK9+Mxv1Zi1cbJtTxlfVdbTr5WEg5zkV26I3fcHKYYaUFsWaW5lfISboqyAVJloPDKOqLqfMwtCkX/O2NE7+myjILaRv85e5whBoDELxJDOCoKYrv/MCx9AU7YjoKHBlsmYnf2ECrtl79lYb/3k7jww/utSbXP8ovKKoxUfjDcYdnarbsPyoLc//RCPhOJK6ntwLGFW9DtfIcCylU3PZcErvndNtugXvWOFy7Ihzgxf4RRcOHn2pMf7NILmvl/zvAt7MDviPgKbZjBlq0+YtCM1u/fzrP8M1+66J1jBrviMbpWvjMbPtODpN00QVAiMYDx9mPLzFWThl9OpgA7PmKoBSd/EY6vKdtlD79BtU91FQ+nRhUKyjv/9ozfKTZ6MK1Ad666AVJvoPgaC4n96n4fivsOUHQOrMXLc2Zs563+1d47cPlo5hcDP2btz71Gz+q4lm3xTu3+T5XwDSZMj6s0mzR23a1vPkjqnSURJuQsTGOZ/Mgg5NdPjd+jVAOAG/Jwj1Lpbq/7QR7YAg21qS27/tOyMn0IRv58y6NVVasfcNCfSvf6/vL020kyDIXZz+Lbb8EAi1vof3bnQu7aZTV6MiaV4jFvftNcCyacf53+T5XwJCbeSSoAir0j5q9V7QdRxx0LaXXwd+SOG/BhBOAOB3BEF22LD7yjpOdQkXq04Es/+/HJy+x0z9hgMYwbH/oH/Smn8KjP6Yod+8oGref8o/ac2vAwgnAPD7AsOoduw3yQAAQMcBwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCcAwgkAAAAAQCf4GcIpYJUkZVfCaQbmVCx4JSYA8HvBz7izwedZr9s7hhj8H7ezeQV3xq59Nmjbjhk/+uuogN+AH8wDgvJ74RsnXYiX/VK53vrw8EAThS/CF1a8mL/xCnripiAnVaCvABmsp7v8/oimBp88Mlfrb045bob/kovUBfH7fYzaKAXctA2z5wThAhI2KU+fuC1v0P6PAVad/L1GKYzPB/rtK120e+N4NTk/xsiI22W9NEor4NRzH612SyQnLbzH3MsqAaeu4Haaby+dGhK+z0rujzaxXhxYPLd09ION/bTl/QBkhxNFqutTyj5cjcgfsMIA2daNv4qfkEk65WG5oEj6mtXv9z/O95tg8I/8tOSPPwLg5/FD34Cw+EXwxAu5HouO7O+nQc8qUNaTqCY3+82NQ+ld10+ybvG7c2Ieo7i0DFXLV/hb6oD/O5QwGBGfI8b//b87pITCiYS1Yiyu7SIAQyuLeLUQFodEI/kCARpVp0GspCPdF1z8ypN8hKuqGf8xbFbw+O5tdEWE7NLkrMJKgYJEUGihkCPGojtSHGForIjHhrAYNBrBFQixKEWtUCGzNOdLUQ1fUTwdThRvNniy+q3QqOyF07v8E2+M/wmZpFMelg/ObGp/9aN3o76Omm77T/xM1k94BMBP44e+BFZs9Ptqnf+xd+aBUHXvA79zZx8zZhiMnVApZKtEKSVKVKIFpai02Nr3Uoo2LZTSQqv2TWnXpnrbd9GCbNnXMTNmv/ObGRQydt93+d2PP8w9596zn/Oc85zn3OuxwdlIAwNo9KNK3ISVN+P278JvWOn9R1RqY66c+3/5qR0YmSCJ8lgAQ5L/38/hkXgqFsCR5FoZA5EEJRwCTyKgQZwiFiCQcLViSiTk0nlU3w3blqgz394/PD92DUP5ZOJoWnNLu9ZB4ckE8ZJGrk2lgCKQCQisAh6FxMkTAJwCroPqm3ZEitXzdtaOuHrzw9QFg9r6RWL216RjIddffazC97WasMXXwfDXgxDjVUL0ivvsScvW+rdp8dYFjaRdJSwDrImjc+8zV49mTI0y6orvMkOM5CPh695zeruvihlBa3Uk7ooswHQVnRKcCIx4/s0oKOACJrW1KSiM37Fpxw8AAmOdA64PmhWyuPLg3Je9V9iURycUei6yfxR1AeGxfo8l78Ku7Td6TbbLvbjvVTHJwitmvmNvyVQWqky7tCDmRirWfO4o5LUH2NXr/GxwNSl3Di69+DoboTHBb1W4lWLHxiaYfyRIIpmAxMoTEU09IF51bl5BFZbWS02BUFvlAjadI5IjEhA1peklkIYWjfS7KUAcenF6YTVKUaOnCrG2UQt5NUwhRk5U9r0Cb6BJBhkF3xik3uqkuiYvFpx4kEBqbVcexJAJGDl5sZjCUvEovHzDBSpaSU3bqDfOSNv/5f2A0y+ymaNp5DovfkXBzzKsmgG1gVhDSDIpbCbx4jFRnghiFfHNlEJFcd4PJlZbS00Fh6xPkZw8BkclIFEYeTkUlkpoqUNIQxQySn/mQcq9aY1ulRFpMyUJABhD+3HmR08e/uI3yILw605uDYstFmgEbF2w4gpii7AEAg7JSTm7fPCBghHTpi7GfY85umlAJufj1rF6aEBIT4naHrryaQkfoFmyoT/SK6gq+lkgJGmrUom/0yqzkTR+lENnQzg5Qu2nRwVsJkuEI9dXV3tKWMBickQ4IhFRk/+zRKispV1fbFjtkXN7Hg2//iXMyIL0O4Caai6Ak+QaqH+cDaEJJOzvDAgYRd/LhYoqqqoNaoCbk7Dw1LMPEFBuw5EUhJDHYAvxOFH+zwqihiYVwcjKY1C01BXq60BmFmD+BjolOImD3JwN7p/z3Wp4Y9UEcyIIIIhGAwdbvf6chTabOLJPLxUML/3LnXvPXt/nq1m5K4vKX759gxjJhwB+0deXx2+nvrIZO9msKiJh2/zepkljaKLCm1MW7X3Va/xCvcIt259lI4fMEwLMtNhxW5N6TJwxn1iFVsTDUvO/BVLbZU+5A0gkNnTk/7i7Y3zErc8IsqKQXkF2fhi/wo4AVL3Z3COEER6svn/X9VQhACgOidkdMk8XJ6x4Frx80/50FhoD8nmQsvnMq2HTrYn8lON+o78Ossm9fKVEYdba6eX7IxMqFP0iTxwyl0aGpPntuT4NxJObT9gv5MdvvuII4klYYPuJawI0oRlBK2CWcQAlTUXp4lVY8j5++sa4OxWSC0XTaSdDZo5RknYzEMl+vdM0slHi60qBNjY5URxJo1LgFdydt3r70SyEMklYyiDPijwVay4VWvJDrl4eiMQTcMD8tKtCbHMp+gWI5N7d5Rt4PZsPAGpDFt9f59qnXtn6Z6QySlISPkp12Py+MUsTPkRY2CjWZzvz2jLzmMp5e+KiTImAoPjkOh+f3HFPD8+34jxbdfSjiueh07MNCYBwNCWvZ0T8wUyHbbpZa4OCY+S9zq7Nnx2W2iihEOPttcgZB5JS2dJLZafbR1eNqpNOzTaSpjA+7dRf8iP09KEANfEgUZ241nUiZ03JPntqe0uY8WaGx7rK2cF6Cbtis8VVRXVdvPvUeF2CtBTcXPsu338leb6Fi3xdIPyCq06zYorH73kfbEYGBLl31vbbkjs3OnabsfgJqOrbtaDNMfHZdbnyiTh2dKA0V8LyxLizWSZu47KvZEj9OD+ODVj21ck4d9+TEpUx69ZU7wt6WqHqEpW6zJwsOwswfxOd05eTjGddW17iuD1qYFDO2S2B7qok82H2tqcPnsf3950wggoIczAokZDeY/6xpx666LLrdY8h0BIBqDD6yOr5gxBp1S/mHXubxxyj8DPpXJLQ4uT6RdMUKw2zPTxT0SiEoCj1XQ7R6pDvFAe4wfwXAdEEchOLE/rzhTtv0cfsLgu2pCK4pZU88q9FjiAj/Ihw7s5LAfJPpwXuXn7ohVuYnQpR12ny+iCbAYZEUfHrGNulR4PvOD53Fw+Youqvz+VXHr96198r9vqcdSdPnfBb8yy3xryvNDwQQyC2Re2FwhNrB3AcoUkT5JfkZbysKb53OeYqbsTRsT1wkrH4useKo/mOG9P9rUk/LnotPeixy+B72AixFyjM3nUcM69J4sG6UiASm5bCjb07jjKd710LticjOFUVbLlfpYCSq1sKYkmtdApQkHN+I3b83YsTqE83DYmMWfVy2OVhCmB90TeJFNl8SUpNUZDKLhPMg7dfuVcxaLJibQCYvm4rw5NnLtt+0uOwn/bzPQueKyzaO8NaPMX5eP8xRy1weA9pipGa/R1MgF33vlQKDXvMCt4918RMIWVjk5LMTFxruzvdxjfi6mRLHWHR81SGIeG3dzONpL20r4QFH08eEYzb9XOC/NWwgICYQ7eGhrlLig2pae1mF7Vt/5uKMSPqSgGr6x7nl2wesz18ROxm2vOFe56rTI5eK5GaAC//mlvgrvfGM29tnjySJsxOTa3UqYuC9f3C6heUgJ3WxevrBKcYEevrDcKqlPA7gzcdjhsbkrb2xIDYv75xzAfiZGUB5u+isxvNuD7O616QyY5rEyYuAu8fDB7R2OIQIWlcPabZaoon4w30MgiJ1kqxh5bElaJDAhjlTCFQ8/ndT0DLZRAFBEC5nvqKQCoSBaBohkZqzJvLjtgnzh+iBTeb/wdAfGY5F2DTy+kCgIrFKlN/70JCwmrS2IUrzJWxgMNim9jbL5I/1tg5ENVdHOusLWkmI11VL5zKEQcgFpwQG2XuY6mMfYetSR8w1YhKV8FzqtjCLktp+YkdSy/wa2qECAO7XhpYcZvmfU+68BA1JGH2UAPxQtB44g63RIvzN59Wjxgpaf9seZc/Ey+zFOh0LsCrKmIJADIWR1HqkFWOOE6C3wIvO2UM4DDFJe7VreQMxrABMhfZmGZLstaGE1Qd4DYaGbLvRan7mPqtXIxu0Io5l2fFzDqA7/3oqYJ71FojsWAQVOQXMgDFPkp1FYeUU1LDAKlF4vyoGfQ3E7vQm8TL/XH49HvQau1xbyupAbCm7aCO5LZ9tFDCkLCcMC7ay1wDA0ydbLPu1YtLGTXuAyRVBVIHBFohJ115kT9sjFZ9KYgnEJsfz1y+PYao9egqyf2ht5F0psVNuX7mIWgVv9p7tNSU2sC0PleConOHrlRYrw7Wx65tkCIhD2XnZKmJfovnpDs4GKmxlOV4VYw/9dkwfz9dYKGF0hiy4MFmvuWqKyvvTno24U9lKo6Kby4aBLJuti1V2ouE7DKx9MQryEvuRYD1mnySScDNBZWjo1ZblSy6vXp8vxYVUzD/AUDFIVum9ZtwMkz/+TEHR7eV08aOoP2SnSpOVhrSCwxNgwywK6qkYhBiFyTfv3n6TWZOWeHHIgAJiWott7EqvXtggSIQgVcx0MYCqeK2IwC6biBSXRp1YrshWPjp8sxV+8eEU79ttc74XAioOPch1q1GdAw1sfziDDp/pOzEyyqFcXO9bdecmOb5fGP/UQFTp82xoHVEdioPGq0hXVdjFA3IAKOCKcOwtw5ZJSmBbOZvi3e68jTH0f3XAR6srlus30OzmCNflCc89OknPWcm4vPFGRNBv55EoEkYQCSSaU0PMTOTiwCj6RZqXbYTIxIKWzPeb7GEtays9KXFhlPUUALYRcxfVUUe5mpLXH45odgx6NepEIxu4HK/CzNj1ueoBET6DiFJax9ipHwoBHSnD6c2zRU9JT4kRWPJYWsamNbIA61iqYYFKpAgVsVM3OazxKNgV7ZXmK6ja0ybkTSL8VNVbxz8lMecoNuMf1v2sxFoyUY+j8ESN1Ek8LvXgQRTt9AXCrscNux2P9nn49yGKhyY/yKg/NDZe3LHvI67cPngrT32164E747ZbVG7p0TSpdQ2WYjHFQAYkhwICEqT5wVvuq7kGOgw0lmx5lJ+xP26gBBIHElqYwLi5fHdpq3AqPVzDRt3pf/Vp59qrCFxwxU1kBkScYHEIBGyEi8bUNF09qMLY+7eOB997daCRVf3u+9+Fmip2M55I0JeVbkuTj5bAOBJuBZkk+ySrIVoPdZeOTDh7M9xq38d6IQ4RYUVkhMvzJ8ZTKGdRGYg5RUICIBZyOADVOltfGYxG6CqUWQZMIt4bK5Eld2qrGszAmYeXQi1MlLIKGGpn6IqpVaNL+TzeACmoeky2WicBzngwP2fc71/2QRDrIrCIolsZaTnMwTmJIw0V0xxuSAEgia54ufGHbgttA+fq4MBOI18ECCu1ooDxMoTYWuOfzRddSZIIOkbRAU5NAKJAcWzTWG7FWKgXO/eSsC9j2k17j1IvNJCRgM/tM7weVtu3J30Nr0SMoTXnP8PAOXUrYIXWPl73Bw9bevxq19CLaxq3VFS21SAX/L4XTGo49EHz/18NuYo3+XJtoU2BEBQmBAh0QPWjVWIuikbAtGmuVuHEVSW1wBYkhwSraCjAKSlfmVBhpLFFzv9cy6PbG6miAJ+/pn4KYatHWoA8eqjJy4c7ep5bNlU39tXX/lajia18sgfQSBrlTe8ko8PihGGU3Rk74pyPyfILMla5Ho5T1dNiL2btXhOL+niDCp/c2BGAnvS8tW4w5sX7rg1fOs4fTRI1jHSAi7f/UZfrqskLoWKtEfvhWrz+sq0h0cS1XTxwL0XaaUuNNUO924EEinis3jiBRpSWP7hag4A9Gn9oWZKuNa9vqryPr7NRegs1W1QVfheM0er7r9+N3XyHHPpXACiv165OYFpt+I45tCMvTuOmW+bo4EGkCRdVTzw5uXLqrHa1N+5Yn65sPOrkCR/Kzj8loBX+bxSVHxnj1f+oOXOdVtYQPe3V5hO0ynByfl8+9obBSMzecaTy1EnGXrrnHvKgXwaFStK/et2psUEHUp7QsObjXbQTzi77NANqF9u+F9MQDqdq/n59pVAz0j07lY2X8lSnQhLzf88nJzLT4r6WFn0IQoLfuaX8gENXcn+k3R2zqusZvMorKcXdm74Lu8RZqeNAlIQCIiZ9z6fYUJK27EtPgvZUEvYHgT5UfM9FwLBmTETW3qXUIMHKsvLCksE356fCUhimvm49SfgRSOG6Vy6uCL2ocHsAfgvZ4ISSvtOcR9EAHjSxJdX1fAoNfWJH67TUiycr8mPc3QGDdclCsp/ZlTxAaUe6i3YMslIvIhXXVrDV675FLnryFt5+yt2LZ4XbLUksT28nbW3J9x8593LBg9AVS+Xb73OGLxu5+gRaOLzGyF75960vDleg6A3ykfn/MbDMSf1/J1QH9buf8K3WOynLxYygvKsb1+ZEDunigfwCrPS/hISVHV76suZzB2mcOX2Tp947E5nE1Xez79SKozsBuvLzK8g88I8g2gg6kxscP27hLBKumqiO5ee5fpTEediTmUpolvTMcgoYWlVcRnVTD6FnnJh/tHvVPvwiSoNiw1r7OhseDrhSLr3XmNJKdw+sPVwzZBTAaOnIOVuPA9ZtOOG/XZXfbTc4HF2tCe35m85SQhwGazITU/5XNTDzpHSd8qomhLpwgIlndWAKAwOjYIHtn8VnRGcQvqnv876Pi4DpFqPhSErV0qmoZjBE8f0fnZlxszPH2KOL2xPeIQ+My4G5nsd2zX9o/VMW+WXbzEokPsjOdbpUKp40CQbToqfY9ba4QGYfz2cwmfRUTEP6zQOcuajl53x1K8XnDnr5oxZJ25kSibz1u/fYitZxPR19vG8Gx442zkQUHKYEbyKE7pR2CHJWfPjbjZgOd9Gu62doix2tVeseManaOAyKyJyioFENdh35qUFFZ7RoSaJYjmkaOe5+dKM3mJ3IZ6qTXi8fp7zegDAKZv5hx7YZNviiWRu4fUrUcveh9VekXs6HV7v2a+FlzU0k3gkUYkm/+TIQJcj4gLTMnO9EDPbtaU4sW0oSUxv+/EWR48fTpttY8a7vn/bEVb/2KDhWkgkMNg/yuald/T2OMsd8zV7rghfV7Q+wmd2kjgZOjZz7q12kYpz5p2I+VPrz6Gc3rbwNECesfvcMQuSw4JdccgtS+NWGsdJvOR0Rh+zGKSvJCu1NSlvshG95ruoNEiZukPYuOuuB3xJB5D6IwI3mB6bWyQ7r4DsEpYKzrQ4P4o4JSilIePXP51j2+TFFlitkfN6Hd2UmBZmbMZ5tm/WTZbD8sDJKuJSGLIj2OZ2eLTfjf63XTUV+i9IWo703R/n4iPNFU5nxiqLMXZOu1Y71efjnc+7t6/t5x2ZqgOlH2oxuTD/KDojOJE0r02XPTjVJVyMCvnXJgCoaLko7e7MYjZGhYJH9o0Vja/3UHJ5lexS+3vWwcez6lzVg+IeB9XdQjCbFJY2CZC8nXKbxy4cmQhijafGMN2qSvkEFXmZ7xaD+S+B6+H54Jp7ZXlJIQuprEpTbvRmHIPdRyO8VORVGtjlY9RGnT4zdHcJHVRQkdw80662OZn5nWFKf1CDzpVKf9itvFIoO15W7puPCNP1Nq2/w0WMnHFwzr35XL4QQuGIDRsmSLR02/B9/IqiUpacstKvtxyQTBem3FoIcRmVYhHaylv+pGB7LI1MDGKU55WzUBRVbUor7wdqLvEE2wXH6QsgDoMhwJOJbYhTVkk2BKU6dL7R/sUJH3daDh63OkG0+pcHbdqW29N+xa3lcPCIfVRVaRVGqcGpf4rX/sdezUUNEvRnLo+duYRTUkYHSIpKBHRL+WXn3MtA2PoMbrRkR1JdlpxgzizKF1J0lcRRuvu2nNsWS9gs8NitkSqKCjIOLKFUJ7gaLYu+8jjAcuyQNYXJa355aDlupTv+zpWJ8/I3zktqKsvKAJIqmdDCEIbrOSf9jvQXOejHNekP81X5V1rOA8zfRaf3OEGcvOof1n4glqzWmdc5cvLufaoi6PbRkYaMxFNUu+IVVzD/GkCMgrKmgvKfHgg0nqLyp+EEEk9T62QT4aY/fwMMC56o2karDBCJxhJkaQOReNXmmiyIJVHbkSTx7coGpGZK4Q9aSDyII7VHTdNqSSKVnd0Gbjj16Tt7cGuv3wNxFJpqO+IWB45TaYPtMOfn83vAsCi7P3ML4hTU9dsRn8wSRqDwygotGOggNQe5jTp66mkee2zrr99DEhRo2s36YLRnB68c34MKv37238Y/qcag8gfT1l3lqCkJcp4lFvcOWTOwLWMGDExXgFSzW3NftbfC352ODvG/TDyoOmJb3oj/RUyyQFGHH9+t2r+9dlJdCki1T7xo39lQUEpDRsKv7/438k8SnAC2x8Shhkk51WibOTc3Ojmp/x1fYoD5fwqK1rMv7e9OREf5Vye+3aAUe1optn4bDEy38U8SnCCxh5vHfLe/Oxkw/0wogzbRk//uRMD85yENunjr8d+dCJh/OP8kwQkDAwMDA/OPBxacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO2gc4IT4lTkVvDllWmKsj5MCAMjG27e/Z23MxiQ5JO/5k7ekzW7PAbe9wfnjqfXSGPo6TtlhEHzHyb+fwA3+8SZu1+4IgBAUAxdFg5T78wHc7sETvbt7Xdz2CLJ5x0GOE9yU/8n1A1UlXZxy3ezteN6kVr+dPj/DIjx8lL8O9MZc3sROpIiQdnNU5fpI308NTBtcodpE50TnNUfdpuuSA+MPR7es7YbCgufRk65gF4dGjia8g9pdzD/XNg/H2yLTx3oaK2DEVQLuiMGbsaDU5tT+3gPUsUJWTxRd0RR82j7DMf7SpFHY/zVm/pJBPbvK/aLQ0vm5Lnd2jBSo41fy+5git77+Sw+oxT8ac8EvV8dXCSoZlSV1vB+PL37sdRy3j9AcEICVkVVFZNfkHA346fFeJmCk/Nt44rQI4V88U+s+rjz27xNGyWd8zXpxM6vKn4+4wa2WdY1rpffcH/enLHiQLrTrpXtyUh3wsu4tdn5wE+fXdM6GkD522dnQ++ylfYFOlCQrbvDtIkuVtWKuIzyn6VoOr+ZIYpT+HzflQxrH28bQtdGCvMvBoEzCAha4SrfjTHIGbhFrrDttg84InA4iM8REZsIIvpz38DIGv/Yc9a/PrgsqinLTSus5ndXSn6lCEOAhCwRntCwd+MMAoOWi5N1/ucD/+5OQNsgGLhHSlL0IP3BrpbuQ2t4+C0ZzOVlJG6Zl1Iu0R40hJMVdzg+tphQ0d/+knUbvm3dTL3Uw887tCXygb7/q1lmCv+MaT8vL9En8l2/+QfDTDu6ACb0XrVx9We/jVN2m6WFDFNFtuYO0ya6WHCidJ02/3Bq1ktY/CJu6Xn8uaneXRslzH8SiJG2P/rAWc7ww2sm9OliZRK/8GNi+LkHT3PKhRQ9Zze/tcN1iR0fKJFEeSyAIck3TiQkqEzLq1TrljVuqynCU7EAjiTXjWtKiJF8JHzde05v91UxI2gtjCJQ+dPA8NOfuHWXGHWnA8vG9mpXhSKJvYwtewEc8iscIuUPX1zPxSsXUzKUPMzbIDVbqhdhweOYkC+ayw+P7fO3L8ZrEZZdPhD3UtPz3VhdXEN3iPEqIXrFffakZWv9dX8XJSsnaeORxDsZVXK6VgFzZnrp4GvdUbThu4KS+oTtDZtgGW1G/HW/LHeYNtDFghMqf7nH4zywNGThKFJNyp2DSy++zkZoTPBb7kePnXE2ExCB61b4xxrNOjuLcu3g/qg3hQiNoZtX+o1WhCc8ML8Qln++ODv0QEKJEKD1ZkKtP9DO4CvunL74Ws7WYzzx57Pz2zYuKiMdPzRQvqOiE0kkE5BYeSKi3kHAobP5QhZXKBLxOawqhtgJgcYT5RpoTelFOVl8ah8NChasfYLJlCppUDg5IlpYWZibJ1I2VK+XxRCvtCCvDK/em4pvlEhZ7mLBiQcJJHz3rZq4OQkLTz37AAHlNpyW60fEK3nx7ht/yEgr6ZIJpUzBIVp8oB1AvBpWjRDA97QP6IUi4pr6cquLvxcw8TStHgo4yfjScr3wsg8fe4oYunlej99is8V6gTj04vTCapSiRk8VIqr+AToHkiMSAGbRl0K+qo6GMuZ3JQjZ5Rn5dJQCVREDIgAkQY5Q7wlxqwq+VeH0tZXkGtQZNzsx9CngFu5q1ECQC+kpUdtDVz4t4QM0S/bvsq/JPOMccCDTwnvlFOy7hKNT5/5gHdnqp15re4LUGDpnibZv+JHkFbudtX6PtbLcYVqlq61quWVp994gvAQQMy123NakHhNnzCdWoRXxigoDx/Z9/VcReqidw0BN8qe4VTPvqS2Y7kquQqni4RqD+U3Nl9ihwQmKXhtO/dw2Na0bIkDSpm+O90FKhijIUTvPY93lO993DuxP7mhw2i57yh1AYv2Unf4xQm9xUkXtRehkBck/gvu2CxcHSdo5iKi5uXPGwpt5fACgDlr0dNMEQwzz0Q5PhyS62HfQsj3TXmwMfFIGAL2izhwIVkeUfIifFnrsEY+IZ9FB46mnQ2c5UcWdVijDvS6DfnuuTwPxHc1RawjLE+POZpm4jcu+ktGW+5FKzt6LtvZuKtk6TfWl5a5eKVLhQRh28/wmp19rTn5B/M5Vc25lIcgkAZ2hNCbq6wpzSGa9SB7j5iWfziXa+5sq/xZdMuslAPcqePmm/eksNAbk8yBl85lXw6ZbE0HGp509VxaHBGvs23XjqxAA5K33RW/y18EAguKEA6GzLmVgqJiyUuluPt70yMkoX2VQWPlhS9iG0Pc8BSyrFDReuS500yAlaUXyvj9O+kq03GHawFqE82VtUHCMvNfZtfmzw1J/lwRUcf3Q0WQFr9chs/vjAOFAyneviC3XMqfOM6zbFsNqTXTQ2XDs9sNKp+lKDYSzLHeYVuiu4yiCotR3OUSrQ75THOoGFDuPfmdWPsQ7OE2YLPdzV1wRxWrZhikDuqtvw/xrIfRwjto1bogZ6emm7ooCRNaNESCKSEYDODy6M3M3EE0gN7AqJ5utyLu9FKq8O9wrmhZ65txAOfHKBoURi40a8Q9+9uUdCh7PrrvSXob223Riz7cJ+02II9cmipakBHovevAkcodwwu14574AV56GEhTd9F55ku65t9jbWL763aqgJd57+6aF2CqW3GnWXaU+WxgCsftsJVnfL6x+QQnYaV28vm2Cs7ugeEY/8gSEedfm6sY08ih/vmfeLdbMXYlRlmQEt6qYJyeRjTLrBZCoyr6/zkT12mjYUN8rs16QQl2nyeuDbAYYEkXFr2Nslx4NvuP43F1iG4YQ/NhxErtg/w1/xZeevhvDL32bsbhvdXKkzxXe4v0Ja/tgS55uNQ/5MisqQiw1xcPkybAVm5mej69OtyZUPzwU6BgePehEyHgFEICq374uwPSaNaBhinA9ZgXvnmtippCysVGGWV/PfuTouQ03luYGqTzASw/wf5NWIjTUrWvZmB4DbXTjbj7I5UxXamhjIssdpmW6S3CiaIZGasyby47YJ84fotXksApKsb8RtfLm/pARWyOG0GBraJhG4DRHmon/Mbs/JmHR22s3quXH2Op15Q4PEkPAA1ANGhSPy2isHB7fwE8E8OTn+E/oT0IDlsNNwL/SSht68r58Vr9wcuooxVoBKMh8cvkB0va6u7HEVoViGjjJYGf0jRcsa6Pm3W3HtWmbr3MIis4dulJhvTpYH7u2jY8IK+5djAvt2WNAf9tReqTu1y9BXFY1G+CWVrD4ABmHpajVqjpbqhdeflY5pDBEp9lVcdN6EQel7uJYZ0JNMxnpqnrhVE45F5C4CIXV8uMCAgxJGMBykh54LbuUA7BTn32s1p7h1VNynkTVdMRg7J2bqRWhvdVFxU/2vke6bp1oLdFjU4a6TTI7Fx2Xyho/hATwSlPLIdoQVblGScEZ9Jf0DXrjBAoYBVlsgKajVJd8pJwGFQNkF5fxgXrBCRBU9DUAeoY4mUAjASnLHaZFuu0FCCSTgJsLKkdHrbYqWXR79fh+jStriH/E3oqlQWvm5S3ccWK8fidMM2BgOgg359r0LQ+5/ZeFWvwPBE49Kv1HqEonkkgMHhSxGlupEE2dRvwanQFO1tdCAfP7aOf7DW4xovNluXdruuugp8SHpGgsOWxNA9umRsco9bfom1OedvHluQ379tnP3X3Vq5dc6491BlB18JzV/daEhXncONbfe8LUVWMttVux94E4LB6AIeBkDESN60X6ALsg+f7N028yc8oKPxYBSEhUX5MqDhaq0sUAEocBRRyRZBecQhBV5fzkAAZEQEDPy+LgdVSIYolGL/yaLWS+WzbmTIOQrVnSioR4dB6AxWPaMs+ABDyBWL7/SgKAwBIwgAhq1LhQOCIaqOAJmh7FkeUO0xLd9+YgkGDqFvpCYZfDht3uJ/t8nNuzsadBYOgB2q7FkyPXhvU5utWwy/c/YGBaAqp+t2rt7iSyy9XVY/T+h6/vAEk0Jdmdjqan2nCGKRL/6filxnn3bZRCZlLz7t0PPzfuwG2hffhcHQzAadMTSOrQQ7uGSn7x8o9v9PM5tP3gkNjF2t2aSgCUN9sUddH39Y3Iy1eP7V10IMH9/v4FI1o68gRi5dAiDp0lbN67Sb0ISpPnBW+6ruQY6DDSWbHmUn7E7ykMgqRNblLBePPx05yTIievEs4wxnx5dPOH6dwTA6Spkcg6nfDjR1br/lGRIFoeDdRUc9pyvBklpyCe+tHLGTyAKpXZ/MpKNiCvptwgVIhfUy1AkuQwTaSjLHeYFuneV+6hdYbP23Lj7qS36ZVQLxQaAYiEgl+GYGjVSfPmjEoKuZ/BgAxlTfVgYBrBzLy+Nv4jxXHOWmvljjdeTlb0hlW7K20O7l8wjtp4Tl+TGRd38jHRcbO3jUYnegeIQKEBPoPX1OYUASJBmWalSDyxYUfAaupRgaefPlZDfakN+4cs947S5iwzv1zY+VVIkr8VHH5LwKt8XikqvrPHK3/QuuBJppKpL/v740v7PyFHuru5qP2xxMNouE+yW/kk6VEu0IrgFHKq2KA8sXNDOYjXs5q4x8p16a2lvbfePvBlwQgrqXPz9YLR0FFEVGZ+Y0GDm3k/T5N64X5OiDnKd3mybaENARAUJkRINKf1qzsEiEI0rWCsislQbfwrEAkBig6zomKHGdcqHfDKemrA06cZdEj3D8scjHIfRaA4I5cOmbSqkAPldKxVgOjX38o8ddXFN1enXUoX6o0zang6k134NVdEnUJrWi+y3GFapAsEJ68o+9srAUqiH6BoUetda36+fSXQMxK9u5XNV7JUJ4IgpEAlAKmJLzNHDKUxv6bze/SA3r1M45Pt1bvRbh7m34eAnvottwrifqkSALzyz2kpfIKiUU8NsmQUYH+6diTqQRnwFrQ7u8quY5sygrLLu5cteIuf4O+kVfDuRp5QiFS06t+39jQi68e19Rcf5ANvkWbnjph3YtcHp2JIFl6+/yJzoI3ox9dSVTNrJdkp4jCZLA4XEgl5NXQGA4+Vk0oNtL7t2EFx0Yt2X9FdNNaKIihMf3MjV8PLUV+We8d2atueZTSl75RRNSXSZRlKOgEAURgcGlXbf6Gyh7PWH3oKAQey1PJ32lH/eJxbXcEASNqUlhIjyL8wyGsvEHT2xUT1+mFBwGKy+SIeiw+JRHxWDaNKgMDgiQRUrbuIwRUv3IQ1YnexhCMQsEigJif5SrGOk7kuRVienl/FA5SMfhV+M/UiFmIgtVd/PejcuU9VPva/dbIy6kU81CEgZt77fIYJKW3HtvgsZFO1aBM4Px8eToEsl05c56RHaTDkYjSG+vWNWxS9e5/q4jl9Kfzy9KTnuQYjHU0IklWzZX914bkHT6qcPBqkqDzr21cmxM4RZ4pXmJX2l5CgqttTn6jv7aSz6/jhFXf1IqxQj2L3XRFY7B+r30CPx01/8SKfaOyg2US3J8sdpmW6QHCWHQkLPCL9RR2185lprSP3R3Ks06FUDgCQDSfFzzEji/uVySRfrWf7tvg++7Zu9rdtIak8AJAbOHHdZlP47C1MA5iv5vhvelZ3cW/monsAefSDs6uHS4Z0vMV49/6JB9/Qc3LZHbVmYH+Je1Ai/n9l/7ortS6YQQmXt4+XbnTK9Rwf1Pvaym/0L8UdjkAKoe8Sn8E3I8MNHosvlCauP3R2hKzQmI8iJjvckxpDxfmpxAGmgWffTFIXd02M9oRzm6p8IqJs3KIkviDVeuwCpxH6WjLciR3qzm3PMlbbadfq+veb1Lzzeff2tf28I1N1au37QILO4B6op5mgqYlGA8Obur0zbslfoQef83rNntPzj3AbUP3jdSrQK8JG5XdWGM8nu625yau9SHRwSxQnedL28+f7vHN1XXevTrmaPnGyMwBohhw5GqoPZD2/HBzzvqI+ez7LNizTrw+tmXpREk/JcNp2npondyQ+yxvmolMXt6x6wfZ19vG8Gx442zkQUHKYEbyKE7pR2JLkxKnbuGme2L7DR2GHpJwoama+81ZstVPDoLX9N4SVbNkeHDAhWFqEakZj9wwaYSJ55xPWcNjIXifPHnpeMtFZtb40mHci5k+tP4dyetvC0wB5xu5zxywIZl6bT1WEzNkyK148v6HZbNm1ZrZ6g9bAzoxPKlCxXdb0dUmy3GFaoXOCkzJoEz25idsAkbP0/9QYpltVKZ+gIl+nchFPoaJPJIVWsnEUihxyxOKqKi5BQRFWrcM0geLwV7KDLE+cxgBH2sE3kIlhhy1MSLY3kh7L9MVqOA6grfwGDdbppAkLps+ELXlOVflVQjJVgYyWtPMRq6//3rKSH3rnfm3nIY5cd1O0rtlA0NqD5zwYPJNRWlgIkbWV5es1hrLcO0RXZZlgtDX2xpJqBJXyKzlQ/s1go+hCmoKo8GeZQN/lyPop/VpSCrK/vskA+/mObfgyIpn1NSzpQfP1aOQRVerGKCwpr0ZSdGiUxsrXZupFAlbP329o9Pq4TR+HHbKsfb+dzHrBqI06fWbo7hI6qKCiLM7rTLugWg+LNWUPf90lP2HnA6lY52clx59kDoyIDHBRQHAq0q+d37N+695hFpvHywMY2uDNkVc31pT+KIeUVJQVsb/TitNzDR96eVLs8eShy+zr3rhH8dr/2KvZPOO0vJYe9Qiqymdi1KmExtsPguz7B2MqjLdO7UdukztMq3TnHicST1HFN3YCsVRqnW24HIXazcZ1MP85uIW34vfsKaDN2uJl2S26JW72i/gFlwp0xmxd3qsLIkDiKNqqnQ8GRVLWam5JIMu9XXQ0yxjt2cErx/egNhpCQLxyY02sXO8pW6dliKV7L4N+jv0NWtmX5v688RZwD7bT6fSZFRBD0tAkacjwba5ekGqD54Wb+gRsi3E9sMSl1XeZIfE0NXwr99QiKLp8/ploSNQ88x4S3Zqurg7nYcTz4jyWEJCviwVFUO7151IfqTRurt8w392zDti+XGxDa0OZgFiK1h/zEl7hvUUHPul6HJjZ+FygLHeYNgB/jxPmbwXivPL1cQtEKrqvjY0ybfnemif7lwf9MA6PDgswafsHHSDWqy0m7rtRisNORi0Y2qLylflxn3PUD+vZ+y5NMFH+j73PivF6VtDWOwyIVSYAG6znO55llNKQkWNauwmk6NvO07dt1q/q9Vbbba8qIU6+AFH37Q8kddLqSN3ef5PeEK05Z93aV/NDvLYYfdrirNtVYyOIVyEji17dvPJNc1JPKlD6ctfJt6D5XEel1osbozn21Novg0JCffoeS3RW60iKuJk7N+x81Dvwr2m95driDtMmYMEJ8/dBMva7s2eS5GtfCBRNr9XbCbYLjmeA7VJKEqxn70yeKJDGoGDSmuUg0XRhypn2RfCvAd9r0ZJ106WqQ6zibzOivzHLxF6TD6wdLdFdI9CqetLVG0rRrG+3fcamDaCU7fbv3GBT0k+zCwdGUGnKitXPNuycPufWdHFJQ0TLUbNuBYzv1aZlHkpj2OKk9cZ5/TpqQ45WcXBbZGc9ui+2be4wbQIWnDB/H0iSrnUrq8zGtHuERyroGg/tzgj+NaDIxiZmzXn8bVlGkfUGN5uivxWCzog5Ol0cJkbNPubg8EhGeT4TRVNRkGufMgNnOGKcYYfjBkn9RzWnGJDlDtMmYMEJAwMD0+2AWJKyHmy8+h8BFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7QAWnDAwMDAwMO0AFpwwMDAwMDDtABacMDAwMDAw7aDTglNQU5ZdzMQoqWuS4G9Sw3QEISMr6a+3Hzl6M1wsVOGZHMx/FYjx5ta1ZEhr6BCbAQr/nIYOVaVd3PLdbO24XqT/xgguKLt56jJ9pI+nBqbb4uhc9dFfbdBd9qBK+hunPWz9ooVLLagoQFj4NHLKBfTq0MDRlJaqQlj+JHDDBey0jbusWryvXQjLrkZuiMR4nw+wUv5vtIP/NBD95fy5y4+JTN3saQ0/bc94v91kyT31oGOPJ6g3aaSC8rc7og8d+fCTjlEbG7Dt4FBqZz6dSX+7ffhezoaokHFk6XXNez+fxWeUgj/tmaDXqd5R82j7DMf7SpFHY/zVOxNOB2L+X2QBAoCu6V7tCaiFVtE+uqyIZEbQXNFBzLKsO/ePLT008FRcqJdKWyNu2kQBztekEzu/qvj5jBvYZlknq5i5P2/OWHEg3WnXSuklK/XQqB15Ads3eP57P0jLK3/77GzoXbbSvkCHtn+3t310rtGIICEEqK08cDgI+X7fnvBVS1cjYves0ENyGeU/S9F0vujPRziFz/ddybD28bYhACIeo6ikFMNq7r6Op4lfWVH6E83kdWWgMN0EVPwi/iRj6IVToeMbz51ADFYo5Ijw2KYtVFB8auvqNbm2kUtm6/Ho2N7ynewZQlZxahaLLqy/RmAIkJAlwhM6O54icDiIzxER//ffO+zuLNCf+wZG1vjHnrPu5Mc+6De3BARx/d9usKG07QGZraK9dFkRyYygmaIDyXYz1tq5O832XhqRXDx5kkYbI2/aRDlZcYfjY4sJFf3tL7WlClqoL37eoS2RD/T9X80yU5D2P4hb+jW7oELQtpT9MyH0XrVx9We/jVN2m6WFDFPtFtHZBe0GAaKw6j2HbQpDZXuv2nri3ZwN1rpOm384NXuzsPhF3NLz+HNTvSWRq425cq6rvwmHUvMJP+fTxYHCdBP8kp/lkIqtEbHpbBiFJxMAjIJcU2ULRP945C1v8PJ5AUOUukWhgMRTsQCOJNdpeYckymMBDEm++9RFMmPu3ixAgsq0vEq1zk9MIX5xdl4xFWh7SLJaRbvpsiKSGYHM2ifo2KgAt3LLOYAGsZkH2wCu5+KViykZSh7mbZq4yK4vYcHjmJAvmssPj+3zD/+cNcR4lRC94j570rK1/rq/y5SVk7TxSOKdjCo5XauAOTO9dPC17ija8F1BSX3C9oZNsIw262Axt0jXTbhAiqnPQNLpt09SaqyMUvZ4nAeWhiwcRRZn+cvhY6dPv88VGLhvMksNOZsJiMB1K/xjjWadnS5YH3oO4bF+z0AyxEw/HLP/4KdqqqnrLn9nEwIoLH04P+K5xSSzb5eu3C4mjPBcEuGoTRDPkZ6eWHb+r/flkLrRmPAAdxsyUlB8f96OF/29BhdcvpJtv9jjQ2QkwuPMAisqADAzr684mPCokjLcPXD7aF2CODmZt1ftv3i3CGEwdM7R2Va0f61C4j+BSCAQAkgUCtHUA4WXJ4JYRXxTD6imolKIN6Hi/pCa/IqCn2VYNYM/vHjVBel0bA8NKqGJB8QpLiovYQoaDSniIRUPEkj45qQyr4ohkidh2yawkUQyAYmVJ/6RA2518fcCJp6m1UMBV9f6BGw6RyRHJCBqStNLIA0tGul3s4Q49OL0wmqUokZPFaK0vwq5NWwBBgeV/SzGaxiQEVWFeRVELT1SfWduKQvt4o8sCDh0Nl/I4gpFIj6HVcUQOyHQeKIcqi5n5cU/s6qRNA1NLWLDkeXPLAtqmGweVMOGRCIhp5rBEMeAEEtFfP1TEK+0IK8Mr96b2igXslqFBB6jUiSn0NbK+aOIxFXAFqIJREJ9yUO8mmouQCQRAA6TCWHkCbU2HAIWkyPCEYkIHoMtxONE+T8riBqaVAQjK49B0VKv37uUVfvigRKJQQICAdSm6ULTJipOFKtGCOB72gf0QhFxzTwhYBR9LxcqqqiqinPScn3xsg8fe4oYunlejz/FpkjALPpSyFfV0VBuZLvyRy+TRAHh5Ai1BS9gM1kiHJmAEogLTapJROHkiGhhZWFunkjZUL1+IgHxKorzfjCx2lpqKrhWhmAhPSVqe+jKpyV8gGbJhn6512SecQ44kGnhvXIK9l3C0alzf7CObPVTR0s9kRpD5yzR9g0/krxit7NW1w/yXampwOkZqgD3Mn+wIYOytHtvEF4CCKj5umFx4KaSfvNcR9CI2rr6cmP7vv6rCD3UzmGgJg3H//Dy7RvESD4kKDy2IXBedv917gZP4yPsqkmp6+2UBRWvX94+nvrFZexwu6oz+7fv7G+6y5eGAEQIgyGTXJBfImOiJyD0vq3qT+SXvXp17/rX+1yqVTBFVPjlbRLgwIMAYfn96Ysivw2eE6T/ZPmW1USdI1t1Mtat3npKbdI6V7lSlCIRlpp/NxJlPwL8c3hB0sYmJzqC+F+zRSGroqyMJxJUMLkAwK4uyyliisdasqISBS0seR8/fWPcnQrJfYqm006GzByjJGnZwsr3W8I3rntdLvEgma5esz7UWurBK7x6dKv/2fcFdd2wb8OI/fZcnwbiyU0SJCiO3zDb+wlvWODBO5N02zBBR2q77Cl3AIkN57v8gvidq+bcykKQSQI6Q2lM1NcVklVD1ZvNPUIY4cHq+3ddTxWK8zAkZnfIPF2csOJZ8PJN+9NZaAzI50HK5jOvhk23Rv/YOGfpayvjb1ee5Co4n/KmL4l6WqTo8vD4cjtii1loN02zQP8Yobc4qaL2InSyguQfwX3bhYuDCMXPo8ZsSnjHQuJAIQcij/Ddcnm6MRmUkWXmx7kei+IZtQFt0HWR/JMfuj1n0yAKICz5ED8t9NgjHhHPooPGU0+HznKi1oujpq2iDkHx3cl+YVd4prsP7Fyo24b16B9FxCu4Otx7Pxh4+sUkTWlk1Tc2TRmX6fb+6NSKXR6OP2ZmHHTTFQ8X1c/cJqxjrU6+p31swLKvTsa5+56UqIxZt6Z6X9DTClWXqNRl5uTmiq4BCCSIgITCPz0a0XwTrb603NUrRepEGHbz/Can32tOqOrbtaDNMfHZbOmlsk/EsUhkpIz6kjzGzUs+nUu09zdtaguCQDBe7DDee/ObOI3y1vuiN/nriIu0+V7G+LRTf8mP0NOHAtQkpZO41nUiZ03JPqv3OzwdkujiOwct2zPtxcbAJ2UA0CvqzIFgdRSv4O681duPZiGUScJSBnlW5KlYc4LMcuB8WRsUHCPvdXZt/uyw1N/uUMX1Q0eTFbxeh8zujwOEAynfvSK2XMucOs+wLiys1kQHnQ3Hbj+sdJre9cqprhScKKK8eApUU8r61SaEuQ9jtn5XXX1wS7hh7SJa6NHvzMqHeAenCZPFi9GyD7X3cXPvRLwGxm1cumEYKRvz3iD6XGKp7SwURpw62uiVJ+YZIdJYN+ffupfH9qURtWxnhkkeGqKUcs/p3YvvnP6WKAwaEJapzf8U7dkXVRZXFzs/PelkItLxXtDkYaBp9oM5Z+7/WO2a+rCI6LTUd/GA7li/w7QTQdWn71UEVRr5zxkMiCYS0b8vobIzaz38Uuua1veN069I/muuOnRkA+mOx4qj+Y4b0/2tST8uei096LHL4HvYCFVhQWzo8g2loy6c8nchZEZtXLoydKfpqfDJVM6TAwtdr5FXbD4fYqVMv79YJ4zbMGIMgdjM0CtiFxRJBoKckprWxrxfOSCQ0Y1cyp/vmXeLNXNXYpQlGcGtKubJ/R73BBnhR4Rzd14KkH86LXD38kMv3MLsVIi6TpPXB9kMMCSKil/H2C49GnzH8blYzIhYb17IHTm2+WTAxjU3xp4+sS5szuHEPI5dH1xLWWg/TbJANluRd3spVHl3uFc0LfTMuYFykoUiRhIpRXfQohD3sQN0yKKKpJhAx2NRJxwPB6nLyDLRLPbinQNQZfxCz8UKoekbrMgSeYIRD3mCojveK0/SPfcWexvLV79bFbTEe2/ftBBbFbAuQY1aRT0QuyxbUjnFeQ1WJC3nrEkRYTSGzTM+OPf6w2/jvY3EHtWfj79l9Zo0og8W+EtGECLW1xuEVSnhdwZvOhw3NiRt7YkBsX9945gPxDVTdI2i0pavSvucxbXsJ3P+VSOjiVI8ox95AsK8a3N1Yxo9wMu/5ha4673xzFubJ4+kCbNTUyt1CGSSzPoSl1n599eZqF4bDZvqexHC7OizCkv23/BXfOnpuzH80rcZi03QBdeb7WVyzaefOHJtomhJSqD3ogdPIncIJ9yOd+4LcOVp4hGdfmPvjqNM53vXgu3JCE5VBVtOKukYb+at2PeC07Cc9JZuWDVNtces4N1zTcwUUjY2ioH19exHjp7bcGNpbpDKA7z0AP83aSVCQ926wQTTY6CNbtzNB7mc6UqyBXMH6UrBCfG4fABAE38v7VlvH3/ha3pO7oFv+cnq7PcZgPq8niQQQNF6G6tDSY/z2bN0EOKFCK2HivhhiKKqALALmXW9glfxJfHpm7sFPKCmrFIgmSKJ7zR2GNoLI7Ueq4895XWugGiV//6vRIAlQImKskoFir0HUZlHY+I8dPzHqTTfrmH+J/C+J26bduLpd+LwXYvMW7cNAWmz9z+cLX4s74zltHizXedOWtZOfXifj194iBqSMHuoAQEEjCfucEu0OH/zafWIsRV3I9+jxofPdtMUe5gs8Hc/7HfuSEr1ZPNP228U9pgYGmKtKu5PHCwKAXBbiV0MWndJ5MlB3wVG/fQ72gshLquaDXBLK1h8gIzDUtQajJuQsJo0duEKc2Us4LDYJvb2i+SPNXYORHUXxzqjTJrJSFfVC6dyyrkATtzV0GZO9sroB1jOh/6O1lSmJo5XWtNGmdEJxLIND0A1aFA8/qKxcvjf/RqrZjNNrfan4uCRtroX734Rr/PVZWUZicXhsRALg5DISzweXz/+CnKeXH6AtL3ubiyxVaGYBk4y2Bl94wXLdlyL23kY3SkPT/R9J+hhq9+c+rJNWaONdbVYGHbzTM7ksJ7YytTb91k6S+20sIBMOxkhD2XnZKmJfovnpDs4GKmxlOV4VYzWK4FgNc3fJyTSasrD0VPWnvI0aKY50d+0s4lyU66feQhaxa/2Hi21hjUwHVSbK1n1JRG1WeWQwhCdPwpMBPAUxwUEGJIwgOUkPfBadikH4GUlNd/LRrWcVxHvy2f1CyenjlKsFwoQn07nAryqIpYAIGNxFKW6+LEaruMnDmxY2EiyucT0AWfQ30xSJI0DFjAKstgATaf+caScBhUDZBeX8YF6wQkQVPQ1AHqGuMcA/2jByS8vZgIoDdqvXQIhq6CcB8hrqrai2BIyq5gCAK8iNXFDyVGIALukXkaCtWq8Om2eSFxiuQ8iRoYlcXqa9+E3CoXwe4ekNlR2CUMA5N/dEPNUUmkILRNlLILQb8f2BcXLosbPLdm3Y808/abbXjD/K0B5jT5DjXMzkj/8lVczQ6e1jQ6ZcDI+FwIqzn3qzIuwOoaaWH5xBp3Pyv+cBajM0qnzwKkaGqD5efn0KlpKCodoY6lZ25lEkLCNxilIos5Qiw6mUgqoOnjO6n5rwsI8bhzr7z1h6qqxltq/u4aKk5WG9ApD0yAD7Ioq6cIWYhck3795+k1mTlnhxyIACYmkqUVr9VYjABVIBFarJw0H1CARAB/ofsHZEhCr8MOZG/fu/SjKL8zIlqQUaC3Lf8LJ+looYH4f7Xy/gaMRnS/zgXqQZB2z4Z1KP0gb6Ookt+bE7YxVPbWf33lTrTfVXVM8E28sOEXQ7y1xtIqleCJQgQSxKmY0LJAlHqMEbagEqKb424s8hLFN/yG6pGYH4JqCdjZRiJHyoRDQnT68HSezIA6LB2AIfxoLiJuig4WqdDmOxGFAEUfUQi9rLDhFwj9SSjR1GqHYIA5Qcdxcb9s1J6Z5Pt/Yf1TA1GlzLGgS4YdSHNDfitvwaQSKLHubHhLwxBUjEv16AIElYMQl1Sh6FI6IBip4gi47OtUg6K4LSlj9/lMxoOHc59e0BoGWyFAeQzy3aDEiBFZiXi6okWZQxOfxJcvW5vb/JZrtx/7b7+C8D7zz7ZEZ63P3SqNwGoeKFg/GqH6Bf0XaKzd0N3A/H6Pov2R9wLoTA4/M69/RGSpM50CpWkzcYeFgu9bT8+LHrUOGK7f+SPNA4s4iatBjJJ0JiRFLEqkH1NgDhUICXCZHPCIga7uSoLyoig/8jxoBKG+2Keqi7+sbkZevHtu76ECC+/39C0bI13qSdCl1NjY8rgDAkORAQFCaPC9403Ulx0CHkc6KNZfyI+rkCQIkyOMlY6TEUuafsFEvyE/eOSzsmYaD21R7a9WaRxk73tV6tJjlZhBXGaDjlxrn3fd/rg8Cyeb+tuSRD2688Rh26g3bdPpQvT/SIGCWlAlFtatfBIhTrKsE+fZYS7CeXbrxw3jZj3X2NBnDOdTeJiriMcVzC4RA0A5TZxArhxZx6Kw/Nx4QJG1y0/FaZi9riICZRxdCjVd3ND3Vxg6gounsRxfG3L1xPvrarQWLru533/0s0FKR8XS8W2hjrbjOlhNHVuo03w5QcgriWqCXM3gAVSrj+ZWVbEBeTbnh9g6/plqAJMl1x5t5uk5wcrJv70kRmsy2Fbe28lonUK5Xbypw5/Xbaje9ukkHAoVGiOclgkbzMvHiQ48GvHhTwJmlRGAVZojnNrPUmm8o7MLPn9iK4wfoEMWNhdfiaSOQ0MtAUfD8w5cae+XGVYdRHb5tzo34kLcfGAAsOP9WsBqaJOGbSnHv7eh5a7S6jgKQlvqVBRlKToKy0z/n8sjmZoooLF1HBUh7kcuCdCQerJ8p3wRku56KOJKSPMDMkmg2CaCg5P7jbAAwbENEwvK0uzEvuYPHOg9X6sSgDuL1rCbusXJdemtp7623D3xZMMKqzgOFkA5D/JLH74pBHY8+eO7nszFH+S5Pti20IQCCwoQIibqqduhC1I9Yzc8vm6cmMy7u5GOi42Zvm7YeIWw2B+JODPAZvAZ9mJu1/8BNrkv0jQUmRECQdfVM2a+UtpBlEESjAF5Nw4CwmnpU4Omnj9VQX2p7hjsh/WVSwi2uyZwxFuodrxzioLH2GreTj9znPmQbrBqiVrsJCiLFs3kOR5xKpLDgw5MvADCw9nZEXS2I/7WnGgRVFVyijmIjZZeQU8UG5et3uVDtbaJIkq4qHnjz8mXVWO0/yq2Z+pKA0dBRRFRmfmNBg5vo3RD1TfE3MnsZUIpEivgsnrR0yj9czQGAPo1Shic2s6YF8eqjJy4c7ep5bNlU39tXX/lajibbP022bymPTUKQ07FWAaJffyvz1FUXR1CddildqDfOqOGpTXbh11wRdQqtO47adIHgFFQV/0jOfha25/hHrUn3xzXUxODNnRx7Xj2zMPKK8syBigKMgQGNoEAlAKmJLzNHDBWPa3UQezmOU7xx5vR9f3WD2+fe8nvOdBU3/+pmIsMqaKggyp++ziikVh9LLgZEfUQyJ1kEcyd73euXF52wvjDVGPiZw9bsa4QufPBFYNxD9OBFNpdsqdfK3itMt9O0h7YbvMmIYTqXLq6IfWgwewD+y5mghNK+U9wHEQCCnr077VLUgcPnNfwcsWkRUQk/dTyC+hJwgPVY2vGo81cem4/DPNwdXqjUJjUxN3Pnpi1bCgDlYu3MlRYdO/lfk5N8pVjHyVyXIixPz6/iAUpGSr88eZXVbB6F9fTCzg3f5T3C7LRRQAoCATHz3uczTEhpO7bFZyGb6qLaBevHtfUXH+QDb5Fm5460YMfYKjgVQ7Lw8v0XmQNtRD++lqqaWZPE9Siqyk3PYOgrfDkzO74QJZ4dt55lnJY2mf/43s38gS6izDdVasOMlfRtxw6Ki160+4ruorFWFEFh+psbuRpejvot2/JxMs9N3RKfCZBztc4dseh41uR6OvtoXA6PTUL3Wjy27s0+YplBhe4kJ+a6qiEeLDtdqIru7BJfWoW/270g/8Igr71A0NkXE9XrthU0ZDVRAYvJ5otEDK54xSesqWFUiSUTgYBFyg0eZ0d7cmv+lpOEAJfBitz0lM9FPezG1r5z7s/6ksz8QGqv/nrQuXOfqnzsFVubpMjsZSglXTXRnUvPcv2piHMxp7IU0bXzFslxFBaHC4mEvBo6g4HHytXPCjhfkx/n6AwarksUlP/MEK+llXqot2TJJijP+vaVCbFzxI2HV5iV9peQoKrbU5+o7+2ks+v44RV39SKsUI9i910RWOwf23CLm5v+4kU+0dhBszvWRp0TnAgEEgRK9q+Ze5ikPshuxft5TqYSJfjvqQ2hj2/i6upJu6OGJwPY3n6v93obmUzy1Xq2b4vvs4wDqR6/7uu3dcPM9NUR/dwBUH3koS3ufTHNbxagVEduc090OhagflLL00kfdZdVI3skIRrPvrG8auLelfpnxFeagXtiI0jJa5cffM4Td5E+C9f6DYNNa//9yPWdeWlBhWd0qEmiuEUq2nluvjSjt2TsxPcN3bSgaGO0p6/EQ9XMK2HTDEtJJ+q9bNGkhyEnh086idJ0iJpjFhrxs/Vo0Kqj7C0u3uONHqLd0YGZm/X8cnDM+7rjAXI9fZZtWKb/yzdn3Zwx68QLASWTeev3b7FVFA+VfZ19PO+GB852DgSUHGYEr+KEbhR2XHLK9Rwf1Pvaym/0L8XsTplLEPou8Rl8MzLc4LH4Qmni+kNnR+jOmmEfvznS3CUSUOofEjSNtfGYQNhqlgmDpviOe7F7upckII1h61/1sVfXnnBuU5VPRJSNW5TkFpBqPXaB0wh9YosjFUZ1oKfFo9O8ga46nVteYHWnOuuFH8qxcrbWqosRre/gN+/G6uUzRy9HqnsEzhx6LCK7U3E0pfrH61SgV4RNg1fw4WQ00eq/XF3X3atTrqZPnOwsHtZCjhwN1ccq9F+QtBzpuz/OxUd6qgCnM2OVxRgNJYnAbaa+JO44bTtPzZM7Ep/lDXPRaU0QyOxl6g5h4667HvAlHUDqjwjcYHpsbpHYlfkoYrLDPabkyTg/lTjANPDsm0nStyRyC69fiVr2Pqw2WHJPp8PrPWVbF0uCuhMxf2r9OZTT2xaeBsgzdp87ZkEw89p8qiJkzpZZ8eJKotls2bVmdsP3MLIz45MKVGyXdfb1Vs3TOcFJttpQfn8FS4Am4RoGBKo7HxI51/7G9R614pPDoiqGgEiWGv9gLaNPJIVWsnEUihyy76tkl9r7FE19Hl6bUlzBo1DJtWdpQSWXX76gmvv7ZPfa3/ZBR6q9yxl4qjIWPL1M6iTv+ibZtT5ypVkHH8+qu8D3dV6X5rSiopKFlCeT0eJwpz677VZaxZdXkG/jUWmY7gSJx6MBHktyiKBt83iMlmdKsmcjJ5Bo6bbh+/gVRaUsOWWlBq8OAMm93c+eco0rL63GK6v9slkDkKrWQe9uzSoo51KUFQgg4N/8W64aA8oPmx35fXbbstU8WCOPqFI3RmFJeTWSokOjNNaQGew+GuGlIq/S4LgFRm3U6TNDd5fQQQUVZRwIzLQLkrqHn74r/U/efS5R+sP8yOWENsSv4TiAtvIbNFhHxiGCtoLpM2FLnlNVfpWQTFWQdiugx6j1mUOD8uigiookX6F27m3IslhOTbh60am0rEooRxVnXOqJ1h4858HgmYzSwkKIrK0s35z1SlMkO6m7T2/qXK6kIDA4LBo/IMD699YBkmoTc/xOaFGZgKKqLm5FbrUvO5uTfkf6nxz045r0h/mq/CvNhNgUIZfBB7AEdH222F/fZID9fMfSGg6hsprosKQHj5sPFiSYOC9/47ykprKsDCCpkgkNdvaaqS8JWD1/v6HR6+M2fRx2yLLupbckizVlD389KD9h54M6MS2rlyGpLktOMGcW5Qspukri0nH3lTqPXHdTtK65dGJ7LI1MDGKU55WzUBRVbUqr1Uvx2v/Yq1kfnJbX0qMeQVX5TIw6ldB4/BBk3z8YU2G8dWq/Tp9mbpZOq2pBFL55y7BGN2Eo5AarcRBLpTY3x0DiacptUZ6COIpyO5bfIEaR2iB2JF6ZCqto/yGgVfV1CMeTE7Lde/fsnIUzEq+q2my1IuWoqs0IChRBndblRuqtA2JIGpokjWZ8EGg8ReVPIxNxp1DrkubKzX4Rv+DS/7F3HlBNNFsA3mx6SEhIgNBBQVGKqKAUFbGAIqICdlGxISrYe0EU7NIsgAVFxfbbReyoWLGLvaE06T0kpG5eAqgoCRABRd98niPZ2dmdmTt37526m6U/YP3Ctk0weIUm0PQ0fgwh0g1k5VR+katvpMbUqBWKoajpNktXoU4QVnLw4Tf0XmHOP80Uwnh1LbklUAhOxp0jaRjjYcxqUfEy4x9DHjMd9Gs3HH9FRdEkFaaezBO16ksSptnNZ42F14wNkUOi5g2kN6DpKvspgwkqWoYyYssDxlPUjCi/vBzwp3vRdGs5E3721TlRzw1GRk3UbaY1Zi3n4zaA/0voVlPW2M6dMdkl1GLqjc0jTX7/m13/PyhP3u4S/sl28vYTbuZ/73cvmhFByYsnN3fvj4zk9z42yaJZuimi3APLfCbdK1TpOu3itzctoxnDloYZGP/+RkIlWB3vFcsfTPMfvc70+ToXg3/DHfBSggOCbxj73vE0buTQinz+DUkB/l7wBtODjo0rzPxQQqh3ogXwy5AtZr84DIPZCbmwHs1aHvrOeNCBLVPdVZunZYFWcZq64fkC3TaMGluIMPSOJvRmSa5hYNQcIoID7PI66PwzTx9W3dF9joNtf5NmfHP9PyMswF8MmszQ78T407n4c9BsAksTmzsR4DXrhGZ/6owDtdk+M1YJjtmqLbM5E/g1SPq9vfX/dCaaEJhi1a+pP7r1M8BxAgAAAIyj/oEpb8BfCnCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoAHCcAAAAAAAoQGMcp4jzJbeYW+O7uiisso46pcHft+A8v3giHrLz61/P590B/zpIyevj6953XD6oLQW8ULWFIyw4f/BkaV+vUdp/xYdsWrpqCQvurTvJHu3V1/CvECegmkY4TqQoYcioTY9qBulOfLnHy7SBGoBwHp7atRRieDkZklukTgN+D7zM8+MXRX1wDlncHHfnPJ3iNfew6sznW9xa/9bxFc6NjeOdElTD9kZO1/qd6cpHYVHIKgK/8PHdI6suV6hu93WkNewrIggENeYB575bvWjVnmyB5Cdea9B/G8ZaNPirF7JU64/VC+vpRvN5V7X8Ym66aX0TP7fwXdzRmFgu9faMLi3pc2/lCZtmzeZOuLGi+/ePL/y5emx5NMKUwCq9jh8w5/BSNy70P2WyNGFKOzKe3gq0mwAKIcjYuS7smuH0B5M6qjRH+wmFIyEitpjYvN+9kJUwgYAIuGJyy7EOtURR+iDQbHXeil1h3pqVNpt139NrddaUmKv91SqrQlYRSMZLVi99OWX1iNCOr/17atRj60vPr5vhx5v+OMCO9svZxmqPnDKvG4//MW6dz4tCDtLgC2Wr1h+rFxiHF4m4YiK+piaSjT2PL/lsFbhyhsWBwz0ZLcZ1ImU5n19x2MLqwz9ajy2RxlgTDFlfjwxVcCTtToySWlsDgz/0MVbA34so62ak/xudhbtc2/9oyBDW64htUUe4vXYtc2vfmNYYmsjAQwSK0m+3k2iyMh7CUZSboCmJFD+LHh/9lK3rsXduH71ffmZriUIs4paw2Dzo23SLqLycVcZHvh7LLgKG2SvE70r7oK1BbpbbOtY5zYIIclMzchmQuK5I9Wab3NbMsi3EpT4goF40/DJ5qtWE9aIYGCKVBOFUlH5KGKPXyzf0iqfn1v0zLOf0bJmzVn+yHlsmTd0MFxXe8g06TRy/KqQjmfv5xIStL+z8lkwj3vIJvtdhsNmrE3H3+PqeU+fM76D8U++iPOXcoh2nbxTTenn4buxvQJJYzpSLSyKOX85BGdl7751szWwxjTFAk8FP3RVzG2W/1qdVTdsmKnx5fPKqqNN5IohpXN7IlqnEWxBhEoX4c28W4RflZnwqx+vpaqoTqnRLyC7niglkMorzJTNPpKarR6qhcwivMDfzcxmaqa2jS658bER8VoWISBB/ySwia+swUKzPGSyarpZK9TOFJlNJaLwyGdW4/Evgp0VtPRj3EYFK7TiNMV3yRCH/AjlFQGvbe8/Tm7BmT+KiUBdd2Q+mkFNewUc4FYhY4p7LWCzJPVAS10HEQEJuaQVCUCLhK/MhrChniwmVH8KsU/5yQXglWe9KCIZ6qko1CyZbteooFMIry32fVU5k6rZSqVYISeZKuWIlMgnFyf+Qh2jrMinfc4RwS3M/ZJdh6Npt1KsVgsepEOIISEFmLlHbiIoqyc4oIuu2plQrBIaoTIbxdGIthUCreXiPDJq4f2Xi6AQXuXZOyC1nIxJBQaU5aZ8FjPbaNPy38tZWzvoyI9H//KyMAqKWMeNnfUC4RamFxSWiKlWTX4+VpxCcEhkH15QV5hfrUZKjkk8ZJUpaepoN19A/RlM7TjE/L+nJQ4qrSPJbWJ5683GySrkIwuTff3Al9vUHt0F27W8eWbSIpx8bOELl+1Wi/IRxc8LedfP2M7y1cN1Ssv6e9fofVyxdf1Bz2IohSvkYOhl4zX8RXkbioXRyn+kWajWeFM6b3fYzT9NHBxzM3DDmdaPTQDOnbDnnCROpNcL4WZd9lm7c+xmlRhHls6iTwg7u7kSCWI/Gj1xRPHlm69Mhu1MlCswYMjf04GBJG06Uey98QODpJ2w0ARZxEWrvCetOjjPDf4rpsuCts1n69lt56gNWLCvb7ne7SGNg+KsFnSrTQusN3FLoCJMb24cQ5dzdvTnb3LdbakRm4+4kSxR1XyC3CHjdoY76ATEXrxc7j1OVZebKk6eOnBPLqjoIMBgo/aNsvzEt0Ab9PNhw3qdVh3bOkI4Pl8UtHzKUuyxvex+GXPnLRVT8bF1QwKqnfBU8Ox82W7xiVaCNapVJk6lacgslyIoNXuJ94TOKShGWslQHhL9d1IkCQSWP1rbyZ62ZqRURcu6VJEf07pGh/j4GBFHR3ZkLAyM+sLE4WMBH1DpNPBM0zhb7abX3/IfWZu9O3UpXcTk4tnRe+O0c+sDr+xY6kKvE75oY5wQTZSgEQdfBU3/vqktPc537a8n2GpybIaNcc73CtU5NP58ukEjHZs7tQLd2ONnKSRXUkRlR3rNYz1UxN/hkIrsUNhtzaNUkZ4ZUbLzsWys3hGx+WiiqStOkrnqkcZKnjZr3YuLhh27Siiy6u1zTv2LfmYiRsML1KKnIxIOBI2Oecsn4slLYbrT/f5NsNFv0jo/fkjkUBoeFIPV+C3dPNUP1FD+c+l/Ew+JhTt/OCz5cORCHdrrqN7wnbJF6zftwwqelQ15dzyE7z58wt0vLHLwANB6k8P3DFEzb1e1+GOMntXIJDxnUvSPldmCTpALjSOQfR8dK47du3lvucvXszD5UFLekqELp20MtTD6wRzgoJNNN+UzQjBmROy/YB3mooGkGNnP8PVy76FPFRVcifZ1iwvc77ZoiaSay38aTlrxYc6lb4K5oV//Xy/d32X3nHbdTV0JlwlgSFdvo7Fe8D9uVpOYWMrDIv7GOU4Yo6rtAbhFwrbraGUSfv5bOHacqyySSO+4+fikKKY6dPWquyqoPAdYSb41C4yRRWXUlKFP+cvofwpwDQYvWlo+6eWacLans+k5fpzXbbPb7D5bGl61a8gpVeG+LzwX2xJC4cEsqileSy1f6fpnw45o9oqnBJ2Yo3/b0DV24M8k9yEGdbOA8fKWfXZd2ZHHuw8ge8/fOvOR0b6BUIR4lKe2JWXtgxupl8a6H9q8I8t4Vl8F1aF+tEGSyHIXAafaz1Vh+4ck7bn8tuR4Gxf90ZC1+2N1zQ5j3V3UI3L/lnVuEuWzl9GPIzUx3lWtjFx8oHbU1d6yZctmTJX7zxm41ee3fQ52bvHD2sh200WePevVXKz88b9hYXl31WCeK1CMkTLsc5HqAvWDL2WVmpMInO+3nB80xPXCoe7OseWgifo9XR6ElItBqq6kk+a1jZUM+nPg6u8JJ8+tp9ouH6UKy9Zend+IgthAjzvmcL6Qb2zDK90ZGj9SfPki98eYH0ALhf/lciKh01yf8GEzQ6dtR8qe8uZJFBKWlPIhfksMWQlQ8gab6PX1EVEgatG10J20cNGa43YoHSSc+cjy6kPGadp7V2krv1reHwfHLbwol+YREfIyDs6UO9jGR+8HR0VSTrabEL2E15aoHYdq1HRFldjEehsTdTXjbJoCkbqgNlX4slBhXmVYUjScQ8Qgbh5LaWSKRqNSQm8qRv8y4wtxbW5+ih6wfaivdaEKzdx/W8ei26Ffswd0pclVLTqo8dlkFxMsvYgsgKgFP06wxuIuIyiiusxd1UsNDjnPtdl9MSkzmODiStQY6VS/JZZr3HaJx7GCaRBAECOFjOzr3UcNew3OfWTnZMsp1CPz8Bi2DIegaqqJKM7PkibMyL8IyJe/pblYULGTZyxy+8zpfGipbORmQnMwI0l6evIbucc7DTOqXaBa+w4yCt8UnsXt0e3ooOkdz1iqvARoSqfFJ6Koh5WavR0lFnj7xBNNj/UwzaUWqWbjPNjoyN/5VaffuKrIvaAn8Jscp/Q+GKxsQGCUmEeKUcYTfzooq8lhC6MvlgMjb0hgoXXM1PIrUYfPGWbkLwgdPzdu+eZmPIakFtz4AvwbCZfMhHInwm6sWpg+aOrbHsv2eo+6ttuo3Y4ynd2fmNwOra21dtaOOQNdWhSpyyqtGrRB29rPD8Vevfsr5kv0xFUJXr5/BqltKrGwRGsard2Tioc8wChJCTeg4y1+s2/PCcMRuFzp8v+nu2jRgCJLuUxFf2LhNCmKR6IdpWznylwE7+22qqPzJggGHawTasgWVfxVSLVijm/fSDsuCgkbGx1iNdRuzxNVS77vvVHe21q48wjG1qVBFUUlljpCKrMSE84cepaQVZCfnSBWishhYXWNNkkQhUHjdNhKl4ki8j6BhCoElkHBQGbducapb9dao7EVIfBgsZldLTo5yys4M5/PbbGH5+/4uCTXua1oq4H56+YlNNuurU/Uo/Fwv9SJGfrig4fUIcbMf5oiKPyyg/ZAjSf21ZJracVa1UhBEltCrVAsRsEUQjoirsT4cS0BDmA6+d8L6qNWMb+TxXyR9+ryVM1bs77rHx6pBjUfAXwSMV8KKuaVs+c9UM6VLt5h849iAy/H/bTt7YdacMxEeoXd9LemV5+gatKrBTJGALzG9KlLTK/ySGNwz6K62o/uYPrYanBsfNz+puhEKJtCJ6MqSKDfDNLzgXXzUPqTvqUH6eIjb5HeXAqPRkIj3rQ2L8MoEKDwB26A1OQJOmRBNUcI1qtkjLM8oFSE1+liy5C8HscSg6K/Zt2epQe0RKcVUC1buGBh+fMLD+LCTZ2K2zok67ZEQMau3ctVJigGtykoifImkcBQlGBLmJ/rMDDyn6uTr2NeFzjnxZVO1zUfBJOVqhahSjAaD8DlsAZpErVOcMIWp+rPFlquc8jIjlvzTn/IqeqzJD2LjJLL4En+MqUpfWJZWKhIrYHKFJXklAvH3ilSgHisrsv3k/c/GGvw9mxmb2nGi8RSJ8CQdShFEE1WwOF/dpYSywnI+REeXZ7wshnSMJN3Or8CktkZ04b1nbzh91H4cpsBp9NrgHR/r//gZCwKO858Dp61PRxWnvGMj3Ro8oFCecm55bDLNyXu5rVpjlBcmavUfOrv/kFExC8ZMuHjmwQTL/lXhGFRl40+Qkfw4HaU/34AI8T5HRJ3nDdwWP8ucDAk/nzlcAEHVC/NRVZElf6EGL57lPI/fvS6Z7DllnEvdJeC8CTv6Rkii7AsP2ifi574qRoovzVqdNWD8zFlG0oeh8aLAUTVVoGdvCviQrvQG3LyPGSKV3swGPWkV2W/TxYwRzO9dMxGXVQ5TqDWNHwxjMRCfw/+hz4VCo8UCtjQMLSp8diYNgtrXuKK2/OVAVGutCd2+/bEUMai9PElx1YKJra2HbrEeMv/CfOP1F6PezOpt/VOO8m4+yYX1R7Yn8l4eidwrGHhrw2w7EiTMPr2pFPquEF8L2aBEv8P7/DYXYfSu0dMVcVgVaCUyvkb2UTAaRv18nVzllJ0ZnE5rBnT7eXIZYsKoKRm0ipoSVJ6dWYFAJFiY//hEKgS1+yYcWfUokQws5lfwRZUVmXj7h4pseD1CeDVzBnTmxcdCxEDzrxlXbPKhWqJWZ1Vox+WE+7bWz0/cL4Ew3K/t2Vdn/jtnNwxz9tA92Diki+RRL/16DamTcx+Dcyfn7Lc9NsYMykyr0DExxWZfeyM0ayW+lpTKo1q2li92wF8LzGhr1Ro5evR5iVcf+vdHRlj66l16CcJ7UyKE+IUvX78QkOimbbSp0kZzxfOze8KvFUCPYYcjSxzqW6IgB+7bxJtp+ja9DMjCwsyPJQJItZWWxNxXjg3xWGXlAlrpi2PT9r5n9FkzVB0DCSUWSFyS/uEjy1DlzeHJsdkYSPzrneSKlJ17jh8pgBLgTimLO9W19RlDs+ndn1VcmRQag67cB0DAYbHVZrAJREHSs+lLP3xoz7Fx/sOt0SkRO0591Oi/r01D7sX7kJT0hWzmWD2yJ0w55mO0DQo/vHvmD6/jIejqUQU3r57/0nWgOOVRiWZPM1W8qoGm+NKJu+nTGaijkQc/07E1ez4y5C/d3lAhEPPZAkQs8bgcVokQhSOSSdr2U0yi52wL3a4x19uEJij8cOVeulFfJ3Np9uWolhw4aYmncvWdOxnQRIUfvpTwIVVT1W8n+cVlFXwa+/ax4ID3yiODHPQw0AsUCinPePqFZU55vXlD7Gc0JJY5xtZweJnx9wtoZl3aVovzS/i0UbOhmSmRQ1vXl3sFlRNr2MPVJnrbnNBTBnNcrWnC7A+P4tO1RzsZGtnY6e87HnIq2WEQ5ljo/lQGrka9yKhHHFbVhCE+kHjn3RAG6nrEhmwGvkYfW4F6xGq7uZr4b9s645RGhKuJmrDw6aN7b7X7ehr+4uP9W2h6x9nWd5ztkZBd3UYetHTuY4a+LhFT1RldvU8+48fmQ6ru89Z462FrjvyTzSbHLywZunWxoXS+Qsd3y+5NlMTlC3fck9gypfazl09pofuCAY2DoOcwSufA5ri7GT0H6n9TxfIH3tMD71YfXJ045ypE7X/tyNJe0ueI2Hmwh1XcjkelaekVdSyjqBNe9rlT4QueBlUdUds471o5qgO+2nG+jp5Ci5Y8F6rdB6+87d1DuqsObTBpfJ/YtWGdBoZBqlb+fp7s1THCX/acxLY+7sY7dr7LT8tlQ1BdjhOnN9536fjqA871tY8T3vbZsNizXbU9awpRkCw2rZmeF7DDYaikzBDZ0GXPusk2DblVRUrslSz1HgtsqwvAefEoFdV22kD1nxOwGTFhUFLouNE3JQfaPVc+aN9HS8sxaNC5IVETKFFow96+ARYxU3O+XyBD/qx7w92Xna+e8opzdI+TGIVhG//7z1pvekBQ3rqNM2e4zZSegjVNXbfY9DavfDGSbNWSDe/zvZMzI58WVR0ptfFaELDA8NvZtBXeA1ZIakPV3GdlxLoedEmOTFy8Rl1e4zvZxRdSdRw/cwl31WpRozwnO+XywSya23zT6vfycD5dToUsp9nV/7ILvMLKidNzOxpY4rUp3M49XHoMM2xdZzn3NtQ1HhUx7OnQA7P0DqDb9J25ttNe7++ruGXVI1ZrzOTBu5dFdXCOwmj1Dp1gsXpz9rcLFKlHivGQVSeK107ZMl1zi/Qcmm7qPct6pOFvf9mXAjQ+a0ST0OM3Q78f44wHb8hxLMyHqBqSgi9eIAkS5UpP6DgG3VwpLsaoqFWNd8Oqk3bcnPTtLi4rXjsvKipmo5WpVKwkwpi7F93zSwTKKsr4v6b/DlAQfOvpU+y3rYwOTO650/LrW7hpjncSHeVdQdDu4sTc8Qgxb9eg5X0yE201PyzOj1WYUcjG0DT0aD9Mv3T0jbnQV52uUnPbBrZVv5Up9n4ZpbC6Oo0EQ6scPCrDvT9cqvxL9ft0tvJHpyVfTtWfvFGXLvo734nM9ZR/tQRVNIEoIJhmMvLMf8O5xXmFGIY2pYHL14WpCTsii8zWj+lQvSW0Iu3qR1QPr261XRTewO3Mcef8ghKREkOdjK0UNWPgvP3lE3O+iGgGqiQ05DGhRnwZ8qf0iL9yU2Y+cMxua8POrObkfypEVNXV6DUthUzVkg3edGR4vjsrO6+wDE3TZ9J+HNw1Ct27abS6snqNnSQ4zX6HDtuH5pXCKupSazbRwa8yfM2hy5V/qaFH4yp/dNpz8nRdKVchzD6883SOmc/iDtX9A3b6o2SUxUo7Zg1xknovPfd9QaWy/aWExMpf8pSzTR2Z0evmfa3bRFZ+djZC1VNT/voAMAb4RpdNLMjikXWkc5JuXjVlJKMe0Rp2815dnJhaIFLTUKWgId8BlVEr9xspVI8QlunqHZ4zkfMlu1BEVdf5C0x+8/h0NImhISMYhSHT1WSEfwXG0Rk17BWaqMYAQ7T/NmjNbj5rLLxmbIgcEjVvIL2+9RS87AuxW7ZkMSetG23ZqDlvGE9RM6LIUEYUhqimImOhD5pIr2OapuFws5PWbj3xielydpSxIr1EXLuBs/Z0b6X5LWdNJgoJMEFFQ7vBsfnZV+dEPTcYGTVRt9qXcDPvXYV6hjvIeXMtmqDG/MkeSFLUMpQVV5786wBDUmsrQ5SKqRaMo2jrUGQJAYUl0tRr5whNZGo2iXUSpF7duui5xoLIAW2rxcn7cO8R1HPm0PpeBFwjL7+gnBiKmm7tAQ8MSVVPnl7KqEfJg6TSWqbUFK9HSdraui15eLYmLbgzDPi/AKvjvWL5g2n+o9eZPl/nYlCXQnJuRSz0+2S2ZlvQDPMGfpijhcFJnrco7IXplFuBbt0UKwFGs0Nfrxo3+mOi4KUEBwTfMPa942n8raOLYfTaF6ph1dLeVa2Aav0xuClHRoQ8s/SNWGr8zfWhNR2WJWgYt+BdjIDf8+YgpfY+EyaiDcG6WIAMMGoOEcEBdnkddOrRRlKPWfs+wi1+FKcOSBZbY440RQn+nCiw6o7ucxxs+5vUeEsAht7Gmv4H8lIvDVatPwZOvYvv7E4u/Q1qGEcMs40J889lCdAAfos+wWTjyV7GvyMlwN8JSb+3t34D4jWrq6DYHL8gZw6m6WiyEvypBgRMseo3oFnu3Dzyb6hqyYJmE1ia2KS5qQVMaTe2ecT5x/gtz9GfpqU2xAAAAAAAaJEAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAIAxwkAAAAAgAI0znEi3KL0woqv3xtHEVSY2qSv3zjipOw7eRey9Rhv+Ld8Yg3w74Kw7p+IfWIxfmpb0t/8dZVfR1hwb91J9mivvoa4+iP/NhDW6y0H3/ccN6jTb6gWwZddActO2Kw756oJ+gvNjzDrXuw2tuPKvtr4+iP/dTROg8qehVosSiz7emi14L/TtIOjjmGXrvJ1Er7ZvmsXiu481vD/1FQBWgz8jxfWukRleoV4fg/jPJ3iNfew6sznW9xatxw7ikCQQk+LzPiyisYtfBd3NCaWS709o4taC/mWKT9z77qFizKdr4xpQOS660vE50E4fN3lwqq0Z5RcOXHtQ/8x7bE1T1Qk7ZznneF+IaCvdvNIhpW8tW9o3uxNAaNki5779sr+4LfqU7wGdaU0oPqbTHU5NzaOd0pQDdsbOV2rnqh1F4H1dKP5vKtafjE33bS+5oif/f5ucMxlNjUipMvf+fXcumgCk6HuuzF0vj5W2uOkqlTcKMzMx5YKxBCq8XcGAJoAfkacV9iTDtN2BFnUMEsoHAkRscVEUkvxmqXn183w401/HGBHa2R8WUUjG3seX/LZKnDlDIsDh3syWoAhE7yPW+v3xHBT1GT7hngL2fUlyHp4aGbEsZOfysSSMmrZ+geuWmAk77u/JKsB/fTOxB1KHRrYpmYvSMwpSH+dXSb49bLUg6gi7+3nrCKhnNPcz9G7Ynfnkoqs+pywbcDXwJtMdVEEAiLgiskN6BLWXQQYhxeJuGIivkaOSJZjAmM+Tx4dENJz/0r3lqBxTUkTWA2MMl1dX+Or7J3XfnKW/kUKGn9nAKDRiApORkXf1xn1xNXgB4OKJjLwEIGi1FLGkRBBbmpGLgMSNz6+7KJh9Hr5hl7x9Ny6f4blnJ7kxue4UYgKbi7a88Zo1G5vg4bVgIxCISXJO3rP/6+oi+cubzsLctnTp2lGqnWNRBNa95ukdzjqwsfFbUyVGpf/poTQZu7iubSPqiM7NcBrQk2oumiyMh7CUZQbPXqPIVJJEE5F6ccbYZjDZ/gdHBs0e797nzkdqY1NpEXRxM1tpPD+lpH/QfP9Zzv+EM55ER+16PTTPFpnvxnTxkssGMJ5cWnH/OMPU1HablOWrLGm/2MNEkBDEZR9yiwlaWprEL52O4QVpVyxEpmE4uR/yEO0dZmUmsqB8POzMgqIWsYMYvUFQm4pF5HEh8pz3mQLNPS11XDfezC81LhVtyH3NUNMfzIzEutDhEkUYq3ODsIryXpXQjDUU1X64ZyIXfjlYylanaEsvQZNUCZh4brCEV5Z7vusciJTt5UKoU71FnLKK/gIpwIRi0XcMhYLJekLSEwREeZx2BUSw0b6OgYpkUyFGE/CIRUy4399mOUVDa3m4T0yaOL+lYmjE1yY9TxxzVsv/Ndxe89A9qcHt/rempHErxBI2wGVMhSyst7lQdp6WnSsnEIJvsRsP/7BcOLjQK+ORGmAlbndj2Xgl7DEyhT890tweqMGtQ04EPdgsmmv2ksvxMLSnLTPAkZ7bVqNaxBuae6H7DIMXbuNOrlSxCIep0KIIyAFmblEbSMqqiQ7o4is25pSpzFFSYfgRD+LDuFz2BwRRGzTZ0ZbDLmGLDjlXIRAJkPlaWnZPIa+Ea2GTstVXUVBk6kkNF6Z/G10UMRjVYhwJFKN4kuzwoYJ8osgBUNUJsN4OvHnYUa0Ws+1I/ZbHIg+MSZsovq/ZOObepyKV/D66iPUaCFSI0z0JWFN77D0wVM8OtyKnLCMaBLt0/7j7kHrr7QaOn4auQRLJ/5LEgU0FFHxjYNrRkc/yJYeUHp6Lj80wVYLA5U8WtvKn7VmplZEyLlXIgiid48M9feRdhdFec9iPVfF3OCTiexS2GzMoVWTnBkY1vPgNotz/Wdqbw+JfyuJr2y7fVvgdP2qxi///c0rb8mWmy1otbwIc8qWc54wkfpDjp6tCwpY9ZSvgmfnw2aLV6wKtFGVPCLCvFsLA9ZvScFq4kozy6SL4cgWi9+GDWAWyA7XFmXFBi/xvvAZRaUIS1mqA8LfLpLfmyhPnjpyTiyr6iDAYKD0j7L9xrTAzllnF3SKLPbZEh1uQYaEuQdWeHmlD7od1jVigsz4NjT5RauCoOvgqb931aWnuc79teTZ3d9QL/yME1fTqZbTe9SoltJnm4zmXZEOVJksSHRKGh126wsEWfodSRpaOW1Wq1DC/PsH3qFsFzqbE2WVQpgbGzB57C1+T98dl4Z969ViDOwH20RGRDyb3stOuWZ0GMU5Hzx+9vkMAQQxbObcDnRrh4NERXdnLgyM+MDG4mABH1HrNPFM0Dhb7KfV3vMfWpu9O3UrXcXl4NjSeeG3c+gDr+9b6FBHPx5GVzwMtgj7SXRlJxYOGf2i0lqSep7/L9C5Sks4ydNGL073mml4KiQ6XSo7l9nbT7jp4+urXwVB6w3cUugIk79mm59xzGZi3MCIfRvaffXhSP6+OcNXmmy9by2vCFU5ck2Mc4KJtcuPN3Zwah+zd/+TYq/+qv/QYpcmcJzZ+zcvvE9CQVhNz5mznWqfF2QejL2LcQwNHd4RbZHz39Srhz+Nnf7qSRrZeueEEY5/esgI8IcQfIoPcNmbP3bVoc22pOfHV/ffGTDN8NCp3gzpSeHHNXtEU4NPzFC+7ekbunBnknuQAz3v0tjFB0pHbc0da6Zc9mSJ37yxW01e+/eQmE2U8NPmA/hZEfHT6fdHTVi95sS78XPNpWNxSNnjh1m4tpO6yPBaMI5E/mFoSZhzIGjR2vJRN8+MsyWVXd/p67Rmm81+/8HKRcfD1m7nj7h3alwXfPGZDZOGvXG5sXGAtrjgiMxwGCq8vcXnAntiSFy4JRXFK8nlK9U1BkfuuPv4pSikOHb2qLkqqz4EWEsMIgqNI0FomvviNYkTF2w8MHLXFL17W2bdU5mzdbytGr6z7Pjyi/YNnGY/W43lF5684/bXkr3a/XfUC1L27nIWxnJSe5UaCVOtVuQnzr8b6tn36S2/I8iMTQcnGkAVJOZXE/VzodhfXn6CGBNaUWU3u8UVWTmlkr9peRxRjWC0mt2MTuGTTz/KtenNrDHjLUg9uVll5N1zQ5j3V3UI3L/lnVuEuaRHZuA8fKWfXZd2ZHHuw8ge8/fOvOR0T9JSEbMfJSntiVl7YMbqZfGuh/avCPLeFZfBdWgvb3oVgkWpIftwPj+KTh2mjdp2YxQkyjg71SDyxwtQwhdHYolDI4uGqFxcPWH0geOP+s/rRpQtil8GxpKoNdZJ4VR0NNFlKcWSxgOWy+EheBJJVJZeDqvp0Alyi1B9IzIZKzMJvGbXgRq79z5JZ/dXbdhI9F9BEzhOnIZuKzMqDKEZ6nhZK4LYny6ni2hd82/cuQNxRFhx0ct8EbOdqWb5+QV7+sRN664rW+CAfxp+xsFjT7Hd1wTa65BhyG7odN9zk0POvyjs7SBRB0RURnGdvaiTGh5ynGu3+2JSYjKne+tbJ6+he5zzMFORPKs0C99hRsHb4pPYPXpJujyiMuVBM2a0o+Agy2Gt4bOp+VwIkjpOfv6rQoTZXaMhE1rC3Ftbn6KHrB9qK12rQrN3H9bx6LboV+zBHVPjktnG4/pWbplg9OxlTryUdK94oiVFTrgmiscuq4B4+UVsAUQl4Gma9UxGofEEIh5h41BS/0ckEr/nFmfgt8j75KTISVFE4xu3VTzCl5tK3Z3c+PVD0DVURZVmZvEkXRxZ539LvXDzU7MR+mCmTDcjrkh72WpV7KKu9Lo7KCJ2cTlEoMsbsMQazAs7YPNeaNrhx/1wMMPJzRqz8tT5gp4Tvg8eiiG+svd0NysKFrLsZQ7feZ1fGYzTGuhUvd6Uad53iMaxg2mFPIgAIXxsR+c+athreO4zKydbRrkOgZ/PqTnM9jMIVKE88CfROdTVbUBEhUqum93aqWChPg6t0XdSv/AhSGbfugnBMYyVuQ8LucL82/1HrC+ffihpQFkmB6ddOS6rcBGqIKh3UIUKvxRUQBBwnDVhOI2YtqZ6lRqSVeu0qKK4SAilXNm74I7UraJ0W+vgURTzGednFfcPX2qdN+fi0sEdwI6V/ze4X+5mQ7ouBipVNY/X6KKN5eVlFgogDemxurN11fYvHFObClUUlYi4n99mC8vf93dJqHEX09LqpZDqjp01KtvgaAIOFnO/rphB+KV8CE/ENWQugJ39NlVU/mTBgMM1Am0lvg9NVCNCBen5bEiHCgkLMrLZRKaeElpuOARpdPNe2mFZUNDI+BirsW5jlrha6v3qQg68gfvuKdc7Ru55o+Z23atDrRFnhcESSDiojCuUs/Hlt9QLwi/nQlgKTk5hiB0ndK7Ha0qBsWhIwObLXU2FJuvbd5YRzujoNoS4YPut3LEeWt/tn7pVb43KJrykLQKL2d80qCIrMeH8oUcpaQXZyTkQGhFXnsHqGmuSoCI0Cq/bRuL/OWgUJIDqcpyyRFdP+fSsOhtU5giDw6PFFXXfvWnAMdrRUBezCjOTrz4ViTkX73zqrZ5eQTajYyHppkOFi1AJRomIhVh8gaJbrVo0zb8WH4XFYSB0d9+Ia71/WDZv4b4qSSXEMSDU40D75KntwFsS/s9ARGJIjCDfzIFYYpHQWEz1mAXFgFalmgifJ4RwFCVY0ikQQ/pTXkWPNflxiIKVKlEyih5VlirDWGUsxJG4iYbkSJoD/TX79iw1+GkMhDzN0/ZguL+ryNkOm3b8Qpa99zIn6QRZGznhEKzcMTD8+ISH8WEnz8RsnRN12iMhYlZvZRlp1g/Czckukrqh8syP5SKHhuzcqPN2fA5bgCZR5Tmt31IvME4JD3ELubLtLkqllX4D2hl4uo4q9OxpFgcyVrBVQjb17kPrcSbh/aDveYYpTNVaORXmJ/rMDDyn6uTr2NeFzjnxZVN16wAFk5QrV2ZIV8Q0cIWGDNHVCUpFnfa7X1aBphgw8cWZmYkpH1u5D+aeu3Dqk3MhQm1T7TgVLUJVXAGLI8QQyYR/x2tCv8NxwiTdjnRR/NNUVu+OP3bVsfq9fNbFXx72+EMx0g70Of+/wKq2V4Huv04vRfTVJFVfkXknQ6ja0YiJgSqtKYypXMIHCfJuPsmF9Ue2J+K5rRnQ7efJZYgJo5auoL7G/wmcWns6lPtRkoo5uT4FI6q11oRu3/5Yihj8tIoBp2tu0Y74Gg0jEN0qMGyhhxkDV1d4JTCxtfXQLdZD5l+Yb7z+YtSbWb2tq05UvL95IuI5uq+H+8CaY7gwjMVAfA7/x44FUvgoavzpimELlxJ2rZ29+UKv9YMMsXXErxfe57e5CKN3jR6wiMOqQCuRqxdS/pZ6Iajqa0DFyelsxFzGc4/GkxtiDZT0utgonTx/9k5qj4EGMuyYqPD15cj7vG6uLr1Uf2oJES0H9NM/fS728/C1bfFfc4qGf84p7+XpyL2Cgbc2zLYjQcLs05ukc6ZVXdFvpZJROnbGza2nkzGWHr52WjUGo38S3Yh29Yy7ytPpOuA8j9+9LpnsOWWci9qvWXaspq4y5/7DfaX0kd6DBI8u7L3yiotXrxpHUbwIlfCyH+aKNXurN/cw8+/lN+z+JrWZ0Ftj16ltQXarl5hCH9J4Riat8NmPHwhbm4qfXEgVqFpq1WvUAP8axNYjezK3HI9cfl07qAv+weGwiHz9+R6mkqZVifQ0v7isgk9j3z4WHPBeeWSQgx4GK+rhahO9bU7oKYM5rtY0YfaHR/Hp2qOdDOtKBVa2tNISHb12q8R5ZH2Dfzht+ykm0XO2hW7XmOttQhMUfrhyL92or5M5iffhetxtxHjn0PETfthzIC8c4qQlnsrVd+5kQBMVfvhSwodUTVWrTyEF1yet3HkbgaI+a34JdmB8v4igq0cV3Lx6/kvXgeKURyWaPc1UMSX3F64/x+q2Irh/byz5Xrz/1qnnLc8P1sbJiV9/B4WXGX+/gGbWpW2VRRd+CZ82ajY0MyVyaGv499ULrGzcVwsJvvY837nP9xU60u0obLZALEb4LDarBIdXJsntF0tRtlw2tPXJfRv7rGFtcrM2IZU9f/yMYz3Kq2oJLS8lOHDduixILVcvZXHnn2bXCK36TdI7FHn+/bK25nXNEKNQSHnG0y8sc8rrzRtiP6MlffH69tkiBcc2+C95gUBnUludCPb4vvKVX1jC4dM4X0XXS1+qMUJ2eYWkxCyepGMv4nBYJRCaSCL94rh+RcrOPcePFEAJcKeUxQ3cE/oTOE09mvBIwj19zy26+lAfjYCYO2gNdya2jiLUAzfz3oUCsp2V7r81pvg7XptCsp28cXfpitmLR26UHOm439w1TSVxt/POV1wIorYbFuv9j+2NBTQEovWEoK2Fq+au9topsaT0jgvXBK4w/tZAT1vhPWCF5DlWNfdZGbGuh3SbL1rP7WhgidemcDv3cGkUmGHrOsu5t2Gd79nBt+vZt+2BIzvv5Q110ahH2bF60wOC8tZtnDnDbWZlApqmrltsepuT8IZ29m0OHPae4OItDSa3tnDesMhnqKa8cOTzvZMzI58WVd1WqY3XgoAFX/0ITNLv1gpzOwW2MNf+sQ1OshkxYVBS6LjRNyUH2j1XPmjb6VHEhj1sq91+vXTRaKjb9HC7+2O3bYy23DxNBysjfvs+WvWNGrJTLh/MornNN60WGufT5VTIcpqd3nfR/JZ6wesN7aOz5ujZc3k9J32tltJnG1vNu1os/RltNTgaMvRL2TmszlfKETqN3XBauGnBmUiPa9I1qSgVUz+9QWMNKre9YjX69el8/Cq/f3c9GSYbpyvd0Ln/XNJk8z5yl7fgTVy8Rl1e4zvZxRdSdRw/cwl31WpRfZ4TJrUzb4V7kYI2NDf86gDRRIYe6eZKH5eVkkyrdZy+KiqwUnRQ2Z0hQ1ZcrR6x/jB0uIvEPvrv2btKs+405EBs6+NuvGPnu/y0XPYvrsSByepaFOiNqn03IxwOZd+3zd497yjaEscptwj1UJF85UoKrccO039oYZCUxjlOmk1gaWLNAFjLZafYper3wAeJA6uDiQaTlh+YsLAslw0zqGRpM3JMZLl7Sb6ApK5cZ6MS8O8Ck419Aw5NW1SYySHqMEg/PoRGoXs3jVZXVv9hjTtWr5v3tW4TWfnZ2QhVT025etak87KC69/iKLsFX6s5dUZoPWSN/clhu/cl2i/oU98EIY7ZbW3YmdWc/E+FiKq6Gr1q+FKQdfzg5dIu067PsGOi+Dkf7oRs3TNha8feqwzPygxf28N0ZHi+Oys7r7AMTdNn0n4YeCSZrt8dP68MxaD9POmDN3A7c9w5v6BEpMSQFFxydtDS0+KlX09jmJ7rLnrWGb8ehNmHd57OMfNZ3KHaV7DTHyWjLFbaMWuagd9SL3hzN2/3U/4r9iW7L7CsWohEtfIvSvSvtxA/gGUO8t48yBvhFOeXYuhMSg0hwMo9J4e9nyzvSoyB/RDbyG0RyTP6dFPuvfTc91lwZftLCdVGDafZ79Bh+9C8UlhFXU1SqokOfpXhaw5drvxLDT0aV/mj056Tp79eT7KZGl00ogyl/L3eKRazX1yYjfBYxSIio+aL8pR7Xrl2U1b2LPfF3fh2QLcP5t2QFetn8EZduujvfCcy1/u1+XQJ1C4rixNXVh+09nqb6FX9W14R6kSYfXXJ6aJuUz17/GvbDn/jizphnLJmjbEkNJGm8W8NewN+AUlLVl+GGqCwRJo6WWaLFkNR01Wg+YpWHTR1Ss8JoZOietyfa1ff+3IqEyCpta3RSRHm3Ay5Kx4cNtihlTS0vYEG+8bh+Ny8wi9fZIaXiiBJUxzGUbR1KNoyE4CJavK6Y2iCGlOj4YVTJL4g9erWRc81FkQOaFvt9Xgf7j2Ces4cqiFDKM1dL2hGtw2TLTqErV/UY0ekXSNfHAaTVJiKjgSi1Wx9u+5d/yKD3a3O1++hiUxNRe0UrESTUcEwnsKoHdp0cLOT1m498YnpcnaUcTONiypWBEH2oW1RtzVG3Rug25I+ydMktJQ3XAMAzQVOx/Xg8jc2/qu8TGLiXBT+pBRMVFFDF126cOuxjkMnBpR5/+iaxyiHqV11ya9lhjfTFzYaCTflyIiQZ5a+EUuNv7kBtKbDsgQNY5W6rms+sEau/gfe+AxdvdZm7/qJv/9LXzBjxPoTI353qs0GJ3neorAXplNuBbp1axEfI+G9OBow7ZlxyHZPy3+wgwQcJ+DfB6Pdc+6VlWYZHX5lrSGs2nv3kpcjQtZYXViDhiGE3HbspE0hg3QJaA2Z4S2zcY1T7+I7u5NL/5pvuscw25gw/1yWIIyax9yQo2Z53X9xCSigBiSLrTFH4BY074XVtXLf1tF2fANf4v+XATQW0MKoNXHeJBDa9R7U7hevxbbqM+9BL7/iwoJSjIquyreNe/LCWyIwpd3YAY26Q7PUC0F/+CD9pr7p/yktyWtKgGnt+k3405loNoDjBAAaAoxTUdOSMaopLxwAAPyzAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACAMcJAAAAAIACNIXjFHJy36QWodUN2qkSW9brEgH/ZyCs11sOvu85blAn0h/VRGHB+YMnS/t6jdJu8CvfRaxXj+4kfOSa9x/YiwHas40CYb3de/YZomsx2K69OpAloOlppFYJC+KjA8Yeel753XY9/+joVUb/5LvwAS0JBIJkukV+5t51CxdlOl8ZUyOQ83SK19zDqjOfb3FrXbe2c5LnzAnJGLb5aF81RV7XzrmxcbxTgmrY3sjpWt9yUvj47pFVlytUt/s6NuQbT0jpxRBvlwuQvX0fPcdfyvyvxZd/o9qFYiVv7RuaN3tTwChZ4mE93Wg+76qWX8xNN63GpdwURUYqslIfHN4XsaTriqcBjrrAdwKamEaplCjnVpjnofTesyO39NUo/fxFSU+O1+Rlnz916pmZ11KzZvrAKuD/hNLz62b48aY/DrCr9aVgwfu4tX5PDDdFTban1PCrKBwJEbHFxPq/Wi+qyEj//IklVDBLKAIBEXDF5Jq6TzJesnrpyymrR4R2fO3fU9aHon8AKU5af5nlvvrQ0e60H5oEDc/8r8WXf6PahRJV5L39nFUkRzwwDi8SccVEfKNTboIiw9ROK5Z1mum8od38wydye83WBp4T0LQ0rnH4OOFhic7IABdTbRyk3UHut8FFxUkrIo+SV45Z2pjUAABEkJuakcuAxLXOiApuLtrzxmjUbu+fvv+HJjLwEIGi1GwjIWiyMh7CUZR/HJTFMHuF+F1pH7Q1yM1yW0dy3bfgF2dmIeqDDcg/d6QVzXyTFVZ2oeoAQ6SSIJyKUqO/Rtp0RabomelBSe8K+RBwnIAmplEahcLh0BArK4sHmdd8Xjgp0TuiIp8Wq3XyCJnm3Kb4snfQkReQGI5e2D3edLX/ZLW7O+Yff5iK0nabsmSNNb0lf8UQ0MwgvLLc91nlRKZuKxXCD5qA8POzMgqIWsaMqolzIae8go9wKhCxWMQtY7FQEv2TWGtilQbzX8ftPQPZnx7civBTChLDSoRJlJ9n3xFeaXpmdiFaxUiHSf3+FKAkt4VEnC+ZeSI1XT3Sz7opZOW8LxTR1TU0vp9Ck6kkNF6ZjPo5YW1773l6E9bsSVwU6qJbp5YjIoEQQuPQP99CwczLja84cgpVLZ78D3mIti6TUqNQGKIyGcbTibWKoHDKdRRBWJKTmSWi6GkwyOj648NoLBoSCZDG5ggAqEWjHCfZxt3FKOHohPXt4pe4dapqLovyj6yd7Zvefa2H4enIdUNIBo9GG/Sza3/5ZTbewmF0e13Gp92D1l9pNXT8NHIJlt6iv/0LaF4EWbHBS7wvfEZRKcJSluqA8LeLOlGkJ0R5z2I9V8Xc4JOJ7FLYbMyhVZOc8clTR86JZVVdGWAwUPpH2X5jWqCNdMyWn3HiajrVcnoPWi37iWZO2XLOEyZSv4WIiuK3LBxz+n2pxFWJ+CJq51Vrg5abVakvjOE9nDYxdFeqCIIYQ+aGHhxsUDm7gJS8O+u3NjI2taLyFmpem2L2dqVUJaA3cEuhI0yu3avE6w511A+IuXi92Hmcap2+DBEhEKq231Qw87Li/yJyCgWjKx4GW4SdeyURD717ZKi/jwHha8quiXFOMLGevnUDUpZVBIT1+GzY+Kgrr6rF73xx75J+FPnxq0DBaJRYCBwnoOlp3BgGxWzS2YV5ThvDu/qlHVnn66GB42deWXsX7RniN6cjbJ9zvevVq6/H+w3tY7Fx53Wy1YDpvZU+Ht2dRrbeOWGEY6MfMcBfTeG9LT4X2BND4sItqSheSS5fqcoSCnMujV18oHTU1tyxZsplT5b4zRu71eS1v93u45eikOLY2aPmqqz6EGAtMZQoNK5qzhwpe3c5C2M5qb2sD0rDOBL5hwFENNnEevhhdzsnfbK46OECv3mrtlzyjPBoLY0renM0hjg4JNNN+UzQjBmROy/YB3mowPwvZ919Q56aTbywdnhfpij11ati/e+z9TCWRMXKLCKuVVc7g+jz19K541TrmN0X5n96n0/Q1FOq3YxscOYxcuL/KjILBYtSQ/bhfIJPzFC+7ekbunBnknuQgzpcfQGZLFsKiqZcqwiClLjlPUI/2E3YdGa4pb4o594rVjtSHfG/glNtp1ye9DKb29nw53EIAKBRNHbwn9DeZUUSleq0/PTQOXDCjpnmnx68E5H75z+NuwOVidBI0ecvfMiqRnrMdqaa5ecX7OkTN627bpM8aIC/EoTHLquAePlFbAFEJeBpmtWTVMK0WyevoXuc8zBTkVhkmoXvMKPgbfFJ7B6DKEQ8wsahpP6SSCQq1bgXNz81G6EPZjbQPOJa2Tm1qvpJNx/dXSPsSmq2AJI6TgRiKbluHd1JGweNGW634kHSiY8cjy7YF+cOX4etY5eO7V+5oNTIwqaBhSSpG2pDpR8LeZKfMiPwMuImBe07m0EeNmOuA6URmf8ts3gIVKE8cPaiTmp4yHGu3e6LSYnJHIdmbwHzPu069BS2Xr5vrLW2VPw6PRoofpLJkunOw8KmGlzvOm/Z2gVGzZpLwP8VTfC8YbS7z7q2VmC55NTiyx6H0Cw+9OVgTMRZ6bgTyri12k+zHhTzGednFfcPX2qdN+fi0sEd/ux+O8AfA9bo5r20w7KgoJHxMVZj3cYscbWsXJTN/fw2W1j+vr9LQo3IpqWCuu6F8Mu5EJaCa7AuIRWfn13dc/Xx89z8zx9zIFgs/rrcSNfa2rCy/0Kga6tCFTnlIgjhvniWDRmM68VQfGIBQ5B0w4r4Qnk7aNAk7a4WZu8yExNfZrD669eaVFUs882PurO1dmULB8fUpkIVRSWiZk8SKU9JzIFMx3XWVFT8CC/97at3qFauVh1MGtQoAQAaSNM0VNHMzoPHaMTveJ4hsEZD6A4h28NH1NguIGLXiAuTLNxXJamEOAaEehxonzy1Hdih8v8JrNwxMPz4hIfxYSfPxGydE3XaIyFiVm9lSCz5pz/lVfRYkwYPSMA4JTzELeQ2zIoL808G+425p+bp7jjKls5K/OL9+PtJugatatxPJODzIZwKAYbE/HKJ20YJhYr7J0TAKROiKUpyXTqG0Xnm9M5jOiwzWnX85tTuw2ptslEo880PxYBWZTIQPk8I4ShKzd/uFfMreNJRYpHC4me/2HI+y27+0YN96KB5DmhSmmqER1ieWwGRVSh0HSMN0b0baZwRtO8OEYXGSMyPSPRtmh6r38tnXfzlYY8/FCPtQJ/z/xeY2Np66BbrIfMvzDdefzHqzaze1nid1gzo9vPkMsSEUUszYBiLgfgc/k8LPgiq+hpQcXI6GzGvX5u4n08tvCCYsm3DFjMSJMyKOlwqCfxmlGFM5cpRSJCR/DgdpT9PnwihIQMNIvTo/v0SV73aWaqTiuy36WLGCOb3vRIiLqscplB/nJQjquqoII/yKkRQfW9LqDvz8uE8j9+9LpnsOWWci1pjnvlv4sm7+SQX1h/RjljPBeUp55bHJtOcvJfb/mLCaLKmARG6mvQ6fyBTQyHxC8tzeMT2dAIwMICmplGOk/vy4tlHKqYdlVm3ToYfYLVe4dKGqYMaqXFu+9Z9A1d72kKZb3g6Nq0oaAJdEw8l3b3/orO9fsWbJ8LWpuInF1IFqpZatXauAf5f4KQlnsrVd+5kQBMVfvhSwodUTVUlwVjDHq420dvmhJ4ymONqTRNmf3gUn6492smwciqNoKtHFdy8ev5L14HilEclmj3NVHHSzqtxXy0k+NrzfOc+zPo1CoUSl7/78KW4NeXBkY3rsiW+Cvnme7ilJWUCGuvFsWl73zP6rBnGlDwhSt0GOTBvXZi27gBpxsBudN6HFy9zWjm41v86Pd6HpKQvZDNHnarJV2HKMR+jbVD44d0ztX6MiGr4Lo66Mi+XipSde44fKYAS4E4pizs1YtiSX1jC4dM4t48FB7xXHhnUS78eA1Lx/Oye8GsF0GPY4cgSh18bXFIyn9pT5dTFYK9YfLCLuQY/886LIlOHboYNWwSlgGgBgIbSGMcpKn1+58iEmwWSnzDdYrb/4sVtJQbCLGjDwgL/rQNHHZaEt3Hb+ni2BUXJfJaz7rnTazu8fHtw4LtJe15xIYjablisd8dGr5sH/KXwPt87OTPyaVHVkVIbrwUBCwylP3F6bkcDS7w2hdu5h0uPYYat6yzn3oZkqa6SbEZMGJQUOm70TcmBds+VD9r30ZL4Drze0D46a46ePZfXc5JGPTpNMHDx73N5XNgkehikbTU+zLNi9D6RdJAXTdRikk7tnUrfK8mEusOQ1fcm9WBKe4CwitWsKwvREyKiB3pFV95Cf/ySzgO0VevpHlakxF7JUu+xwLbaU3FePEpFtZ02UP1XZVZH5uuG2NbH3XjHznf5ablsCPo1x4kmMvRIN1f6uKyUZEOt4/RVUYE96t2ETew82MMqbsej0rT0CnkLpOoDpjjOColGr5sfvdisUvxK+v1jOtsY1id+AKDZaIzjRDNHB54cyS3L4+HUqd/HQ5QMBh7YP2B3WVEpTFUlY6XhsHKfOQc4E4tYOBU1InrE8JJ8AUldueFrOQD/HnjTkeH57qzsvMIyNE2fSasxxorV6+Z9rdtEVn52NkLVU1OuOdaGN3A7c9w5v6BEpMRQr9KuymBzN2/3U/4r9iW7L7BUqVuxsFpj/Y+4++YVwCq6NMm9Jw31qDphsSXm4haEV8wSUag/vvENJpm7LHzkMo9TXFAAUTSopAborjA1YUdkkdn6MR2qW4cVaVc/onp4davdS8PgSXiIX8ZDJA9VPXeVm/m6wRt16aK/853IXE+5IdFlQbGY/eLCbITHKhYRGQ1+px9Bu4sTc8cjxLydUv2R5QGTDCcu3D1xHjevoBSi0FVJ2IaYDhGPw4dwZCzocgKanEbPccIEZQ0ZuwBgvLKq+k8RqapVEdFEmkZ9UyOA/wdgHEVbh6It+ySGoqYru2+EJqgxNX4OY3TbMNmiQ9j6RT12RNrV2xNCK9E1ZVtyGK8idxgETVJh6tVz52r42VfnRD03GBk18eumK27mvatQz3AHGW+uxdEN2xNiTtxO9dNr04DJC/mZlwM3O2nt1hOfmC5nRxk3ci0ejKfIfbVmbXjZF2K3bMliTlo32rLxWynRBPWG7jiSwH13J+ENRnc2E3x2AtDkgJc4Av4RsEau/gfe+AxdvdZm7/qJmn9Us3kpwQHBN4x973gaf/NwGEavfaEaVjLbAspWQZNtncImqfxnsX5L8DyDJnmHwVc4yfMWhb0wnXIr0K1bQz7V0nQJ34pY6PfJbM22oBnmvzVhUd6lIT7rzxVS+k/bPKTudzYBAL8CcJyAfwaMmsfckKNmed0btXC0KcCqO7rPcbDtb1Kjt4Oht7Gmy7sAb+K2Jq1fwYfMUiVmU2eeZLE15gj8B9wHqcesfR//RMJoWpf162N26upognd6ApqFP21hAICmhKA/fJD+n86EdD2LVb8Bil6EJqm2a6vaLNn5U52uP5Uwjm7aVm4jBQBoNMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAMBxAgAAAACgAE3iOBHul8+fSulGJiqyPofESdl38i5k6zHesJGfAgT8Y4jYxblpxSKauqYWWWFFLE+5sPUeNNDd2RyoFQAA+K001nEirLdHRiyJulAk+Y01dV1xYbaD7o/3RDhvtu/ahaI7jzUkgS/jAb5SfilgeP/r5VUH2p1Hb188aTAT2+DLkbK3p5buQmk49zMHagUAAH4rjXScnFfLV0YlqI+7EOHOvLu215b1My3NT/RiwLzs86dOPTPzWmrW4roD3Ox72099tPUaa9fisvZ/hRgRIZCW59OYSQbpZ8fPDh0T0vrdWiftlvj9RF7qvVPbP5r6jzWX+RXqJkSUfbb35NBnulPubRltgoMg1r0Rk3cbB0asbouv/2IAAPCbaJzjLHpyZG+O+rQVY/prEiHXaXNOTgg6kfTF3kWrOGlF5FHyyjFLmyibTYcoNyl6/n/Eo2PG/umcAKpA09r0W9hn/9lr999UOGmT/3R2aiMqPh8dEUIMWNz8KiOGBGXlorI3J3d/dAsxIUKQsLy8nCMSN3vCAABAARrlODmvkl6zyB366xOlRzjNnubUgJtJyZ+xK0OPvIDEcPTC7vGmAX6tJSdFRUkrVpw/k47uPmpBSH+9ys4e50V81KLTT/Nonf1mTBtvQBDmJvhsTrIa3S3r5KlUx4AYe5WvY3BI8Zu4VYeu3sgQdRy2ZIeLNvdD3ILIs7fKlO2H+AYPMCTDwvSE4Kn3jRfZFW47nT1m5VI3/OfoHVGRT4vVOnmETHNuT6i6jzD18ibPIymSrK1YNH236cgZ8Nmt5f2j5/XVx0jvMDmBGbSkf0rE5vOGg21TT+x6xW/v6LNtZAc6LCO3EMJ5cWnH/OMPU1HablOWrLGmt8TO0t+BsKi4AlLWVK0cqUXKP+yKjNjxvIxhMSRkukvVSGytwJ/u8HPt8PNur4k4evZDIaJq6jXFd6YZFS3KPxayMb7tcIf049sf5FI6j46c5mQsrcaU/Tsiwh9lo7Tt1y6e0v+nahRmx24O3PwJQuDdLjPO2Yx0Q589UdpvcVRfDYww90jwhiPMyTH9s+YH3+sw2OzVibh7fH3PqXPmd1CuVJmUn5SwnrSqwNItKXkHTr30N+lCq31WUPYps5Skqa1BqH44hNxyNkKgkqDSnLTPAkZ7bRq+xtA1wi/5lFGipKWnSQQD2gBAU9Eox1mR+qkQYhjpV7slnJ6RGnQhOw3S62fX/vLLbLyFw+j2unq4Esm5x7H/GQzpZV94ODI4xLZz8Hh16EvCmt5h6YOneHS4FTlhGdEk2qeToODBg6vn3ibwGNYzaZhvDzrr9V5Hv30Z5oOn9VZR0aWisi+M8At+ZTV+ptHztZtmFpH3H3Gg8gveXLp692GCQNPaQw1VeGTtbN/07ms9DE9HrhtCMng6tX2lpUVRDbq6mjy8k4O1d3DsqqOr+ykn4fTFh1P76tMqniVcu1YwTR0vuPnmQeyV1097DB6on7h5x0KORuyJ3io5tXLb/uPuQeuvtBo6fhq5BEsnAq/5a4gFRY+uRs26g3Vb6GKGlzqqmABfn1SrFR5Gt2M3OZRRXq100BDXDrSvcQ+RDF2CxCidHrPt0A+ORcxdBpvHLulLEuS8vb/v4qsHdq7DO5ZsOr1hmrHFlQGUB9FLJl7VnDVuCLUEo1G7GlFk067drB++/IztOLRv+7Y66s9znkRcfLuur4ZaxYfD159k+agQBcn3H1yJff3BbZBd+5tHFi3i6ccGjqAV1VJC/eS606oCo+7qSAk4c/zyNMvhWAj1vZTFNw6uGR39IFt6QOnpufzQBFstDOdmyCjXXK9wrVPTz6cLIIhhM+d2oFs7nDR+4sHAkTFPuWR8WSlsN9r/v0k2mmAVPQDQBDTmQRJyC7kQhKeSqy0ARklZYvlYJZjWPn0sNu68TrYaML03FSk4Jzmn57p4v48J9Lo8flp8XApnvErRwdi7GMfQ0OEd0RY5/029eviTV2c6DguJCjSnPd82yuTb+lxR7rGo2Mcang/XeVtJe7b8l/sOX4K6HZ83wYOSQ3g6cs5/dzN7DMDiMGJRaatpMbdHGqDSDk2/i/YM8ZvTEbbPud716tUX49tbS707WqWtw8gOhxdfJzo6uw2nQhy6tV50wpU0zlBC1t0UvmE/c000miCRCa3froVTbVE9xW+8Q049zO1mUiu3Y6e/epJGtt45YYRjCxxd/FvIiu3sEiv5227ImvA+UqvOS7+06SE0aPX8gJ6UVNxTo21H4/J7jOPUDuzm8u0mgszautTFpEfAZOnJwdQXhxY+vpDJ7WuMlboqlf57lk6zQb0uS/KJeZxR7qRx70kOzXpBwIguVJk5RFM69ezT49CO/4hWE9x6MyAu01p9RcLDtxwHpayXL/haY80Z/2vvvAOaSLoAPtn0kJAGJPQO0lFAFHvjRFFQ7O3ECor1FBVPxd6xiwV7907x7N1PPBBExEKxIUiVXhLSN/mSABJIaCfntf3xB9ndKW/evJk3Mzu7i8HI7Rbo/RAaNdNRbjKJMy/uTyz3s7u3oZERThjWQl41yD1+zyFuFyN3PfkyvC+6bvwo/nQjfPCx4omrz27rSnr965qBh8KDLc9G95U3CZTo0/kN+JFx1/1ZCaud157c/W7YfifJ57vrhpyqXrz76nJHUumLQz0XrVvgcOpsdzoy8URA+Ga+aQSKghTjYams7haMTCr/BWFQKPWgLDM9ueeSUtl0ICwTykD1p7vZMK1z8f9iYwEPxsrKUopFgKmI6Tigp43qUy3V7y6lw9Zj+joSa455qcl5wMCvIwUCGLq7ow587+VH/iBrRX9gPqGHkdx1F3969g4mDyxOvhYLqmC0tCwzTwQAQUMBSGZefai//J5SJDDIiCml9nTTx4MqjFwIHRtzRXZG/R3IW16mZZYR1KSFWR0c9Lk3Fx/tdy24u3Hrd4MiqMIKuL35B0lS9LLI5V25axKW9cZlJX8EBkHWitpl2ToaSO/F5PH9KzWcrHecGm1JXt/issS4J/cS84SAl8+RyM1VYV4Mc2O5iUhpphTAKeXCGIa7A7P85v6VfTdt7c7S9DRVIwj2Xp10fnkdWyS0yHiVT3Xtp48DVWi59RnY6GvJrxu5dyGfe5xW8AWvZoRwK/OSyXR7zXE9OPny/Xc9rWtbkyjnzC/J2O7r1/Y0IkPAa8SskOvTIm6+Ke3bWV4YSZXWjFnD3ClY4NbHCYpNK5YPaguvXHqB6bFprqNcaUDXZfh8q/MLb6RWdu9O/+ZKQ0D4z/MtjhNDYBJRoLKKC8sH5vJjSXWVfAZK1CGhAdw4bK0zhZSuFshgfnmZBGTcO7Y4VnECZWxhhK91tyQqUVUouLqkQO5SjRi1jg/mFXNhFJFOUQRCa9OIgF9RKa25JpcHo4hRwRGBvDPH919Vpm1roUvU4MprMrPydyCeT3yfa5ucge8QakaSz5iVcqKVA3OMNp0EhFUVPA3SUpxm35xXPnBXmGfRgtthfs7IQxF/ADSRZdDB1XyxHTqnw87DUeN6TKrgSgBRj6SoXYwWjQz4RVwxV8NJ6dc0NNqSpPDh9IVrzwqte5uKZYpNN3WgamoW1BoiIHWftXVP2aI5y4Ny5m876WdJbqkaKZY9uhIf3P1Q7P4yj9hhnMNXk4FqTEaLRQS8Km6VBiNsXV4yqQQw/UZ0pS6/euTTPEzNco4gL64AGA82q50w4tkehlhhUW6puLPiUM+9L1s5dkPjiJCsWqbYO574BS7/sJj2QCVlh2pRayoFAQGhBb5pxkkwNWeAe+8+CYFyZVWQ+a4IUHtYakGgqoWYKCwOA9DdQ/Y/7Fu/AQIurL3YMCRB3iUIOAJJjbAonNwvyyQCsbznhGQioQRgiYSvMZSdFA6HBmjniH27RmvYXNEISudeNlBkwqNX73kmozrVL7rWzKKlInm2GCIRp0FaOS7DV8fTIwaE7wg4ZfdqZgfk8ZY/CoZt52QIol98QU3HyytZwpMoa1csEgMsGQfhNZysNxINtiQtu7hs8yncpPjDgY75UU5TLzeTN0SyCll9gBWxcNTOn9fZHdvUQdPShCoUuwBrVGh8cswHYYdRNvUGUWsy4moY4Ig4gmYjbE1eMokUpdspYCRj3vlbmV1qh5xSWCZ3qdKv4wWZPDs0FqO8CFFYOo0bsuK63bSTLyeatWIajYCA0Ca+yXGS7D3tKVfTb2byfJ1JQJB7P4WrZddVPgZHVWMg+bQSljYVEyIZuzLgG8lZnL6uzT8bB2kZuzHBycR3pcMNWJAipqUFHSS8+yTwNSAJMjNKgZ6vWYP+B9I2smLDT//3mTeapu7LUBgsSi6apFY0SM+xhy3vwrmH1RaDndny0X3NXLm6tEIMWBDnfWY50LU2ozUlLda0T9DGG3dHJn0ol3ZA5px/FGll7sdCQDahQtpaFiwQ/zxfMFWHVF3wsQDoTdUnaRPVTxJAWW1kDbYkLIjL4LO7e9iR5I5MKG4xfyx7ZNCMH+6tfPCRI+1AgGBBBR/SlnvsmqsotPyXTArXLqNAtG49Taou3L9QrT/VifHVZKpKuSLAQHNzUsqBkZW+XlNG2HxeoMblyWfCdjMH6kdF30tHA8WudKyOndzq07Irpaa68qD83NgciY6rFQsDshW3TNBQozUVvK4TE/z25mOp1EwfMUsEhHbm23bZMTqNnswKiYyIdJ/vo/t8964velPC3HXlFwgMfTyIj0t406mnrcaYJOvAvuzD0XvXea1Z5gA+fBZa2ZtrawxJtA70Noo8tzskmrams7YIb9jJu5v+zfubH/hbWCVsT4I7BvawxIJClRhk60Fj2Nf37Tnhu2ZCV5CbLjTqYk6p28IIkehMEki9lpDRt6cpm4TB6LoN1du7JtfwZw92/dg867cdcV7z0b9tSYXcZ3sYUXTUpcUXJD2TWDjIXtzKEuu4GbS4xIegAVjI4ZakvLi1ZHeiuENQsA0gS7yHMm6cO/tgloHV7QtJYusp/gZYsp6GkyC1LhF1W7KlW9FRBW8SX5UySm/HfAayzrKmHoUUfHyRLjY3l75ISBNT+xkQpXm/dB63B8w5Hz/CoLZKIQKLiZelxt7O6DTMlEnBYIw6dTPee+K94SRvdv3N7dTfLl73Gom5evYpZBvhoUvTUTdCbGaLedVDcB7o53L2wCvAUtzNJVqM6cXa/Wvkz48M13ngn53bub/YdFGAAwU0MTbFGg4bYr9y757Z0ez9Q+x1JaXJz5++New/AXntJQJCO/CN29NJjmtXB2WtPjp13m8AZzhs9vpNTsrlTi2neT7G169scE75ELfTXGPMrtO2RFWumL90zBb5kdHwmMPzvTTnQfCYvOlk5crZu+f9CrDu0w49GRd0ITDXb1ugIUBZ9l98NcAM3+ieKslx3ebQkpV7fMeekx9ZD9uTNN/l60yR6jQy0Dhu38bAuI8H0kPsSXiWlzUZCDwHGam8nEXXOGX7JLtKYNjzp8tDTOQOVU3aYPrjKJ9DqQJ5gh1Gnp7h2tw+SQQNKKZJoPCXnsN/AUSdzr3nPQ7yUyz445w3hU/5ELbVOQBABv0PbQxo6mR+fVLqtjR3bNCIw4uPdRt+0rafjwv6bqWgCccpzL8UtXhpqkhusp1HrNjgQq6KS0wFNlu99FRahla3EYNs46J/nJLyMvJ0hD2BwHLsRAY8zy7WKiZjbPIp6MeJxUBn+E/rZ5jIHaqaEQZTWpFXPTijviHOh6e/rjkiegau21O6euGayYfkrpzhGrp+7QpbAgC8JtSLtfVffal8w/Tds/R3K47RDIcZ8zzHWJKQB1IQEL6Zb21GENVu3NXzoypLORgaXevrk2mQdr8Fp3hTyjg4ui4R/eyxb+1p/YDkxwG1YYhmU38+FRhaVVgNManKtSqS//PH/hoyIZhMXHJ8/AJOuYTIVDb8HpN3F48u+yIi61Nr1rjQJn5RMr/6GFpmvqdODoqqKquEqDpkrOpwHtJ223vy3upyPoGmXEQT5Dx8yzPt4+1MVAmk531pd7iMi9Gj1T1nri7t+Eju8IpiMUlPG4fMNtsO+Yfwm5JlPK4MRyWoWiGa4TL50dXRhWUiGpNa9yy/hpMGgw/Jvu6sVa8dtznJtyYW8In6NDy0MrQm1NSDMVNrfkEGc47EzFH+XLL/TkhFhZBEZyii8eOef4ScA4ewVEWCGG4L0u5OKeTj5PYgP+blvEjksUYNsNRSCWQ0YF3MKlk5hq5bZzLqRthiXhh5A7lX10DQ7Gl7Hk37KgTZNiT8bPCS0lwe0YhJqmtqpL5h1yVf42v3vPPgce1vLGvIjF1fpvDyCkphqp6RNh6xUgSEdqJ9xp8YKlN9lztEoOq0tNECQDht/dbtXoBwFKZKSDSRYUhsOrQyBl5bR6+JK0ymcrIg5cSf276zxH6bn7VWwyAoDJmltreokbRoIo3dggwIzYHGk5p4epLI0lXTrMaTKjSqHQhPM2zVG17RWjRmbe0Lc28kgYC5vU3VXk4A4an6tSaTuiXilzz72UHWjYSRmwxDVz1eAyNsVV7NyUpkmrbJ5DAkQ2NkeRYBoX35Ty/cCFMvLOl9PMtj5sGpyJOYCHLQzJFhO81sm96vJszcvnTu6qwOmw8MtvlGk2kxLwQEhL8p/2nHidWzcA6cPXvDCJUtEygtD78payBLrWbiIfxbwTBc7RnNBcDSnZwHRcyaMc+yfjEFpWUXFDgFbdni8kob80JAQPib8p92nJCuZ1CkZ6NzZDffyW5/jTwIf3sg2sCZPw1sdI5sO22y5s3jCAgI/0b+044TAQEBAQGhrSCOEwEBAQEBoQ0gjhMBAQEBAaENII4TAQEBAQGhDSCOEwEBAQEBoQ0gjhMBAQEBAaENII4TAQEBAQGhDSCOEwEBAQEBoQ0gjhMBAQEBAaENII4TAQEBAQGhDSCOEwEBAQEBoQ18s+OE+eXZhRVSbbYZg9iW7yMh/MeR8soKC/jS2iMUTo+lS/nXG5Ck5OG1Wyls76CuLI0f0+Nm3NrzFPgO93Fqp0+BtXuCzQFXxt24+cnRf4IFEQB+EaGwGGibCRjf+L0EKVSWjRNrC1lUqOQzFqYLWfTar5KLSvElVTK6qYio6VOj7SUAL59QAUt0jSU1X8ORCjFFeRgMS6CjMVkYKs8mVEjFbDPxN/WHMFpzYY0l/NwabVS8OXKrwMvP2xH5suFfwLc5zspn4WaLH1bUpGTQfU3o4tCO9H9U7wcX/L5z9C/YsNUhA2nIh36/J9WPdwQOiuHVHdoe/vXwNLWvWf5B4JLfdobvxE28ONtT929Vq5Lim+cOn3Z3mqLZcUqr3kaHHUaxfX5wIrWL3O2eYHNwUo6MOVS87cQogE4Y47n4Qk3fIjPwz1pyMKej5i/jtoIq6g4Xpw8hSSdCsZEezgmDX188WaEcBWDiJnisTCmIfJvh0NiHtaMA6LTQjgtvl+3IfOem/AIc53qHCSO0hjxNnNdF2jhsJT3czKmuP+R3X/N+cWjlH+wPuRTNhY0vO1+jjfUiKvfh4gkiq4RJFq367CxCe/JtjlMmhaVAP/TAkWWUlB2bVoSt2GV3coU/4x/kOmVCTmluMbZSLB/XCbOeRu/76LByopPqNxIFBU/3RX/sOnmiF/I94HZHb/itiDF2WMWMU+cbP7ElLLgZHf3ScXKYIwnIxOVlxblYrkjWPmIitIy0/NaZO3CfbYOZ8uYvkwBgnnMgOVs7zmjjCPOf5/FOnS5tuV8Q4J/uM/jYNXuiF6zhKoXn4Si7l0gpElWYyYcdPOKbVIjoXm6iaebXfgLAZt7V6DOU1ByUm73cnKC830kiMsfdVs1rKnIFyv4w+cgyccoO2xVh9rvsnq/wF7eULargpkH0S87ksKr6LqblwmKNJoxzDt/1a/yI0F5I1/S9aYd7nCgMBksz6hIa5Ht09vWjaTz/7v+gb/NizHw2fPJR/oSLbx7ZH0EMXzpRNQBcGH9k0UXihfETNcZH+CYwJLYe27Q9BsxwefyKyAvkVePDFMnqT15/YXI7pIrQWqTlzyOTScN3Wn3t2SEZFg8b+eQET2PPimKnVZV2p7eQBlzIOLLIiHghR3Nbg8S2/flgHS2jIsdMD8AlWim5MtPl1U06jXYSQNutwgCYvHiDmWQvBjD2Yxwe2OVYajeZCAojxdIEXUI/+R7teP0ohedf1kJ/COPiV1heIKcpTbfFwtYXF9Lr6Nubv+lA2qxe7uQWSobQzrTf5iA8jU0HwnKBKPvB5pkJtku8SvdeKRi/KswPm3E4cv/B11VMF/+IWYNrloyknLQ9u/cfzST0HuqNiX1InLhyXQfO+e1bb3UYP6Tk8v4vA05OhQ4fuHD1Q6lUx2Hy9JC5jlQ0XPxLxJYbtqP6ZF/al1ii5z4mYoLhnUOHjqZwTPrMPDjJg/21LHDplZ1rI/GTL4a4UoWZezbtjnOce8yffE0e3WZU7+xf9z0rpHQaFxnsbUuQlibsHnMRLFo+uvjQ2m2fgBSKGjz7epepq3d2kpu7JOvu1gnnM4AMWrFkVpTDmNnQ1T3cgUd+6m+KkWQ/2D7tAWvdsoEZ+7fdtPTrmnXpcKrIbkDQ3jHODEUReW9uHFhyJbmI1mnO7OAfzQhAyntz5+CiXxOzUIbDpi9b7/lPmph/F+AvT3ZOuIJbsXpOL7Iw9dLG+SlOO5cGdKh6FLz1aaeRru8uRd8uJPUd+9NWbxNF7yHlJF4/tvle8jvYes401/gj59/I6+lIaPcbDmtW/ig6Fh6BGnNunidTyn15ff/iq69LtV1mzZ49xZIE1RhSY0uQ10/GyYP7dz0vQBn23LB0+kD1+mmNBapnp4hY9uDUjuWPCnQ9++rVzFQ0mmiAaYPseBlHDh6ITC7X7RgQEexj1xoJG6pl/rKFPl/PiwuvnoqMiH2fL9Xp6jM9IsBJPjNslKA3Iatx+o1lkHIybi/b/+vdLyirnjOOTfNk1YlQnRX/CmUz30TthpuUZioBfIxAAsQ5jJOLjWKT8VKDqkHrMwK8JLJs3e0zGbZLSkv3GuQNKMaeMsoAKGiF46woztSLGW60RknJWD2qqCL6yw9QPz0p/x0tRybw9xS11IyaEwAtwT8Iso53z+mWb3A5RcgsZKoLgDOpdNSFnj0m8kaLSVxi8geUQXBVywuweLGyP0TDIvzv680vXCWXSkUOk7NC5lZR0aDwvPXWW9zxQ3CX95J09XGxCtM1C+2u77AmbW5fuNnCqo4TyNY+hrzNSfkCd5s2fkUd4RtpN8cpLct4nQ10J7HxotT0O/fjEh+I9T0DdFGFx8NDgrLcVwRY/X56a+8qSuqq3mxZwbHw+fPTbYNHWmSe2XLtC9rfT24s4vy3z84+fXtezBwYQCNAlSijHvO90M9+2b9wOeR0ell/kvjL24QTd9++7DZkmFPp5l/X9HpqaO3Sf7Dl/fUn1rM6nj3Usc6mZMKctBf3SEMk8t8wN/1VUgyFKwF4RfTbqc+8hoxyrdh6ZXOwrcu9QbrCkrT7z1HjJCTXzt08E1Mysa4j+tvZ6NXcgUJRzToPsU+M/YLt2XtAZyNj409fHly5nTizvymN//LBw4clwXp4cUz6s9P30pJ7+PmaPt52MJTHPn2pL/3Lg/V9d2b7TQ9wfhIZuJxofyTI7mPU0E33zEf8GEyuwCIbqTQg4xelPnhOmq7oOOCKz6/uv6JUyH9LyhITbp9ITfcd0qd3xbn9W7a7u0QEsoQJxxb0PFnUfaj/aAbFlm1J9bK7m1KAd+k9zs7YBCd+nJ50DwwQSSVZt8J7bs/sPynA5c3p6fOqaCfCR9DEmiyB8uzIsin39edN8qdWYNia66dFC8RpyI4pfR/986BjWV39Aiw+XNhdDFigKRNVAS4+v2F+SHb3DQGWVyI3+pPMkmeavmpZQl4DtVBVmjcKSFGGfiO9MOkXF+9bDlmcOeaOTmiQoDAhqmH66jJMhFeEbTqjP3KFv1YxhkGuF0Gck5peoedrp+43sRm/44FhBZsEUAIUyqp0pK8sfafF3mEyi3fvXUW49Dt6cYm6Yv3yYVOrLYZwEmOJ2J4lAzrzWJo8AcGu3BLLTk3CSboJixPIXDqno3lLq/HNCuBORpU8o9+/TnkgFHWeXubuiXsVpyaAFs/DSXrrKblCUoXJ1f5QLrbrLWhxkURapqXsDwV4CMhQgh7zy9DPDPcvtIecEpf1h8X52s/OMt+eh5g/FHQZwCl7Qi3AV/YexzE2qV8B1lzYBsVF05ztqbnJGRVSG/bf6l7+v592cJySypLchIInayKeCF3mz7UlYj9gZHClefDx38eYgU/HpyeCoWsWhfeiZOGSrfZeuFbcYxL/7vbncL/lq/Z6M4pMMi3XpOLQKIDCENDytPS3Htu3SLGqD8KnKVL3o745G5p0K1fQ3xar6CuYg48sneEm9cyPnXNIa2TcT8PNq61exK54lJQn6Gjd3LALpYxOH3g0LLgLKq0qPuh4Ug53UN12FDSlY69+Pc4evEh0DxzWl1l3lm7Te4zzuaWPiAN8ho2iAh7D0+TIg3ufeSMI+XEZIssfnPTRaIJch7QfDofO7IrqJUufERGdWNjN/szpOMyAHTtGuaJdvlycef/cp4mzUl98JnseChw9AFlW+UrBnZlL0igogGN7717ordEVoDA4uYJZA5eeDHJApVXfDL51P4c/CTxecua96YRDV6d3qFkbhPu5bDn0iOw+aFZfKpCWPK6JLMo+df4Z6LbmQGBvxhf8/8buiYgrHjZYkyV4s5+++ELzXBw+2oPalLSolizQAa0hux+qz0SnQO4/n5vvzSozTh2zLqUVihHl3tsQh54QMWeBK9Tzy6PO9++/mTCsRQnhwkcN1SLN/3oNw/IPnK740Y0ae3/xw4Qcnqt2gwQluREN0xd9bixDcn+9R1/IPosCF3o0MmJxQU4F0Najq/QnInTxe0rBb6bboyGXvXm2WgCjVTplneJKdx3t+z60+PdQR5YUI0NVmmce/z3XDA9ge61zS3WJA74MGyUBmoDoXA8bcOIhiT8XzowhoJ2yzZtZBm2FAO5uMhwWBZcIgl+/HGsvgz9D0eoCQBJrbz5YS/vEySelUr9gqyc4aroFW4ekEp+bQHiyxvqJsGL+XC4RI+sRnqW44Cd+c9Yp6RZJ0J+DIUiBBKu/NWnfIh4Oxov2WTwilw+aVaJasZoLW9UgLwxDVwt+ll8kAWyNu7QR/izawXEW7VsauA+v4+YVdGeenxUWZCvGPuYTehjJR2XFWckfgUGQNQWSN1xbRwPpvZg8vn/li4/AeJo9DQKQtpElC6RiFF0mCkLJ43kPM6ozAXFZYtyTe4l5QsDL58gNGYWSB6CbGcrdo4hiSAJaumyaXH4szZgMXlUJmjNmBcroDHNjvHL1hgI4pdyWojSGZObVh/rL7ylFAoOMmFJqTzd9PKjCyJPVsTFXjLWN+juQt7xMyywj3M2GaZ2L/xcbC3gwVlaWUgyzOjjoc28uPtrvWnB3Y2xblfwvBcewMbNgogGWQSeigEhjGGW9scz1iIp6Y9MBv4ArrXz3+BlstKiPeQtPGvAyH+UBi6E2DLn90W29dKRnXuVxB5tqsAQMw92BWX5z/8q+m7Z21/ysSMsWyCvSkF33ipgCYDPUXldu7mQjFzpojeOs/PTsHUweWJx8LRZUwWhpWWYe3LKELalFXJgee+V5YoYIVJVwxBizBgmqaUBdhkKtHl2Y3GORR8aYzhqqp2rEcHWViEAlqZ7KMVzqYog35HTb/GZekKD2igibfk3n+V2iCGBKylGArThnPqHEqJW3uXFCx25CwX3tglLxm3SUYRCX2sxEqzUCKOoUAMfCnjbNzFxlul5VzGpaWhaGHkuSWOZ3YDYdVtEfOgbug3XcSoPuZPhZ1SSLKktkPrlHV3ZlGEVXphC72nsYrzl314rCorUZRJSIU93WjgzhW2kHx8leuPvwRhdqnQnU1CGBScQoFqEquBJA1CMpssFo0ciAX8QVV1dyxYDE0lKchJTush4ClawUSVL4cPrCtWeF1r1NFRte660aBSmtR9GFya1PGRdCK/+1agclCl1jfFDro6hCsvJ3IJ5PfJ9rm5yB7xBqRgKAUyOCMlmMNp0EhFUVvPIyCci4d2xxrLJpGlsY4VEUp9k355UP3BXmWbTgdpif85//eMA/AKbHT8EzXGt7TUlm0wGhmgqrtRZJVWkpH2hbM1rob2F+RQUMyHSl/aG1dImAW143WmpsCaTus7buKVs0Z3lQzvxtJ/0syU3VT9MWKNGUnUhQUSk/yVCae43rbRm4uoIjAnlnju+/qrQgWwtdIqpFCeHm1CIpvLh1wYT7IldXUyGoMf3GCTY8NNMgg5bzti3zChfv8ptZtG/b8iDLeiOWl0sqgVUblFnunueZLsz6U5Jsna39O9wTVHe0ayA5gQm3uhuSmvavxh2jfswUphWKnXsImhuBtloAQJIQm5WA1KHcksB69YrAisfSulfpNTu7Yy98eXhj1df+EEjwD6c7rz2Lsu7Na9iVSaktrD21XFiZWAwDCINplVEhtCPt4DghAomgwZKUjQ2Pl2cg4Umkij1uYpEYYMk4CKc4KSxXTBHRQNbYeSniScsuR2w+hZsUfzjQMT/KaerltklUY0ZSmaYd498IpXMvGygy4dGr9zyTUZ3qDb+mGFKRQAIwRCIOhwHo7iH7H/ZtsL/BZfjqeHrEgPAdAafsXs3sgOwhb0httUlbHs6glCYkKpdru1kLRmEJ8s5GJKy1P74E4Em4phwiRLIKWX2AFbFw1M6f19kd29ShzfstNGaHxijNnS9SnPzabbZgoigcDg3QzhH7do1uYEHNS9iMWqSFMRFT7+KWR0atMs9fEZi4V3ORVQ+PzNUoAyXgYiRj1k+rZq842flokHutCGgKHS/8xBOqBERLSVoqVSnFxsyyvUPIPvAi2zzDdPJdw1YoVAPkjuXGMqNXj7WLiNwxds228LYI0ILnoXM726LOx1Bf50qtFvGab7gQAVbtD8suW20+JZ0UnxzoSIxyYjToylrydy0WFuaU8wGJQW23rSoIreTP1TikbWjBAvHP8wVTdUjVBR8LgN5UfRKV0sEQ3IvJ4oXoUwQVBWXq8YQFcRl8dncPOxKQioXitmaLJtDxQCaslE8udKW8ciFQd88aQKHlfapMCjdc9kBhsCgggyW1VgvpOfaw5V0497DaYrAzG103wa4urRADFsR5n1kOdK3NaMauDPhGchanr2vDezBY0z5BG2/cHZn0oVzaAZlzNgRNohBQQFjKhwFNyuXUzYs0AFGNbQzAnbvvqkIMGDVaRKEx8tqD4Qa9C6Rl6EQHt97m8wbrkAUFr0qB0WD95ro9LHtk0Iwf7q188JEj7UCAAMzj8NFaZHzragoiaciOrIWz0wZ30guqh7IoYk5+tbJULZgopG1kxYaf/u8zbzStobyNJIQFFXxIm1wzGtCgljqEmakZXEZ3b1PFQ658SdMJ1h9WhxlrlgHH7rN5xo3TK5NeckCd48QZWzBRL3IKRU3ebOMTUl6jGX7lpmQgE6E13sNEYWRyVwJLmvMnGP0qFzb22X3taot86/rHSxroof0FwIjse4oqbtPTKwX+HVX6I1jA4UIUajMzUKggTovPLvWQuz0pSnNXhpIpTRel7hibKGw9oi/ZHC0jUz3EcX5v/mSNk228hzJunDv7YJaB1e0LSWLrKf4GWC3pwPEG0dsiDx2VOr079XsFULM7LN2Kjip4k/iqlFF6O+YzkHVujeerh2hpowOu3j2X7uWTcfkWF+BEkpbjQwQWEy9Ljb2d0WmYKZNSqxmIRGeSQOq1hIy+PU3ZJAxG122o3t41uYY/e6h0EVm/7Yjzmo/+bUsq5D7bw4iiE9iXfTh67zqvNcscwIfPQit7c3xB0jOJhYPsxa0ssY6bQZMrgf9hyAbyfv+30/fTfD0z9iRw5d1VU2MmLetBE4x+27Jnxz7a1B+0JURDK2MCQx8P4uMS3nTqafe1jyHaTOjGPPLgzDl/A9dnFx7A1qt7GOAabbCoRfDxRbrY3Fz6IiFNTO1nQIQkebuCx84HczMiR1i0srJImrIjMUa7k08+OnlsqK7bq7PX5daoWNJswUTJ1oPGsK/v23PCd82EriA3XWjUxRyb2VBCad4vncftAXPOx48wgDSrxaJuvxVWz5AGlb6+m1HCrrx1uRDI7OTuu1GRUZ9eJKumr60ug37l43SJo7nsYXyWkOpmUb+HFsO276Rf/OINR+rC1KwsvNhQT1b6O/1jgbjqOLMQADu1JgmRREwSKvUaPaNvqSm7ifVbLb6bq+zydaLevCpmTQhJ3i9dGuqh/QWQmvTlYvYwc03yHPRrT0kyfgmy2gt2nYuaa9B0rlK6lRhVQE18hWOUspVdmdpoEJIy9GEQz0x4U9HTTkxSLbZ6YRsgLkn4wLceYfEPenD+38KfPVQhOW8Kn/IhbKtzAIAM+h/aGGCv8DZ2K9bM+bj22KwNLwcP6mGUnkRANzR4DHts0IjDi491G37Stp+PC/pupaBtjrPT8Em+DyOWzx692cZnjDn6okDcimVbrW4jBtnGRf84JeVl5OkI+9qxNNVpZKBx3L6NgXEfD6SH2JPwLC9rMhB4DlLd0KBrnLJ9kl0lMOz50+UhJvIidp22JapyxfylY7bIrxoNjzkcTH8c5XMoVSBPsMPI0zNcm9y6+R9Gy2b4z10fBEfNNj9rE9jPHPOIL2yq2gh2qzYuL10VMXf+Y4C1XX9wb5i50zwf4+tXNjinfIg/MbYuHKnHzPDVuctmTBkOUAbjFm+aY4YDGtMU5l+KWrw0VSSXovOIFRtcyKA6+W4WcAv2MmlDG9GUHcB5z1428+PKeUFjte0D5rmk7+EL4RZNlOS4bnNoyco9vmPPyY+sh+1JCqY0krAqLjEV2Gz1UplvNFbL7sm1FzBm/YLnXlsUPnv4euN+ky3Rp7gCaaMi21Wd/KmhBtCNZYgdmvJz6MGniiB283+e3kvlHp2WSdcexNuX0rkTumt+NwBG0H9z3jUfs9kGJsZjCy0xrGqe2sSOWjUykBe3r0NgXO6B9E/2mtcGJJY/8MB1kk0/fq3frvqkpof2F0DLpdwEMHM61b+7h/fmeRbKJti3hVf5scdmjjjseKxbl5O2RT4usruVkFpXJnGa98X4uuEGZ+0P8c/neKragVphVYFLXl4t1B/izESebfvufJvjpHVZW/m40Tm0iV+UzK/+kOEy+dHV0YVlIhqT+nXJi2w98tLJkfIfnORNVheJOkQIoFlBh2OCaq9DTLc5ybcmFvCJ+jQ8tDK05uzUgzFTa37hzFecjllR85vktP9yzP6GQuBN/K9Fe3+pADpM+Qhu2cFG0SGDOUdi5tT8HnxINrg2FsNtQdrdKYV8nB6t/u4RpO229+S91eV8Ak25YiXIefiWZ9rH21nVkvW8L+0Ol3Ex8oi1RSSaTf35VGBoVWE1xKQql5DGR3KHVxSLSXrazS0o/Weg+Ky93bgLwZkEbboyobRCRlXM+I8uUp4k+z577FtzHdIPSH4cUPObZPJD1LEB+zgcMbFmQxm+34JTvCllHBxdl4j2/FrX2i4rd137qaxMQGYya1c0dTRawpL9d0IqKoQkOkMZrDr7+SuUyyovVn0TUY3YlAWqZydvZDo9Dpy4s6FCpM2QSzpvbc1ZTSZKVbFGLTPfUycHRVWVVUJUHTIWaiwhP+75R8g5cAirQRturBbLrwm67ThyO6yUT2HKbXTVIU1FbnSoSQaXuNvDiyvE2nTtxsvXFKeQPsRBV5OKvProgS6/xsWo1Ti136ejVTmlHAlTVwad/aA8VxAlK6gPAUnc9j6/txrHJ4jqV4dp5WsrGyRmEJIcE1J/yH+rrge41QJI/J/H+DcvgBK0eX6ULF/lBP/z/Y+oHpO7mapkqyaqIklmxZzk2IkFGKK+GA+9renKtIOSv/Z1isN+Gad4n8s4Urpu41Fdo8KqZiHJ/P1qqsmQUybIkyjfn++zOI4msnQ1vsNf8D7pdRHetDNbw0YMCE8z/JaXsaFJ7Ga3jWsEwlP11TOF8Eym8qyUE39u+84S+21+1o12/KMwZFbjN50ACKetr2LVaCKNjXzKoAXQco/T6sAQnkJVqS6IQNXRtKUHrcXQbcUnMtBaNGZdMOGHp89Br7kj2H9gNK8pOwjHYKh1cC2bKITX1lGZ0qhIKMy9kQQC5vY21SBgI7XUn9bVbXRatcjqh5pkQBN1mRqNmNRl7ETXGcciM71WWTbVbiGCWLelPVd4pqgtzb45PfyJAghyn94HvXb1bpV9QDKaYQs7NSCCRKPpNg3n1ebzpX4LfayRZ9v+Av6Su8rSkovrVh4Q6RvAWdfjCt1//NlbzeX8LRGmXljS+3iWx8yDU5EnMf/loPV7L3/Atm3p7aZ/HWjmyLCdZrZ/o9tbGMOhvx1wKaR83/WUv0gPGGafEzvY7n+d+qVYkwVbDxibIR91+kv4a7ZjERx69fB4/rkU47Vh89rJXQz+IQ9mYPUsnANnz94wwrJeYJSWh9+UNZDlN350EOFvBoZlbc/6q4VoDgzD1f4bPyjT7mDoxpbfe6jxF+kBw7D2/EvVDxF07S3+SgH+2/wljhMiO/Qau7nXX5H1NwHpegZFejY6R3bznez218iDgICAgPD9QR4AQkBAQEBAaAOI40RAQEBAQGgDiONEQEBAQEBoA4jjREBAQEBAaAOI40RAQEBAQGgDiONEQEBAQEBoA4jjREBAQEBAaAOI40RAQEBAQGgDiONEQEBAQEBoA4jjREBAQEBAaAOI40RAQEBAQGgDiONEQEBAQEBoA9/mOKWCsuwysbYui/EHv7LFe3370g3gNWegJbnlwP82uBm39jwFvsN9nL716zCSghfXjn9ij/fravLP+9yZlFeanVZBsDZlU/+cYVyr9dwOapSUJh26lWk2wG8Q6zvVhJT7/kR0Arr7iEnm3+Fbr9LK97f3PYP8AgY6tC23tkeEK+Nu3Pzk6D/BgghD5dmECqmYbSYm/oHvo6qKwcMWfoG0jIRaQlxhMYpiJKTUfCVViqrMwVfjRGx9qcbvdPGLCIXFQNtMwPiW7yDB6JLPWJguZNFrv+EuKsWXVMnopiJUMb5MCOuaSLBSqCwbJ9YWsqgVb47cKvDy83ZEPuL7t+PbuqqqlztclnwIiTqx3voPfXJaykuMPhwGmJO9Lcl/p8/KwaVPQsJ/wU9YE+H5533uTlr1NjrsMIrt84MT6RszkeTGnw2769Ft0D/McQq/PPl5zcZtqVz5b1qfrZnhnu32YVa45Led4TtxEy/O9hC3Vs/toEZRUfyWw3cHOA36bo5TVp22L+owjuX7XRynrDL98vLDWJPBbXWcbY7ISTky5lDxthOjKunhZk4PK5QnMfzua94vDq2k/1H3Wf3YKnAQeXjy83El5tMHMLref/ZzP1hxoZy5toN95ozk07s4avKhE8Z4Lr5Q01XKDPyzlhzM6ajXOFCr4FIiPZwTBr++eLJCOYjDxE3wWJlSEPk2izPbLfRl/pGULGsBdYeL04eQpBPrRVTuw8UTRFYJkyz+UPeK8Ofxn1mqFRQ83Rf9sevkiV5NTTuEBTejo186Tg5zJMlEnC9Fxbhqsey7ytikPH9B9D8fuDx25qzlJ9B99+yaPtJQXCxjabdj6jJxeVlxLpYrkgFUOyb759OyobYBYdbT6H0fHVZOdPobffC6NUjLb525A/fZNpiJFgNYCvRDk48sE6fssF0RZr/L7vkKf3GLrlOYRY/eR3ZYmaOx7CSHcgsM6208XtyPJx/iCD5qZwlg2/58jV5dJgHAPOdAcrZ2nNHGEeY/z+OdOl3KaEkCDQJQeB6OsnuJlCJRhZl8pssjvkmFiO7lJlogVUMCWKMJ45zDd/0aPyK019+0Ef9n+a84Trgw/siii8QL4yc2GaI8fkXkBfKq8WFyregPir4w6HvK17w83z/6n48w9cr+E2U2m4+HhSj6ENDOX43G6E9ef2Gy4pc0v31T/nNp2VDbklj5zSP7I4jhS9sjse+JtPx5ZDJp+E4rLQCUc00URoqlCbqEfvI92vH6UQrPv6zFkUD5TbP9EXD40hyNVyEG180SnHykxV3OowNQ+Uq7CMWb6CxpMjlIhsXDRj45wdPYs6LYaVWl3Vv6ZLcGASCx3DeDdbSMihwzPQCXaKXkykyXVzflFSG9jr69+ZsOpM3q5f4fvJf1d6adHCdc/Ch461O3kR3fXY6+W0IfMDpkmeGzsMM3YqtYo2YuWuHBxEi+nNu+7aalX9esS4dTRXYDgvaOcW78BXVexpGDByKTy3U7BkQE+9hhi3+J2HLDdlSf7Ev7Ekv03MdETDC8c+jQ0RSOSZ+ZByd5sJXCczOuLzl45X/ltD4BIVsGmuGVknQa6fruUvTtQlLfsT9t9TYourt1wvkMIINWLJkV5TD1YpBRzKnIiNj3+VKdrj7TIwKcqEV3Z6w7/0Ye4kho9xsO4Qs9f9t+ATVm1e7OVCDlvry+f/HV16XaLrNmz55iSYJgpWA2o3pn/7rvWSGl07jIYG9bQqPCSLIfbJ+ZYLvEq3TvlYLxq8KG4TMblE41vLjwarPyrAmf25fCe3PjwJIryUW0TnNmB/9oRlB0skmnZh9+mEnzHENvMDeWFDSIvsgfOni5etKSn8ayMZLCB0FbHphMW/Zj3v6geMsgh8w911MFpt6b5o/prg2p65MEpJyM28v2/3r3C8qq54xj0zxZ33aXqRZR3pUHORinpeONcQ3Oq2lb9gdNq/L27vAI1Jhz8zwaGVnr1VgrESf98PGzZ5OzJVYjjy3ytRJ9OBy5/+DrKqaLf8SswTXLv3BZ0vodhy4W0Ab2o0uby0s9dd6bOwcX/ZqYhTIcNj10emXUj80aKlOhfGl5+rXVZ+//Lwd2Hblsv3u9oE+ObwzP89gdOswBrzCC09vWbvsEpFDU4NnXu0xdubD8YL1Bhk1DXz+glnLjwtpIMjQZrbQk8ZDfr7/n6/XasHDyAAZaVPT7+v0Xrn4oleo4TJ4eMteRWpOYipxLlteL+Wr1xmMfPeYdGWYqbsK0qrPiX6Fs5ps0nv/hxWw6EJajYYAqvGoSGcF8nw90uhZOj8hzYspbnO72mQzbJaWlew0+GYnKr2oBKYga7HK9y+fVOysaO1q80MVLJLlDzeUW08no7P8RgUWBfcujNynNVAL4GIHkjwkgY/WoooroLz9A/fSk/He0HJnA31OEBk3dQyBb+xjyNiflC9xtNFkPwl9Fe804JWWJCbdPv/0w1Ldnt9IzO9fOuW5o1Kt/V5f7p9ZsoPc5E9obJ85Lf3b6XlpyDz9f08fbDoby2Kcv9VZJAS4+v2F+SHb3DQGWVyI3+pPMkqdRv7xNOHH37ctuQ4Y5lW7+dU2vp4bWLv0HW95ff2I9q+PZQx1JcPGDSQt2vus2Y47lk9CNYWTTo+tpCklOpKb7DunTu+Lc/i3b3V22+pt1HmKfGPsF27P3gM5GLAIKSFGGfiO9MOkXF+9bDlmcibI1+8HL7m5KAd6l9zg7YxNUcULSc1R/sVTeGG6F99ye2X9SgMub09PnVdFOhI+giRWC3U595jVklGvF1iubg21d7g1q7FBEJel37sclPhDrewbookobl26mbX3QFuXBwXkP1vfdme03PcD5SWTgcqL9kSCX4uiA0KOpDn5zDD5sv1QEVAbAKHKD6NZ6GVkvrpx4O3Msm8b5cP/Ci5ItNLzwVdrte3fjP/QI8jK9fP7AYAHr7dp+emWN9bnJ9OOKsE1n9Eeu8NcqxjDI7eI15fCzY/KBaU8rZoMEJVlq2h72R00rLz3pHhggkqqm3zY1KuClhS8MWVvkHOTfl0U20UEVHA8PCcpyXxFg9fvprb2rKKmrerOlOftWLF6V5RA83ODlhUs5tUloyMtDrfPjpkUN3XTPfMSPweQKLIPIoLdgqMfcKZy0YwPmnMhx8gvuS6cbU+tupcp4mZdmn042CZ1ni681AofO3TwTUzKxriP629no4UQfVAwShypRS1mtsGpNcqaNMun0tef0Z3Sx/HjhxDCBYfrmgfpAhjLqMd8L/eyX/QuXQ06nl/WngIZyamMza8QUpFzaseEl68g8YwIvbalm0xLnpKZX6PnaNfab0jKt19lAd5IAD2RCKTD0y/PCUC4utlwOVZ85VkEU4dLv6MUl6or1y30HldsXUlMypa4jiuxsBDigDmw6oBp9TPtdEXDC4tOSseTOFfotOicpNuN3PDCsYJNk4A8JQLArt8SyU5Nwkm7C4gQyl87paN7MDSE0zdmempucUSG1Yf+ddoH852knx4nC4OQp6Q9eenSGrdSz5Nrca9SR+w8MM6i0fH91ZfKDPGFvCzRBHoL2w+HQmV1RvWTpMyKiEwt71s8GRLn3NsShJ0TMWeAK9fzyqPP9+28mjlFsoWMOPrJ0hpvUMz92ziGtkXE/DTevtnoRu+JRUp6go1nWvVPX0N7354zqBblkPZxx7sGnn0crJGENXHoyyAGVVn0z+Nb9HFGge+8xzueWPiIO8Bk2iqrIzj9wuuJfN2rs/cUPE3KE7vYj+rlsOfSI7D5oVl+qtOR6nVjZp84/A93WHAjszfiC/9/YPRFxxcMGYxWC0QceDQvugkqrig86npTDHcSiNlQJFoeRwZXmwcd/H2OG+nx2VqPS/WhrXF8LrOblAeLPW07HYQbs2DHKFe3y5eLM++c+jcPHX46F3E+vWjCeXmaTOXpiZn3eaIpNg+gCho/ekXPPP3N7Ez6lfhIYeHdjorEKPdEnLV6y0REVIHvrcfHK3fLunmr6DPNPffSF7LMocKFHey4Wwbzychho61IabKHRpG2/Lt9qWvWIc8+0RY1yMbMfRW56zw47uHF9B0UvLvx0fGsiGLpmUXgvShYu2WrvhWvFPSZV392XAg34edXeAYwvxpkW6zObyGuyh32jnlnyJfXFZ7LnocDRA2q124Kh8joyfzlwOok9IXHjDHelX4ELlfGkxef3n8t0Do7ux6pt02hKx179epw9eJHoHjisLxPAn1UMUuFbG6XsblvSsLCiz2cbN8kfbfQVcXQn/CQ3G2gM9p3rqat3SwdM1esRPk1xwY/65mxo0q1cQX+byoZywtlKrchHuovOF/QIWj+GhZHkNmVa4oKcCqCtR6/vnSSV+NwEwpM11k+EFfPncuUpEv0/K+UvocbqLX7IyOFV2GKlGBmq0jzz+O+58gJ+ERgcvAi7BxbIy64RSsdyY2D6IgUzgkJ6lSW1XMZr7kaiCF38nlLwm+n2aMhlb56tFsD+IQEgOtfDBpx4SOLPhTNjCGinbPNmF50xDF0t+Fl+kQSwNXl/hL+I9ppxolAoAPRMdeSmJ6ToUgDBiEWRp42n6VHBx1KBfNgPYeQhdGyUW/+M+juQt7xMyxTW926Vn569g8kDi5OvxYIqGC0ty8wTKROlmxnKexsRxZAEtHTZNHmiWJoxGbyqEsCg+k1itoTsmZccew1USzCyL5nFAmUklrkeUbGswqYDfgFXqklicWF67JXniRkiUFXCEctF1VguXuajPGAx1IYBAQzd1ktHeuZVHnewqSIPhrkxXrl0Ix9cl3JhKe/9q+T0amVeKJK1i7Nyn7D5hB5G8lDFGkoHjBvk1Kw81Z/uZsO0zsX/i40FPBgrK0sprkh7VQCM/DypEIDINlZ00KDHbwjBzLcjdefrNzlCg9evSnRc3CxwoBQtLwOzk76iPqzd7GnnXiYUlJHU9Clh2HZhco9FHhljOmuoXrvtFJXJJDBQW6DSqO2u32pa36DG6qSYdLHR2FF1G1arspI/AoMga4pcQJato4H0Xkwe36/i1SdgNNOOJk+CZmzFqklCQ14ieU00FAjD6uCgz725+Gi/a8HdjTVrt6FhVJdcSoetx/Rt9IgCN+3kijdmqw4Nsmy6ilAqBqkhZbXCamqSoMZxuinNxsLVUedEYuIX4VQ9EhCXJcY9uZeYJwS8fI4EVL/TJCc/4VRUrNnkxEGGCi/QpGnB1VUiApWkcqpon2PgPljHrTToToaflaxOfnLsFXpiBgpU4RRNRrkLzHxCiVHr9qBijaqc9NHP4/GVetTPYoGfu7i5OV2O4VIXQ7whp9vmN/OCBNg/LABO6NhNKLivXVAqfpOOMgziUpudSaK1GUSUiFMNt6pICN+Ldt0chIKUNoBS/EE1exmhmlOyWqOC0MpDjDadBIRVnHprgKsrOCKQd+b4/quKgChbC10iCpSrJIpSJFqXivKfDOYXyZto3t3wyN8VYVDGTrp4FOAos0XVCISqzb0hksKLWxdMuC9ydTUVarpeLxa/ogIGZDpJoSe0li4RcMu5tVKjasoCavOAv1zatyrsg0hxgDVfsX+/cghOYBIxTZWu9fLA/PIyCci4d2xxrDK+sYURVlgib0xEhjamTjvNQXLp4UB+mPiiuMP/8vAeY83lI/yyGk0qy4DVYlCAsJTL06BPkvO2LfMKF+/ym1m0b9vyIMtvfXSmBgyBqo0C+cXy7kb/6xJdM9r+BtOqp81qhKvzS0VA24hd2xHC3AquBBD1lAJitGhkwC/iiqsrqyWAxNaqaUu1SWjIC6+hjihOs2/OKx+4K8yzaMHtMD/nRnMeNcOAq0sKRIBpxGjkgd/89gSgnbRwLVZOjUFqMjm1wjZttLW1gSbR5WZTzpdKCh9OX7j2rNC6t6liI7oyMY1yfop8ArBOREKNmE2bllyJUgms0g7YC18e3lhFVZl0FV60WTBBT+RaYSpsoFcCE25tp0bmuztLbz4hF5hSynQrnU2a3UNvlrvneaYLsz7MHxVAatq/GneM+jFTmFYodu4haH4wKhOLYfnIEPPP2hr+7+d776qVKQ1PKhJIAKau/ShA4XBogHaO2Ldr9NdH+aQlR5pPDIUloAHGOSR2Zz/d+kjXm4uiDFIYEzH1Lm55ZNQq8/wVgYl7m81BbtcioUQxr5GJ+RKAJzXROWEtlkXdX1Z/DGen1yTRROnqd3u2LI9i2Regu4fsf9i3Lr60+MgJ+ZCXL1RI1ozrr4Vu16sjKvJW8qtkockCm/qVsdr6EPPFAEPG4dT1qcAq4GIkY9ZPq2avONn5aJB7u+xSIBm56YD4lIwyqY1BnULboG0NNGVa9bRZjSgsSe7V5eN9SU1LQeHx8n8SXq2AIjHAknEQDq8IxBVLVafQGvLSCERyGb46nh4xIHxHwCm7VzOtVa5pMIwaFQk4AknDtmvqO8PjyaH151LG/eRKbZxHo0JpTlm9sJqMFs6u+a/UlLyKRACrjau8HLH5FG5S/OFAx/wop6mXQZNysqbP6BB96OTWlP6RrnIjhCiaTQtNoeOFn3hCFTURYIKK15QW6kRMZeGWJ0etqs5f4d5cE24OsfUPPLCd+vJ3PN4l16z5WxFoKUmr3j6+RQByx3JjmdGrx9pFRO4YO43LYfXAnHI+IDH+pHeDIPxRvnN9VJdWiAEL4rzPLAe61iY4kFF7AdI2smLDT//3mTea1upHliCSjRVD8vRlOq+fbguRUBgsSj4rVPR4QJiZmsFldPc2JQFl71wbAo2R95ww3MCQIZKhEx3cepvPG6xDFhS8KgVGg/Xb/khV86VrWR6IZOzKgG8kZ3H6utbeEYG0zE21wbP0T4KhxiRxeUl1nefQXByI5jTMhLf9wYMqfd/uiifQamZk1QVcMWBA5bmZRUDPVZ/WlD5x7D6bZ9w4vTLpJQe0j+MkmA3rwtx5/dLpz31DzWvnOE1ou7RVCTZpWvW0WY2Qlo0tE9xJTKoabsGAFPVoaMEC8c/zBVN1SNUFHwuA3lR9kjbelAmePcsXzNAjiTglVcokNORVAyyo4EPaZNUBAda0T9DGG3dHJn0ol9o0b6iQlrEbE5xMfFc63IClkoSBy4AVOndcTh85N25HkH5dq0ah5dnIpLDa9FuTyakXVpPRKpXDza6Smw26MjejEOh1opXFZfDZ3T3sSPIRmFAMmpFTp2f/yYZ3AjccuR+6w99cKaYm08IZWzBRL3IKRU3d2BNmUjO4ou7ePBJAifmaZ2NoeVQZSr3sqjC7VDKKGc8TMAazuCp+U0MdtaMAGP0qFzb22X3taot865aeaRF9yeZoGZnqIY7z78V3ro+s33bEec1H/7YlFXKf7WGkkjvZetAY9vV9e074rpnQFeSmC426mLaYHKmjTz+z65cXnOz6y3hHkPuZb2RvpzkkRKIzSSD1WkJG355GeoY0qPT13YwSduWty4VAZqfoDiACQx8P4uMS3nTqWb/hlWQzoRvzyIMz5/wNXJ9deABbr+5hgANVbS23htKZf311F7ZFeeyY1oF92Yej967zWrPMAXz4LLSyN3ft406/83D9zSFGtq82x3EBVqz6EFrD6CQMRrdvN70FJ3KtJnqY1S8OZR24GDdkJPrA2VTINsRbl2Kopk8HbMHDdImjuexhfJaQ6mbRbm+nIXUZO7nf3e1LFqwUzBnjwxIVQdY/2GvUdkqr0mvatFTybKsaiR19vK1/Ozd/Z7TulM4MCc7Kxnso48a5sw9mGVjdvpAktp7ib4ClMPoOIN+5cOrmDF3bmLNx5QArgjXnRfnyS5dxe8Cc8/EjaqfZvNykZxILB9mLW1liHTcDMgRJmzdUonWgt1Hkud0h0bQ1nbVFeEPHWlFxDkMmDjy/bt351PELXOqGBQQWEy9Ljb2d0WmYqerEV6PJqRVWg9ESYcXE+vOBczFDxxOPnX2DcpjnbcCE6aiCN4mvShmlt2M+A1ln+cChsZzsWg+BM5s+sfPWdSe3pXrvsy1rwrQwbPtO+sUv3nCkLkyNzgurx6dBuNd3ySVszK3LBCDjqC+6EFgivIwSe5vUaRiP2cQGHKJthRXW8OkHwYguolqLkeQ1rqN2F0CL7+Yqu3ydqDevitlCBywuSfjAtx5h8Q97f8W/n+/sOHWNU7ZPsqsEhj1/ujxEPisoqb9Ecly3ObRk5R7fsefkR9bD9iTNNWwxPbLjtBuhFSP2LLVURDIK2R21q4lIVKeRgcZx+zYGxn08kDoxeO61ReGzh6837jfZEn2Kq9hhArSc5vkYX7+ywTnlQ9xO869i9ZgZvjp32YwpwwHKYNziTXPMcKCF1RVNqJduvlPdNYxZvxbkiT81p+u0LVGVK+YvHbNFUdDhMYfn9/AIOTrk46g9QVYk+7kjXJ5d5gtUB7cNo3sS8KaONjQg8OlipDJj1LPN3GY/qVI+Eziwboit3KGq6XMr5fHPoQefiuQJ2s3/eXqv9ttaizP0vbC1eubOc2vWzFsFgLH31tf2nhq0XdJyUgqaMa16SG1VI8ku8FpY1cgdu/o8Bnjb6Yl7xm0Kn/IhbKtzAIAM+h/aGGAvn1bgPLYvHfpy1W7PcaQuASN7pV/iKjwnRT0vh0+JqcBmq9fX+YPw0+Mon0OpArl9dhh5eoZilVXagqESPCZvOlm5cvbueb8CrPu0Q//zrk0LrdN9+UCdHtejzo3ZMaN20qnVbcQg27joH6ekvIw8Mb++WJpNTq2wE9WM1l4oFOOMhk6o2Os0sRTo9o5a52uJx44NGnF48bFuw0/a9vNxQd+tFMidSCM5D5ypfS8U2qDbpMk6IYeP3J8zh9OUaWmZdO1BvH0pnTuhu8bXSWHMioLnsheFuw5fz+s3mYs+hRaoNUqtbnmDbJ2if3RPeZl8OoKjeZ2EWt25A3j6jutmWxe/qnEdaeTbBJBY/sAD10k2/TS/qKgeuOTl1UL9Ic7M9noKDKGd+DbHSeuytvJxzU/fZ499a37hzSe/fTy55jfZ6ae8xz8pfsGKPTtAz/vS7nAZF6NHq7kJpTP1YMzUutS0zHxPnRwUVVVWCVF1yFh5gPqrOPMVp2NW1PwmOe2/HLO/NhLRfvCKNJ8lZeXVaG0qVRGpXhJIPyD5cUDtb223vSfvrS7nE2g0LTTYceR2WCmfwpTLsepQXYh+C07xppRxcHRdIvprIkDbZeWuaz+VlQnITGbN4g2kIjZkMOdIzBwNukGb+EXJ/OqP1UtHGXxINrjmolsL8igandnUn08FhlYVVkNMas0qko7/opOcGRUC5S2QXdMa5t84uuD9i3QOq894S9W2qjt+7Z7zMi6WTqvbmKGuz/Fxt4cXV4i16dr4dn6SDM10GffrsXEwv7ISRWYQlJ2DurZ1vtm06vUsL18b1QgItj8seT1gQQVHQqYqNwW5TH50dXRhmYjGpNYpBGPQY1Hq7RnFIhKLjAFzpzWRFz/u+UfIOXAI62urwzuOj+QOrygWk/S0axcGWzZUgsnEJcfHL+CUS4hMhUSWzx/711zpvuCybIGq8BDDbUHa3SmFfJwejYi2rzdIiKrJ5NQLq2a0duNPCcfLLywIK+dA1FqzYbrNSb41sYBP1KfhoZWhdYk1kvNr7s57L8XU3BRs0rQoTiF9iIOuJhV59dErX1sZ06hSACRx2/HidhiOTxHRCKBWfkZBlKxApewVC9J+n1KIwemJvzotik/6bdWpIVoQ8DwmQOUE/23jOpIbWJdf4xpL8EcFqMEgJDkmRPWEShaE+vJKMn+/mmoy5JQJ8iTK343vvnSOwpBZze2WgPDaOm1+gTKEYzBbYVsQnsnEf/2tq6u+aRwiUHU0DU3RWgzdb/kqQr0ETZWudfJAOG39BgWVJ8hoeu/71+jSitSzwb+UdJnl37HRGBeFoTLU6qORPtFEXeaf+AJxNJHa8B1Sf1DbLZlWPW1UoyICjdpAISzdxgqRp8nSZIP1eQlzbySBgLm9TRtOH9BEGrtRYi0bqjxZSmtMXpkAVV9j2ZpIuXFhNRstmkxvoGsITzPUnFizcjZpWqQuYye6zjgWmem1yrKpmsHrilp48ASSUfXFzQdpSBN19P0EUIXzavP5Ur+FPtb/qC83/DdA7jn/BxBknveddzy1Q1DCYGNk7PqXgWaODNtpZovcrmoVGMOhvx1wKaR83/fl/J3qSIo1WbD1gLHZn/eBJoQ/zHdznCgtD78payDL9pi3IbQNHN2yu0/IthkjnOtnryhqB7/VU9Au/4I3YP5TTAvDcLVv/HpmhKbB0I0tW9p02u55/o3qCCLo2lv81UIgaOa7OU6I7OY72e175YagCkTz3PSTZ6NzVNshK201h/+HgZgWAgLCd6VJx/niePL3lAPhX4OYL8YSkbsyCAgI/zA6Te7YypBNOk7z3mbtIwvCfwxYDKOxyPZ5BASEfy1NOk662fe+vYCAgICAgPD3B9lVi4CAgICA0AYQx4mAgICAgNAGEMeJgICAgIDQBhDHiYCAgICA0AYQx4mAgICAgNAGEMeJgICAgIDQBhDHiYCAgICA0AYQx4mAgICAgNAGEMeJgICAgIDQBhDHiYCAgICA0AYQx4mAgICAgNAG/g8p55HKBiVJuwAAAABJRU5ErkJggg==" alt="" name="Image2" width="616" height="378" align="left" border="0" />
五、枚举类
From: 使用枚举类
使用默认值
from enum import Enum
# 定义
Month = Enum('Month', ('Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'))
# 遍历
for name, member in Month.__members__.items():
print(name, '=>', member, ',', member.value)
自定义值
@unique装饰器可以帮助我们检查保证没有重复值,这里使用了“类”。
from enum import Enum, unique @unique
class Weekday(Enum):
Sun = 0 # Sun的value被设定为0
Mon = 1
Tue = 2
Wed = 3
Thu = 4
Fri = 5
Sat = 6
六、举些栗子
# coding: utf-8
# <h1 align="center">Built-ins</h1>
# ## Types and classes
# In[1]:
type(True), type(1), type (1.), type(''), type([]), type(()), type({}), type({1})
# In[2]:
x = 1.
type(x)
# In[3]:
type(bool), type(int), type(float), type(str), type(list), type(type)
# In[4]:
isinstance(1, int), isinstance(1, float), isinstance({2}, set), isinstance({}, set)
# In[5]:
issubclass(bool, int), issubclass(int, float)
# ## Literal representations
# In[6]:
bool(True), bool(-17.8), bool(''), bool([]), bool({}), bool(None), bool('')
# In[7]:
int(''), int('', 2), int('', 8), int('', 12), int('', 16), int('h', 22)
# In[8]:
int(True), int(17), int(-17), int(0b10001), int(0o21), int(0x11), int(17.8)
# In[9]:
bin(True), bin(17), bin(-17), bin(0b10001), bin(0o21), bin(0x11)
# In[10]:
oct(True), oct(17), oct(-17), oct(0b10001), oct(0o21), oct(0x11)
# In[11]:
hex(True), hex(17), hex(-17), hex(0b10001), hex(0o21), hex(0x11)
# In[12]:
float(False), float(17), float(17.), float(17e-1), float(0.17E2), float('170E-1')
# In[13]:
print(complex(0), complex(1.5), complex(4.5, -7.5))
print(complex(0).conjugate(), complex(1.5).conjugate(), complex(4.5, -7.5).conjugate())
print(complex(0).real, complex(1.5).real, complex(4.5, -7.5).real)
print(complex(0).imag, complex(1.5).imag, complex(4.5, -7.5).imag)
# ## Operations on numbers
# In[14]:
abs(-3.8), abs(-2), abs(3.8)
# In[15]:
print(round(-3.6), round(-3.5), round(-3.4), round(3.4), round(3.5), round(3.6))
print(round(-3.1235, 3), round(-3.123456, 4), round(3.123456, 4), round(3.1235, 3))
# In[16]:
divmod(13, 5), divmod(-13., 5), divmod(13., -5.), divmod(-13, -5.), divmod(3.5, 2)
# In[17]:
print(pow(2, 3), pow(-2., -1), pow(4, -0.5), pow(-1, 0.5), pow(-3.8, 0), pow(1j, 1j))
print(pow(-2, 3, 3), pow(-2, 3, 5), pow(2, 3, 3), pow(2, 3, 5))
# ## Strings
# In[18]:
print(ord('c'), ord('\xf7'), ord('•'), ord('\u2603'))
print(chr(99), chr(247), chr(8226), chr(9731))
# In[19]:
ascii('Ça me tient ∞ment à cœur\t')
# In[20]:
repr('A string'), str('A string')
# In[21]:
a = 2; b = 4.5
eval('(a + 3.5) * (b + 5.)')
# In[22]:
message = input('Input your message: ')
print('Your message is:', message)
# ## Creating and processing iteratables
# In[23]:
print(tuple(range(4)), tuple(range(4, 8)), tuple(range(4, 16, 3)))
print(tuple(range(-8)), tuple(range(-8, -4)), tuple(range(-16, -8, -3)))
print()
print(range(2, 8, 2).count(4), range(2, 8, 2).count(5), range(2, 8, 2).index(4))
# In[24]:
print(list(enumerate({10, 15, 25, 40})))
print(dict(enumerate((10, 15, 25, 40), 3)))
# In[25]:
print(list(zip([1, 2, 3, 4], [11, 12, 13], [21, 22, 23, 24, 25], [31, 32, 33])))
print(list(zip(*zip([1, 2, 3, 4], [11, 12, 13], [21, 22, 23, 24, 25], [31, 32, 33]))))
# In[26]:
print(list(map(sorted,
[(1, 2, 3), (7, 5, 4, 6, 8), (10, 9), (11,)])))
print(set(map(int.__add__,
[1, 2, 3, 4, 5], [11, 12, 13])))
print(dict(map(lambda x: (x, 2 * x),
(0, 1, 2, 3, 4, 5))))
print(tuple(map(lambda x, y, z: len({x, y, z}) == 2,
[1, 20, 30, -4, 5, 60], [-1, 20, 31, 4, 5], [1, 20, 32, 4, -5, 61, 70])))
# In[27]:
print(list(filter(str.isupper,
{'A': 1, 'b': 2, 'c': 3, 'D': 4, 'E': 5})))
print(tuple(filter(lambda x: x < 10,
[-1, 20, -3, -4, 50, 60])))
# In[28]:
print(sum([3, 1, 7, 5]))
print(sum({3: 1, 1: 1, 7: 2, 5: 3}))
# In[29]:
print(min((3, 1, 7, 5)))
# min() accepts also an arbitrary number of arguments
print(min(3, 1, 7, 5))
# In[30]:
print(max({3 : 10, 1: 10, 7: 10, 5: 10}))
# max() accepts also an arbitrary number of arguments
print(max(3, 1, 7, 5))
# In[31]:
sorted([2, 1, 3, 4, 0])
# In[32]:
list(reversed((2, 1, 3, 4, 0)))
# In[34]:
print(any([0, 0, 0, 0, 0]))
print(any((1, 0, 0, 1, 0)))
# In[35]:
print(all({5, 2, 3, 1, 4}))
print(all({5: 1, 2: 1, 3: 1, 0: 1, 4: 4}))
让我们开始
一、 表达形式

二、大数
超长显示
总之,问题不大。
Python 3.5.2 |Anaconda custom (64-bit)| (default, Jul 2 2016, 17:53:06)
[GCC 4.4.7 20120313 (Red Hat 4.4.7-1)] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> len(str(2**1000))
302
length
>>> 2**1000
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
较长
>>> 2**10000 # Are you serious?
19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887201298643660768551639860534602297871557517947385246369446923087894265948217008051120322365496288169035739121368338393591756418733850510970271613915439590991598154654417336311656936031122249937969999226781732358023111862644575299135758175008199839236284615249881088960232244362173771618086357015468484058622329792853875623486556440536962622018963571028812361567512543338303270029097668650568557157505516727518899194129711337690149916181315171544007728650573189557450920330185304847113818315407324053319038462084036421763703911550639789000742853672196280903477974533320468368795868580237952218629120080742819551317948157624448298518461509704888027274721574688131594750409732115080498190455803416826949787141316063210686391511681774304792596709376
超长
三、小数
Question:一个比较麻烦的问题,如何解决?
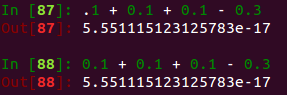
print() 函数
数字显示问题,版本变高自动改善,或者通过print作为替代方案。
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhQAAABXCAIAAADTS0tZAABCGUlEQVR4nO2dBVhUy9vAD9ssSy25hHSHIAiiiAIGoii2qIiighjXiwlioNgKJgp2IXZhoDQCIiWolHR37rJs8+0uIbWA/+t39d47v4fn4eycqTNnzvvOvFOI2I4YCAAAAACAHwHxqzMAAAAAgH8eQHkAAAAA4IcBygMAAAAAPwxQHgAAAAD4YYDyAAAAAMAPA5QHAAAAAH4YoDwAAAAA8MMA5QEAAACAHwYojxFDzAh0DKa5eWyYLgL71XkB/C4waVQGHI2Gsy9Z3EsU/Fdn6W+BXvI+yOfNp3J554duowV/IFx9Uh5koC2O+gtp06rfn7jzNqpKavf+TZNxfyGifxfsYjl68010nfz+A24TsT8rVnJuRpWknoroIDIPKI/hYdZmJhYQTLXI5dGpJEdYR0NuYr7kWFPR/4aUAAwBrejw+n1t2y8f1UAzKp9O3ll64pL7BP5fnau/A6SC2fSxd+5EyP2IsqSX3zxzu8XWPvPyladfy1oQ4sqSGBqJxEcYu27JLHP8SIURStrMUSv44Aex30ZRM2o/vzj4MCb+W3GNgN7Gzdu3jxYekDVixCmvvSUYSUGsAAaFhPPxQSw6UnOr23yDnyTo2cWyQuvOkTRZTH9BzyIWx5x+EpeSn53aLD5vjcdJK5nBlTervSDl1aln6Uqr92xVQXfGCi+5vblq3TUb6QGvZ5j3xWiqakZJiQv0yw2DWNyMGCXO3z+TvNwHh1aa9to/NDG5rJGGJYy1WOBhqyeFHEGoD/cOhOZRFRedX6Un3Dvx6pi9N2JL6RBGwf7kCj0R3v7J+Y+3389qYXX5gOF0t7vN1cPwSJBa5H/U80DLWK+lIsKC2MLHXn/cSBBYfjl9rQavl06u+hj44E1YflULUlLfZJbnPNNRf6WhBfhdYdQlv6Ia+o1if2bMmvTYBq0V+v8JzcGFSa4koVS1CCMVfayWsIsn48ftuagtBtcQIbsu2S13/MVOU2FazdPTG6dsKo+8vHH8SONi1pU3IuR0u+Tbr6bl62332FF7d506C5Vc3Ou2fv9l8zvbzPs9C4NYVA9JyxDkcRgMAoFGIdtz3oRrLtH6aV0ENszWeiJGVluxryhjtWYGp6EWu3ntQZOi/ddanvCfPvbQzP69RVZz9ouTkWWtNe/9E8Sub+0RxAjVqfOEN1+PmOA5vX+QIZUHszbcwdm33u7gSxfTXnqHWRa+f7Rfs4vPsSOmYr0i4OXOC1p+6NXjb1v4IKgDyolPiXpT6Z/spjdEF5hFLgq6cNA1JK+d/UNnou8qvV43ibE3Tx1508i51DTyWa4nAuPpn1qTfONdArknKD9lyRreygOtutf/isb9G/svhZUyIc+3Zls9A7dN4ak52G8h9NzeLfHt3B/ZCakxTwuPfPaYIAlsXf82mJWf4pq0nfT4OR9ofEyt3my1HzDg/NOhVqa2iJjJj1BbsuoSzu4kLQobL8ZpklPrMxv55KwJnMAoqRn2U2Vfv3tQtHG8Ds/wzUk+JneNov1sZdjfEYuUk9kkpTNK+G/+ppjEL3EhzxmTtlvL9lJbLJbA2INrdJU4AkRp6QLTXR45WSSWObZv5hAyaw6dXdMTpun9ijjDI/N/rvqjFuW2SOrI96uEMCE9l3mdl0JG5gZSL2vbWQPDwkS07A9qsapDswK/KCn3bv/zq85TSD+W0jTdUrRvkCFlPFzS0n/LJ5tD280ad73dbqPe9aBweUv3i+nbHHe4VXv6XraR75a6vNx5gRu30idxrbYpnvYlZO/4Uym5oa9SnfQm85LKtGK/Lc7bsyE1LUJBdlW/x6eVhe5628gnoSRcV9Q8Av9s5Gf7PJ4ji+zogOA4laH0P622JDctv7iCyfnBrCtMzc75aqhsKcXjvcNEpjm7X7bXWaCHzX51dMa5jzXh98JczZaJAe3xL4GYeXvzwwIyu3H19Uut2OO13iHsZnVKapMQzNchTnPbHw5G/SQquxVT3IxXkBFmNuVWdSgq4LuqDr21oKi8TVRZV6LT0sBsLi+sF1EikIu/NGK11GS6bB+8gvOE3lhVWtgKiUrIKuG7bBis9rqswjq4rJqWyOC9exalLquoRUhReVS34GCSq78U1jLFVA0I2D5GGGZ7ZXllY2NuAWyUS6+vgNZakVlOkVRWGmg3gdqzfQKqnI+bdH4ErPbKL80YNUXRzg45o72lnY9fUoATR21pFUtaQZp7g0UjNrOweAw7cVLy2wycqZN4Z8TUyvhKuMYCAoaT7fqsUqq8iux3OxGTXFJYUMYSN1Al4LodGcSKHJKoNgELY1Eqi0vbJVVUuu8NWzKdGQ57FXzicVS+uMX2dYJ9pSZMVEm3R6yyGHQIJ6eAHfpjJ8XdCCyxOWbNu61Ba63MrSRCghIqBDwnMgaxoJQoqSgjCGOR64tzqZL6srheL4XZVl9e2NqYUgnTsJPiLXiphekFQpOcLXimSysvbuQTn67Qp4ZhVLVRSbGFREujvuGG6SCgVabuiBcTn+NxeFxTY6j3EhNBbqGgZZduvyAt7ml3xLWm6eSDxdpdQ8i83HmAlTEw5fxHqWioiUMpJLRQf/tYb1AEG2urfLtle8Vu6eysau59i0WMCbr9kSm22tki8Vi38hjCf2eRiMrpqaoMp+HYBV4acNLvKm7Rlb2tO/wphzdIBvid3SSsm+Ssxkvj4FRtOpsYphYTVc99TGUxB9H0gH8s7EbaDHMCg5rvl6roPMvSmJ+PUvw0vHDqVqvRovwy8n1FEK3u4/EzJ/amqD+7OjfKa/vpjtWZlx21UfTS+OCzuTgD8aJDAV8Xnj6zqv7dtciQ45Fw97XmrKbWgg+voiQ3JB61V2weGHwh9Z6nY5rutSOrTfq3+1nEgvCTb/KZAlDak3sRqvvKTllLQrSCqLuB+UyoIvpS3oSIa+uM+ikfWnXoy/C05vrEiHelU899XKmCZjZFBV24TtKcqS9SeP/kJpktL10N8Jxvk/It8ubhZJqSglhd1L0cESfVzu+HXhMS/ChFUE228NaOTMuoC6sN+3xXrJqEKw8Ii77IdIkbSm1eKSRuQ+Dmg1bxIDiWabZhmRzl68PdU84nsaYezdw1XgJGjvFdOr3QOeeo4v0rt86HN4m0395IMvNYaaXQUpDcIjZ3FKo27abr6fvPSqBFxx/cN8VxbCVpQdvfkIzN9CUqH6w7I+N/1HUSri3p5VWPy08yTPzyN8L8T57yjSuBLE8Ue5sKD1sy7K+/4UvQw2C/11noMXZbve8s0hAZUmQSk2JyhCftGTfkMD6t6MnmBB3f67KDRsUiF9y99zqDhYO+PT6Zqnrvkd+06pf7Ai+dyzcNC94If3pi4/24LMgq9L73dG4q5LIIn9vJFIIioTnyZKnIHrlBRRqjuSonNOxdOH3p6y3jeVtBqKX5zUKK8vg+jQUYVgDVVFrfDkE/pDwgTvdjzOqwi+Irtp2a6N749Ng6206LFFzUytkvUezQ9NMbrRoPvXI1I3RGxct9UFi0xobakqKUwEsPiyH8XKfZo4eS5WjdhXsCIKglqf8NWtmrXaHNSL0t27XI80fgv5PyhFs7OjQNR09aNEZmKKWFVt7hG/SHsAzs487VLRS08b7IoDkNGOkR2CrpRQlhX9n/lcYbCYJux78HAVnjhbJQ29dMHznb9TOmqiCoGVfuyFnbO08daIWglJYJOMw3vV6OLQ3/Zn3wyW4xYTEUqyn9inO40lUvG9m6F5cvfqin8IlrTHWsenMwjAbpLTqui6NME9R3efyownpR48DgtI80Op3BYveZ+9GW/9Q9RNBzw3oVVFNw2vMiA2Vhttioeu36BO3v56CBdNzZwBDpl0V65a0Tfrl23j76OJjzn1wn2td7u92qViRsN2UrDJYG5cVSv6uzrm2XZ+W/POz0edL9HdajENR00stHJWoySG7T7cqRu0oet23Ey1+EbE9sbuvXVmI1vXucpTF/n0RPPqvyq5jUrKhHRzvqvmYXtKn8+X6ltQKj5Lnc5jiP0wa+d0NcTJ0lsbqm6gp0GbyY4ZYFaTdjYd7bvRZyW/gt5V9K+RVVa1+cKTO85K8rtOIAgyvsqIX35vtVeV3YbiPEyTc53mHDq1mpM9qIWrMXybxpVmy5+qBh4tYLZtjli2lQxzAlw2wqiD1/915AEslg2iL/K/smSQ5vYaIUPtufaeh7Vl94CE/M+scXH8IXXbQYVMG05/ufC8Ev33BCFlUbnhpQZaCLaS0ga7lYytwgKTa8ul+pvy1OB6vlTet8+9TykJWHv8z33rFYCkHJI16NKTUUG6z/RK2OjPsYk/n1PZE+boqZqjIPYyOtPqOKThgr1e82jUKFkIgfHTDvBIaTGztntOjT2JTwQuJ0se5pRjCs2ljziaLvn6SkfF1qRujpufFyH0hL9KwFBz9wL9Hsj2eMxP8yrsxqDb8TlNIh7rZ2ihL8xcjDtedFncuLgqCLPtP2xey0ludZFDABcRl2l5okNd59CUsBxkIJyhBGkK3G9KvzzmRQIYm1bnaaYMD83wOjqbqymkIviklhqrq0lRdndzQ+SSTrOLAKi0tQglJKYr2tNhjVMdoVry6S+CSIRitmyXGbbpTcE2eTxnk4YXOfu99LM/c4s0dfEAOREr5UYfTd3LQ4QgWBwWFgbPkwWHCI33TN+dyB+SJleJ//NnPPDhV2ZSMXhVegDRwl2AKPRiU3ZD/wfG1y005FTKxfRWQUvT25v332B11cT55ZDXHb7jY7+o/hdjXYtV9aBVWXVEmhQaFrgjq2np88CsFRGJ8/N0tPkGPnlZwXvDlZ57oTJuXF+RNpetdOO/UfKybnP80TstHoEZbUisKaDjmbjTOnjUJgJFbiUF1pK8wxY7fdF82+sPdRNslZElNezLK00RaBmGU5KVUEqzFd7V569bf8ZpR8bJ7qviX6Ys1vi+mE5fL87Hw/vxBUN+2ClVBXvhVkUOXZlRQHU2tEyvVaJLq4zHCj4yThpptVNIXJ8uzcsIYoGUb17WP79zaYXzh1ylV1GCNUV7mRvhw+mzrV02eu2FCTwEjZd7bnmFzfIzeYvCG9v34+zWzPFVnOK8xMrcCqOsrxiwgbIcJf16KQxd/UNu4yEK4NraJIWaqzBTy9LPB4EGux/wIpzitpLPhcizdXG1QvoOXmLVw9b97sIC/HlYdHmV900BzUREepTGnAqI0SRvRzLSWJKg6cXT0C5cEi557x3rrls9L+04d26wt1lyOLmPto8bbzcYrOUYdWmAt9987DfTAwqutcnKeTahMiX73LvT9vMy36mvuknjrGorVQ+ASxyKHfHLU0ZPe7FpT+1u06OKhy+MdhI2y49cuDHTi+lozo66v8o4ve+W6zGnvfbOi8Qji1OQfVRhQ/G3Lhk8Uedz+z0BYuh32N/+6BPcD/I7SqhwFHLpW3FuZVYBRvOudAHdS6jFKWevAxRz6kykyPW/Z9LcZsXZFe0oSYNF+jS/iRcl/cquF3zIwIkdDx3jena24JvT6tiGm40ESOK3laiz9XCOqMl0RyJtr3Dc4Den7olTB1t/0cycWqSX78uEny6CjugLTi3Nubsmf4rTb6suPFNlvN3p17WsmN4FxdN6PedoyW3LB4+GivnomPDFI1FaMjSE95/LDAwGM6VzIyqt8HZMN0VoggIPKHkNAS/ukfIuLltFfdny08UKKwKJVfaZJLv9+hFufVI6RU1CXFxQY+h6DWEn3U1qwqsgnrSZHB+mWCnBVWH8rFDXS6bRiU3K9VtA4d+9kGEnCopSipQHycGbtB25Yb9BU+0VGqW8YxWhqpWCVB9mPQGnLSW1DmM+dbsr2Rit5Wik7T45b6ECWDkN145q7W6/sn96/wl7HYsHiRk4H0UDqkveDiqWDm8n0HdIc0MjAqrp99KbL46qTBXiatPHR3itpxZ+4rbEw6F9Mk76rAEYf0hpT8Foye7UZDzgN8TaqUGqsng2D3fR+frjS4ZtL1Sp69yIYrOUkMIdLhYpPN5Tv8s4oo0KDKg1r3LZ+Gd5TuW39ZpM8ZZH2HUQN6SsMpD2Zj6h7PnUdqTS9c2O32vbPDrEm9audxp8x0S4KXve53XcfLnQf8yiuWKXOC2WtbORyPrYkNLnSfpM+NqD5mzcY9N6oQhkv8IlwNBlui0vVktZ+jPrH/f/ZVtfbt6i7nHJWx//AyyGfAdLQuYFgJZU7jCD91waYDUdGrs0jpOfVUM6GfNfOBVvVu9daz4e1wY8eTTx00gMnqXwVK3sX74uqaEKvNn3ad3ztdEKqL9jALs31/yGIQUciGXpuYy5zgYKnS9bkyG4pzm6Smr7WzU+799bWXJTRKTNPiduuZda+eZ46a7WuGHRicB8z6sLBSOUd5Tr0m5wQ+Sm3BT9PrGkTm153jna50Z/6OE8s19BIWyn9vQpKLI2sELQl9Kj6ttY6EVhXpbj2TCj98xhp7yba+/9Qou0RegOuW8PDeB5r0Ull+dlYzc4kK0+xc7GR4yZIOShsNicPy9STQ8LWSLmkqyUM84IzNFZpDS4vSconTluqxs0Ypi8jr0J8h39WfoVYnl7CMFjtYcL4rSu7HbH7DuUrsRyK1lLejDXpGkcmFrwqwUx0VsWxVmp9Wr7l8hz4nQFtpYjLS0E0ePUzJsKUEv8zU+e5T57pmJzzzveF+mKjkMH/x5qmjZQeKCbbmOH2rwW7nAYOByzv60JR6ZXeJ6Z1Z8oNZIpiVKWG5EsvVOTqMnPLiUUQbfrkyJ0IWMT+yRdNz6WiOGGwvfZ2DnDxHHgPRczLSasSXaHB1XkvmA99MmsIUmaFHW6rKW2Fi4+V4SLq2ytwKpIxu304YqzkjqEZ7ncFAU9zQU3UbEjb+sesKn+3Di+4LpHsqL7M64fQkr5d8tgcS/5ys8L1O83IfHjgah2PnhAnHdJd9c+azoCr2f8an0NAMJwPuFCzK54en9qQ0U5uzOKPfBcHLd0ZKG6w6oWc21wjXyrUAsshlMTl1LNSoSaNVJBCD+7/ooCHQkzCjtayVkz6BIPQj+R0Seqm/9+F7nDnDAqTEc1M+MBgMhJ7T0VtW4r/LkibAX4VV/zWmTGW2Mad1QkyOLlKcqM3TOttWEN2stNzo+xgkDAajNxWX0SC28mA2fQlKQthN1eKvyfnWIbtWEsUZ9U285keff20JdzbHgOBtxe9ORkELl0zT7i19Ga0lrRQiicpiUF7fD6dIC+L4tHDf4lMkRdMTyTPtjAn6SwMc45a10fsMlPDBkB2tRc00tkrkzIiKCctTn2ElrSJBqapncN0Y1Q9vpxisOTuRvz2awWxraWdxhMnL53xyUmJiqu2fnubh+WCM2pLadkhGkJ3zL2FvEROWafVpL8EFJCVhFEpPwtTqT/V8BGVJHuObMLyqvmR15Pmk8Zs3cNrUzNaChGax+fKoxuzoWIFx9oKl8S2KjhMIHAlHr45IoRit5k+Myzc2JOgLU4pauvJdEn07XG1tlD6WY//5WKFgNY5jbYNoRcnJbRprBDPfZ8hLJH8g8SyZ79nBapkvvWK+uDE/xv/exQk3WNPX+/hbSX0XnO2FAaeul1uscSGQSytaaXRa9dfoHO3lrsqs7LB79zsst09T7BI4tMLzZyMkl1yfNrglgtFQ09JGJrWzGOTEe3dp0qL8fCb830JylCaSE/OlrGdIctKkViWFtWv4YDOf5asoUhkMSguRBUmRMq7E8amKihFkKVGx34zN1btnKtEqckoQqmqd2WXUxB5+S5+3yU6bU3bt/bPH7vnklVPxkxX7jv2Uxjwunug6Cz8wz0NP1RVStrHd5DDT3kKkt9yD45VNnDdaO9tzuo0jcOcFNfvd4zdMeS3B1vdPA15TIbiqrZNK1z1h9am2QqnPWyHlCZO0u2oZoybr/YtEUpcPSkFYYgEOOfusw+onft1ueZd019wpUF4avN+WACOFDeqf3SPMfBNULKAkSE6LvHOgHIIkbT3NBimb/xFmW0VTZxeoNSevtdMN3kQbvGoC/pGQkqLLVCdzFQY5/8k3vL0Lz3mFbWXpBSJjjL83SeEEY/tpAUfnbaMsUUFQ+HU3rpjJblHWln4tIZNTv2TA6xIeF6gF+tgb8g8anJofccP7FgyymLxPpVcLESk9URt17NganSdaS9w2TSwJPVLw+k6z5wG5b4euHT73Zd4COXppo/VZl76SAae/cSJ8/n4PPkslJAVSmbx8BwGJEHc6arhzz/W3+ycI5MS8iTPYe2+WDAJGnj5O4sCVnTaZ2rpj5m3SiT/3OOV85KQLTqNYc0w8jnnZUKz1ETQB3Xl7bAf0tAU17KVvZjYy5gkiqFXx/vfuRpKZqLCbh2GzN01TGyhIUXg5oaYIlNXuzpFCZntrG6XozCHvIhvHw3Mw5NxvNWJjzcW5kqutMKy0/tuz8MVbVwkL8O1xNbS7eu12h7lwafSNzwZB+2Zx+nbUiqhchPlc7vp1FjEtqbSq4vFty50Hkd+8hyiZ/sDxqlZ7dlvtbMyNq+1V7Iyau4c3u8W2QG9jD38vVas399DsFxV847oPDJo/eZUeJwSrJj7Ap8rsrr0Sj4SQivra/HePGTk9MbFaf1q/9GZQwfV3TdfXaBbfykXpz+WutGM1fUvKaaw4987qylq8pMk4uZtX7LZnmSqP2TBPN+Tx4/AnkfO3OH2vi0xi4sMDR/kXHJiuBJUl3XyXq7DxzKHOViy1olf2WM3fwq8lFce/LmdQcm/fv585fqaDKncYjPjp0AvRgyd0B+vQDG22QkrPWTZ/oDNKeuLOQZx5ug8OverpnQCvkq5fAqqzLvks75nhhyDYPnlgkt8IH0UQ7R5/xE3d97pj34jj5+mf/P7N5T9CGjt/IOWtz3pvmP4TRyUwWicfxJ78adEBfkPQY1cfvS7NbXAglbYd3Cs7cO+GbgR01n841SHWS2Cw6/azYO2EnAaMvJYxodOQ3l6YWS1u4TgOyZIet/LKnO9rtAYER4929M+zgY2S7Wv5gAnP3Hn90+xqrLKWuiBfG+H05z+U9PDs7rTMo2C15JxymqiqiYpY/8Y+XGzenrvZX7+WwAjGmopd83SQMs7el6d++5rRjLJeuX9D11gFdrzb5S8T8ynSWmOk+Ttat8bdxI9RFOLcsz1UoP01uQGlrqWpNOiwAEJuyRyxVSm1uxRk0IQJW9zZf0MVLq2hVnrODm+9LnmFkp/77LwOSUbboNOcouX2+QoT3plVIZOA8zdE1ZQ7Df3KM/cnj/2WkN+MGbPqwdzuMRa0isep03Qh7qPDRGZuOZchqqk/bMnwAIXXsML3fjSppT4hSwf3q+p1/q4TTKpHxaMV5gcdV5jN0wQPEzPzyLgyuxijYiIvyNdOiLz2h44Knh2atex0BEOIa7WDSZhtjb0masx1h3TXJ1+3yKBJm6hLC3S0XvC/Ja2m2GeTF7jY/D3Xp9SUfCmtoynZBvqu+d4IQffOHkxEfdoWdWjLcpc+OWIRo27cpDvtWzi40eQX7m0Fw89y8xTIK6/nw2uoj5lprNRvsygYv7i67I9FiZSyPOkpSxQZPaQuQCpbrzslUdYAw6ur6k0zVh/BnigAQG/Q0opKXZdIEU1lkaH8wvglBwyGIIQULUwUv/9mkbJyiIp246aPFe9fcwcGR4mqDvpdoMQNRot3XgpIq/fsvgDHyY4z5v0hwQU1R5tp9k8UI69pLD8g07oGY7quhRRNvs8vQeAVDaYrQryBK89YbbLvSfz0jYPPT+0NueBuDGbbCsPvMhaGVdUz6BMdsltSwHDqWr1jhGElNadI9n8YAXzPJGG4mIpeT3EOUzJ/GbSonMr3XzARZdOFykOHQBHUDLpmcvJLG3YHhvHje3IJF1YZ/330AYFXNrDsuhbS1hp0yg9CWErFXEpl4I2+2RsIvfDdxSsSGwMn87K3/0LlARfSN5uhb/Zzo1Sztxl2RhRS1tDmT8OfmS4A8JeglMfXiZgp4v61Uyuwo73XN72oaYdwPIbJWaSMiLepcGR2fJ7uyo0TwCSTXw6lMgO7MNBGibe6B7vqAgC/GGZt5sdCQTEoKfQ+a9J8HdF/5UcpoDTZYYjbHbSqovSQJk1X1002kmBV1G8ARmGuxdA+/pX1FAD4JwGXHLsuauyvzsWvBY63cfGx+dW5APwIQHkAAAAA4IcBygMAAAAAPwxQHgAAAAD4YUagPChVCaduPX+Z+S2HOe5B4E7r/+HQYBbx06tA93sxyTV0UQUjF1f3XSbiQG0BAADAP5bhRDi19Nl8N79oGVvPhX94SMvwPG6PC4tc8uLp00dfS2r4xI3M5++crsldusFqTDk/0zfFcsuhgNEdkdf2bdjnq3Xn0EIxiFgcd/FZVFxpI01AdsKURe4Tv89VpNWlXLj/JqKoTVR1wqblM8d2T90D7r2Km/jhQeCFPKb23A2eg64ABQAAgP8vhlYezJrgM/5v8I4fz6wdO/z5FYyiN0fXhKBnjFNRrv7geywsvPFa3HJlDETJik2qkbffZaOviYLk5psfjE5OqaMtFEO1FUc9r8RM0FYtS4vYuzfyo+eNZ9xj1qnlLx02nXwvb+uih/7w8oRpfGHExU2WgjDg3uneWdzUkucbAl98YkHjTNZ66v6MygAAAAAjZUjlwaiOO5/WMWX3PKMRndKOUJrtWzoHi2XHyVhgsGHx+pdhmQtdjdBIvBSOVZ0WW+OgI0tNj0+rxqmZcc6ZhElP3hc/mRuUOkPd2dnnxae6aTMIUMvbSxeeohcnHnMz5YfIFqKjXe7ujlocO4sfuHPcZ0tzN15tCLl2r0jXdkJuKPMv1wIAAAD4QYZUHq2FSdkdCp6siD/3xH8i481nOHlZDbUKFobEdmkZBE4Wj4aIcG70SPXpKxc+3L9+3ZY0C1rwG/ryvZtm9dtHDoYUQEA4vDBnGytiTlAqSW3e1NHctahYRYsFhNtnP+S1WqKAO8d9trQoBLV9e+T1QWTjyXFfPUKrR/qyAQAA4GcxlPJgNFbWkDuqTge+XzDbbFLxm+M+btnQrcdTht8zl9mQfCODKmM9Vpm7oRtC0vrascKsdbevvIaw+i7rx/YaLWfRmmpyn90/s79Ky9PLkC0WmaTyPBJcVkmia3gFKaYqDJHr6ptaWMCd7d7KhEQ7qu9feto4wWuTMnzdcO8CAAAA/h8YSnkw20g0CMLYex4OMBKEGJOkKpb+ERRZMHmx+tAjJdSSgEPHnrLGXV+m03kaE6M2cv3eOyW6y29OaTp+7pL5ZnLs2TXj2V0Ycobr8k2XGthe4Pr2ux0UOG1sJp3KTrXn5BgIBsei+CAyk0anAXe2O7MDavkStO+r3LbLppJ8KUO+CQAAAPh/Yig1AENjEBBccZoqVwUgRA3V8dCH2ib6kKFYLZGXPDemirgc2enYtU9167sA39vQvJijaywEYXNUsAabgr3i5obbSMAxGt5nb29ua0iPD3a/uX8iBftlp5koVgQHMZub25gQd/9gBqmC2IESExcTJAN3trtwR+nVgDdM6yMuo1BQ2199/wAAAPA/MZTyQEopyQsyy4pb6JAwEmJRq6qJcDF56c5dy1jt3xKeXs0RmDl3poVYTyyUzCf77B+1ztl28cz47mPgqbWJuUQRnXGjudOEhJXHmeEeplSwI5WAwzAEOQUCpKCtoYIrWjIn+nn8RrPZAgqmEtDV5LxGexkJGFsZZb+t4NO1VRUVaAHubHd4VvDJnA5xyShP3ygGtSqpndUWcnZNySSvVZZKYG95AADwNzGkAUpYZ+ZMQQ+/a+Ezt07CfbnjnYqas2eiHFcnMGveOnoFJEHQ5SrZoj3G3B3mGRUxfjbn0oQsN68m1LxPqmSwUAo6htoCeF15THPam5cVBg6S5NTI52EkMXtD6b4rRpB4YQzEYrE6IIhfxXGq3Nm7gXtiFQ8bMl8FXopETwy2JiD4xYE72x1D1Fowpa2WSW5mdzsYdBpbjzNoFDoTnFQIAAD+RoZUHjBh0/OHVi7YfUR31hEIErVe6XPBoqs/AccpjlOAJZXwG2p1j+hC5I/Pw8rZ/6POzI7qdBFzPfc0QB9v/6fHut1Hly+duooPosPk5rkdOmHAWdTGpNP5kEhOqzrvtU9Eg/jELWac43QxxisOX2vc47bPMZD9Q27yudMeCzjJwoE72x0mNuvsnlldRU6Mm/XxS8PcbXem4yEAAAD4+xhmhTlcbLRz1PNldTXNcDEpfO9t9gUNzlx/7dUGFxdCd8+6FZrnFzVo+xclbXXxysSjtRXFbWh5WXY8nSGIbw86zEnBKAvTiyuaRMasfPznBKlO1cSvuMrztpN7UwUZI4Pn/z65C7gDAADAb8FIdpiCoSUIUoO4w7GSg557ODhIYUnF0X1c0HoLtgXolFaxRDW1jGboyQj0W/uBEZUfbDcU4P4djNrWnV4UbQEetwEAAOD/iV+5PSFKXm/yar3h/QF4gpSynDLtV2cCAAD8BwF72wIAAADghwHKAwAAAAA/DFAeAAAAAPhhgPIAAAAAwA/zX1cerMbs2CRhMxsZ9K/OyS+BUZX+Pl9+4kSx/3o9AAAAP8g/T2gwG7PfnHhdoWa71ElL8C8ufWgreLTgz/NR8uuyLizVQg3v/7eCmBHoGExz89gwXYT3LvlDQit9MnfL+TQVpxi/VWaC/2Mk/3GYNCoDjkZzT8zkXqL+DctxmM1xz2+ejvxCm+T1cKHST29Y0arfH735JrpOfv8BV92SFwcfJaRDFpc8ZqmA/XX+SfzjlAezNtjv+NFvEJQjZR1grzDcl0otf+cV8CJNzvXFOr3+J7WSP+/2Oh9FkXdfP0vjn6Q5mLWZiQUEUy1yeXQqyRHW0ZCbmC851lT0h6UWSnbKHttHs0Juzj6l/tVrotS/Qez9vdCKDq/f17b98lENNKPy6eSdpScuuU/g/9W5+qu0J98+7C/tfufowlK6RH/NwWz+GJMKjZlsKvK/VxeUtNkKrTtH0mQxMJiolvUM1M3LtTOEgOb4hzGM8mA0VTWjpMT7Ld+DGMTiZsQocf7+jVVe7j8RuOhkWytDUpmGrcFIhF17Wcyl95/R0+kDlr5TPt3zPV0FaTjuPThGiJthWmnaa//QxOSyRhqWMNZigYetntTwFZpW+uHegdA8quKi86v0hHvdYFTH7L0RW0qHMAr2J1foifD2T85/vP1+VgurywcMp7vdbS7P4+KpRf5HPQ+0jPVaKiIsiC187PXHjQSB5ZfT12rwOu+RXPUx8MGbsPyqFqSkvsksz3mmozqVJRw/c/2+7WluJyLOHJxjeG40OAj9x2DUJb+iGvqNQnM2e0uPbdBaof+P1xzsehu+M1JiXwABg4XUB94m5wYGvVAdZf5XlAe7uFrriRhZbUUMp8NWVd4ub6IkPHwowG/FkMqDWRvu4Oxbb3fwpYup9HefzLLw/aP9ml18jh0x7W0s5+U+ApiUZipCBDtoIAaxiQgJigp23cTozPVOm8sjHhalgQSJCmGG1V6shjive0WQoNXxBWrdMpeWH3r1+NsWPgjqgHLiU6LeVPonu+kJDhEJuSjowkHXkLx29g+dib6req94JMbePHXkTSPnUtPIZ7meCIynf2pN8o13CeSeoPyUJWt4Kw+06l7/Kxr3b+y/FFbKhDzfmm31DNw2hafmgFjNoef2bolv5/7ITkiNeVp45LPHBMnOMsJqbXWddHlvzMWAMPdzc5X/cT3RXwmz8lNck7aTHlthsFrjY2r1ZqsNUVv6Qnx70PWY0dnwGeK/mbmQWZUa+m3UMn1e9UnQ9NpV07+cCrUot0VSR55TXJSymEqMoZb4P6nzD+AwpLCAS1r6b/lkc2i7WeOut9tt1Lt6sHB5S/eL6dscd7hVe/petunZO4OXOw/opac2rt7ZYH5qLvNiUHRmG0xx0p8vPe116NE2S/a+beMkv2rfZsl7B49ltfOpb/p20a752lrzoBIqJzDKcPWlDyu4BxXSi4+vX7u7yfzsAujC7YgvbOVh6BpxZJlcoruqd2orNyni2z+F3rL/Y6323I2Ygmd/69XJz8OpkJS1veX3AQPcuJU+iWu1TfG0LyF7x59KyQ19leqkN5nXV0Qr9tvivD0bUtMiFGRXsfrdLAvd9baRT0JJuK6oeQT+2cjP9nk8RxbZ0QHBcSpDHRpPqy3JTcsvruCeXc6sK0zNzvlqqGwpxcM0DROZ5ux+2V5ngR42+9XRGec+1oTfC3M1WybW+eAwqbFz54rEXM96FVJjt1kWaI/hIWbe3vywgMxuXH39Uiv2eK13CMRqSUltEoL5OsRpbvvDwWhA/4PVXpdVWAeXVdMS4XZmSTm30/lnrBDufAcscmVWs5CWDI7RVFrUIa2J5y1IaY05lR1KimLcl82kMfhQiO4KzGqvKC4sh8kaKor0hKe1VmSWUySVlWS5DarhE2K1JEQUSZgpdmlBdnunuBmvICPMbMqt6lBUwKMZxIKyNikF6e/HUdNbC4rK20SVdSW4abA9lBIlFWUEYSxyfXEuVVJfFterk8Jsqy8vbG1MqYRp2ElhOMaNbylthE0KnBpPZeeKJa0pxs0Vi9ZMYgkKYYAx9XdlGFmBVpm6I15MfI7H4XFNjaHeS0w6h1XRsku3X5AW97Q74lrTdPLBYu0uCczLfXA6qO1Uet1796uC5laT0THRaTHnN4+f8HaygsOS5YrJTwM/E9NuH/lcIWlpIiZqYiyHQGAN53jAmlryQ05/aCYxOrosUR2d8SRsu4QZO22mdcKriE839iTPuiczfpWdLLEu8VpiLUx2wqox7M4QSlO2U6O1pcfn0SHcpEkqvZuKWBkDbpsKpaKhJg6lkNBC/e11vUERbKyt8u2W7RW7pbOzqrn3LRYxJuj2R6bYameLxGPdymMI/1wwonJ6qirDaFw21NKAk35XcYuu7G3d4U85vEEywO/sJmHdJGc1XhoHp2qzhnthajFR9dzHVBazj+rCqi00xF2PKnyV17ZZFhgPhgcmojXDnMCg5vulKjrPsjTm56MUPw0vnLrVarQov4x8f1MnrSDqbmA+E6qIvpQ3IeKay6isIM/bT4KaccQ7p5rHLVmDi9p64mq4+uFP9p/sdzzscL6V6iiddcvTMU332pHVJt/1EKM6/fne8xcu01ZlXV2uhWT3nqPnuoYsDvBbIQ6jVkQde5HHTuNRSJ7dqetHNdAQvSYk+FGKoJps4a0dmZZRF1ZIfr67qX9Cir1bHKyW9GOX7gSktmPR1zdRbPdOo109d2Jvivqzq3OjvLaf7nBO2i37JODU8arZqdddDLgNt9L44LO5OAPxokMBXxee9ndnhu8LvHQu3zQseCP86YmN9+OyIKvQ+97TuQZRclmEz+1kCkGR0Bx5slRkjxynshOL0ytE9UcLwsiFD+ZvOR/Kmhpyy2uWCIyY7qu+rcA7KHA9AaiP35PhG5pwyTGrwy6Kr9h2aqJ749Nj62w7LVJwUStnv0SxQ9NPb7RqPPTK1YzQGRUvd57Q5BYeCnFTLRlVqHO1NC48q9lmktOKlUbM6MDP5Rklo89e8d2k0NU+khm7wHssq+JlElt5DIinXXy+b8gGjdLbX3WulBSVNqEsFp7WgJo/eD1MrEXrLjy1bcx3PcFozS0nQ5DSWNm+TUQWrbGhtqQoJfDSw2IIP9dp9uihZDk71j0BENSSNOCRyl7tCm1G6m3ZrkWePwL/nZQn3NrRoWk4etKiMf33iOybrPIO36A/hGVgH3eubqGgjfdFBs1pwEgP1Vfpgl6UEPaV/V9pvFGfuVX8GjpSUFRBaXEDFRL+b85Z/iEEZI0XykJtXzN95GzXz5iqgqBmXLkjZ23vPFVlYOkxql67PkH7+zloIB13NjBE0DC44eI/PoU+5nO+vMtSklIemT/lD9PXediau9+Mnj5eQRBmv4J2Go1OZ7A6eo/U0eryUCbzFG8+oigTOPqJWZ74PA6h5c3uAjAqr518jHU/tW0UctfSBhoOzWm+XDlyV8njto14+YuQ7YnNbeSaXOzAhPoAEzbY6VT6OIK4YavnKnFaflq+w3zT6+XY0vBv1gef7BZF1uVX2unibwroc3UOqyn9inO40lUvG9m6F5cvfqgnNxcwtVwsZW6QFBte3a/U3xang9XypnU+BbU8ZOXhL/O9dyyWQlDyiFdjSg3FkJymUHZxh6KtMoZSWil/5rzHptW+x+NdZsyUElQ2NZSmKeOA5vhtGZGVAoaTGztntOjT2JTwQuJ0se5pPTCs2ljziaLvn6SkfF1qRhDt8c7DfXAkZk1UEoBQ0goSSKiU2sI5drX7DEJIZLzDcoUR2kIl7Ser4CCYAI5Tr5nMjqEOR2K2N9HY/9Ci/QZHWqJnLTj4gXuJ1pjqOEbif7HDslrD7wSldIi7rZ2iBH8x8nDteVHn8qIg6KLPtH0xO63leb4amIC4jAAEkaTGuy9hKcBYKEEZwgiy1Zh+dd6ZDCoksdbNTrPPgyEERThKlNJGYY48u/9dGE3VldUUelFMClPVpa28OLuj8UkiWceBVVhcghKUUhLrU6tYVHJD9gPP1yY37VTEOg0yzKbklAYlS3XOGSwYOSvtuqsB7TAJsrXjeNWuBg6/6Zrzuf2SRREmqhYd/EbRWMTtLrfn+t9Jh2kuU2e3b+g0Ymv2qUuvpu2arS/MsWiRc4M3J+tcd8KkvDh/Ik3v2mknczwaEumfEItcV1jfzn3pfFhxGXksnFyVWyesrcWxSWFUx2hXvLpI4pMgGq2YJccJIKYnce9Gk/IUJe5YRd6Js0njPJywuc/d76WZe5zZYyCDgUjhr2tRyOJvaht3GQjXhlZRpCzV2ZWLXhZ4PIi12H+BFIJTFQs+1+LN1fi5j5HZLGuqgIMweHMzdj/EfcKFRTE5zTOlBGqLWIY240Y8iAT42xmB8mCRc894b93yWWn/6UO79YV6LKzE3EeLt52PU3SOOrTC/Pve7LzceSGoyLECs6jt7XR2v4Uf1/vYilHao0ZceYSURUc81w+GwHJSoTVTWOwf390xqutcnKeTahMiX73LvT9vMy36mvuknilILFoLhU8Qixx6hJNaGrL7XQtKf+t2HRxUOaLsCBtu/fJgB46vJSP6+ir/6KJ3vtusxt43G6bscGpzDqqNKH425MIniz3ufmahLVwO+xoL930EFqWdq0uxwL48AmhVDwOOXCpvLcyrwCjedM6BOqh1GaUs9eBjjnxIlZket+wVerfoUYpzb2/KnuG32ujLjhfbbDXZsp5c8KpceLJO96QSSmlMCRFpMdl4uLrOOYq4Tprd9odD9ILI+89rkfpOXEWCVNzgtSlph9+YtV8uH96+SoGVGhJawj/9Q0S8nPaq+7OFeSREijq3btrrOk4zC6W82z/ggDofsaqQRFjYbTyl5KaXNCEmzdfozhmlJKxcxFKDM9GKlPviVg2/Y2ZEiISO9745XQ9Db0jJb8Ho2W40ZDcxSV+TKqXG6skg2L20x6crDa6ZcJuFjOpnL7LhSk4S7CCU6tRatLaKaHdjRtDESh99IauIYsKMLZ5kv7x7jiLgN2Q45cFsTN3jufNIremFC7vdlHuMPMya1Kt2HnfKTLckeNnrfrf98HIfAj44R5KR0j6Wsv+pjlHsLTKxwvwjHsCFIWB8g8SOQLLrK5nYRu/tihRVZdfcktrkynZIvtcny6+8Ypky5zHsta0cjsfWxAYXuk/S5z5YfcyajXtuVCEMl/hFuBqI8lQgrNrPUZ/Y/z/7qlr7dg0t5ByVsf/wMshnJg/pAMNKKHOsTvipCzYdiIpenUVKz6mnmgn9LAsSrerd6q1nw9vhxo4nnzpoDFgOSC3Nb+DMd1DAA5vV8KDkXbwvrq4Jsdr8adf5vdMFobpoD7Mw2/eHLMQGD8CvO8c7XenO/B0nlmvoJSyUZ5SlpneorOqeUEKrzUph6u2wlBm2m9ua/yFXyPiEFJJa/u5GtTgWKTNds6sdIKBsf/+q8pE9210Pakw4Z5GZS1SYZudiJ9P78xmQEM5652Pmzt4ptBfnNBP0Fbq+QXptYi5zgoNlz9o9as3nJJbKSWnO1OSG4twmqelr7ex6z9BjEfMjWzQ9l47mfCDtpa9zkJPnsJ+TnpORViO+RIP7xC2ZD3wzaQpTZDitMmr1p2Yha8nv9U5E01yLFJpTlZbWPm2HMqiPvzNDT9VtSNj4x64rfLYPL7ovkO5p1zOrE05P8nrJZ3sg8c/JCt+b+7zch6Y+/PUTCjn+RCQJ4jfZOV0BTS2+8ygiMYMzqlES/8C7lmA1y86C3dhiNr1/FRLRQG/Lq2Xfqk1/fvg6XlxzxjqjoWLHiCsToMjsD+cdfdMJDaVY+92nTdjfG1Z/7CgopTA6poBkajBwdQMcjcOxS4YJ72mKN2c+C6pi/2d8Cg3NcDLgTsGifH54ak9KM7U5i5PXguDlOyOlDVad0DOba4Rr5VrNWOSymJw6FmrUpNEqEojB/V900Ph+lhOjtYwzPwxOIPy8JVP0Un/vw/c4c4YFSInnpnxgMBgIPaejt6zEux6OWv4mma08VGeqg3UeI4RV/zWmTGU2twlPTI4uUpyoPbh1lpRzJYw0086YoL80wDFuWRu9g/1VFX6tFZukjmpNjs4QGjcRX/ipXnGaNf57r6+t+N3JKGjhkmnafZpf1JKsAhLeTLop9ngoZK9ZFyigM4aR9qJQWSbrfbPZ7Cli+ju2rnjuQ6Z1sBtkjNqS2nZIRhBi1n4Je4uYsExLsGVAQgNoLyikqjt0y/K2guhmpeVGPQFYzfmp5ULjRErioyWMVGAwelNxGQ1iKw9m05egJITdVC1EcWK+lPUMSY5YoVYlhbVr+GAzn+WrKFIZDEoLkQVJkTKuxPGpiooRZClRsd/05ErLGALS9M/3MxTmjxZnB4MJqk0UufHgycdZCzZKg47wb83QU3WFlG1sNznMtLfosyAIjlc2cd5o7WxvINHn7fJyH5qWl7fPv+RYr6Ze9HJ3IiCgloJLl26+596rig3eHyvLHD+DozwYjeH3rxwo7w6W8cwnA5KaaeBsNNQEIfQo28Oz3i18Wfr6xUNO016/nmYijGH388dPN7x48VNcSIyr/syu1hs1+93jN0x5LcHW908DXlMhuKqtk0pXPMLqU22FUp+3QsoTJml3NRkZNVnvXySSunxQCsISC3DI2WcdVj/x63bLu6S75k6B8tLg/bYEGClsUP8QqzHzTVCxgJIgOS3yDucBJW09zfA/bfo/s62iqbML1JqT1zl1GYI30XrGhNoKw+5WQnwaM+ykwDzdEUJKii5TncxVGOT8J9/w9i6DzytkUatfXTt87su8BXL00kbrsy6KaPb7aGlvK3q4Yn/ViuUubpj2D+kV4mM0e30y1PyIG963YJDF5H0qfXojfDB4e5avTaBb0Pa5MnGP6+vrzkZbBDrCPl69tvLxl42T5ag1TUs2u2jzY3FzTHYc87KhWOsjaAK68/bYsnub7d/6JzSA9qrkZilrxa65F21l6QUiY4yFewLQSvOrm0veXvjmeUYLgzO2nxZwdN42yhIVBIVfd+OKmaIwanpaLkp/LndNGKvpW1JOY8W5d1ZX1uIlTcbJ3bxitz3LVHnMhnm6IY8fhz+JnL/FCdfwto1SEPim+ZaLUVflQ4qqCTQFI61vj3SwE/CrGFpcIKXnLJs/0BklPXHnIM483YdEwfvsIWdlGfnuRYCQsHVsjPUgHtEq+4Ni9w8WxZ47sXt6opt7paP3EkK4uP32W8S1NcVEmJSUhGjX8ekQSm7Ggal37cLCdj5xsF6lylEH9KqndwK8SrrCCajOuuSz3LB7thWCYPvkgUl+I3wUoWeUHTd13+uOfSN/Ul7+ye/fXP4jpLHzB1Le+qz3hunCP013QBitkw9iT/K6y6gKDnxSBOFXOU9TBvtDjBT02NVHr0tzFTxSadvBvbLSg39IMLHJj4LVknPKaaKqJipi3NoEU597OE6nXVlbjcAVj2ZuAREdQr2m9aFHO/rn2cBGyfaTnmj9FYGVs1kSYtxe8QTPxJv4MYpC7Gv5A/cMc3LyGaKjNVWkub0GRdtDBdpfkxtQ6lqaStjOusQ/IKH+sDvKWfwma7rnqwjorP9wqkPsu+kIo7fAJ9l+1BgCdwsJgu2zYO2EnAaMvJYxoTMNtP6y0xEMIa7ygUmYbY29Jmqswl1Lors++bpFBk3aRF1aoKP1gv8taTVFPDvrog4vrjpoqop/zxW9sQw/50rfzRoAvyW/vq2JEJHopTn+X4BhRAia/YbeYCI2a9fPiDvy5qaPt9H5w/qCMBh+lpunQF55PR9eQ33MTGOlfptFwfjF1WV/LGGklOVJT1miyOghdQFS2XrdKYmyBhheXVVvmrH6CPZE+VnQvr323fqJJmLxx6GxP1Ff/etBSysqdV0iRTSVhxrWheNkxxn3qTcwrNwEg14/+UX7T5ZDiaoOWtPgWEL3uApcUNGkZwgNjlPRMVbp4xWBVzSYrtjHaZCE+tJWksU/aa56j86C8Uv2HcbBSGgY905DSNHCpE8aMH58T8bhwirjv2sABF7ZwLLrWkhbq3tkEyVuoNo7AvKX8GjsEqfJYJvOfwC/Xnn8MhBS067u/mLu9fKY35Pll5x0UUL6ZjP0zX5mEnAhNXubYWdEIWUNbf40/JnpjhBG5evVp5Na5exfuU8CK7H+y7CI+SHJVRXJ1IUrR/2KQWpWS3747Vw4qiQ+XXmVnx5QHf8IfqHy4EOKShGkaZIi8EFmSf0twAnmf77zlosfZa/7n7SvIqSnnd1KLhyzwHaoQVTAvx96ffrN+zF4+53+v2Zr5Q5KQ3FMQpPxbNdTpry22QH8bvxC5YGQcT1x3/XXpc8FpWK5VGV4b/9SYFjDmUt/RZ8H8HuBVlrwJHDBr0sfLmXq8vCvb7cI+Fv5D5utAAAAAPC/ApQHAAAAAH4YoDwAAAAA8MOMQHlQqhJO3Xr+MvNbDnPcg8Cd1v/DMmQW8dOrQPd7Mck1dFEFIxdX910m4kBtAQAAwD+W4UQ4tfTZfDe/aBlbz4V/eEjL8DzejguLXPLi6dNHX0tq+MSNzOfvnK7JXSrBakw5P9M3xXLLoYDRHZHX9m3Y56t159BCMYhYHHfxWVRcaSNNQHbClEXuExVxYI4eAAAA/AMYWnkwa4LP+L/BO348s3bs8OdFMIreHF0Tgp4xTkW5+oPvsbDwxmtxy5UxECUrNqlG3n6Xjb4mCpKbb34wOjmljrZQDNVWHPW8EjNBW7UsLWLv3siPnjee2fBYqgsAAACA34ghRTWjOu58WseU3fOMRnDSEDsupdm+pXOwnJPIGQsMNixe/zIsc6GrERqJl8KxqtNiaxx0ZKnp8WnVODUzaRQEwaQn74ufzA1KnaHu7Ozz4lPdtBkE0PkAAACA350hlUdrYVJ2h4InK+LPPfGfyHjzGU5eVkNZlmBIbJeWQeBk8WiICOdGj1SfvnLhw/3r121Js6AFv6Ev37tpVr995GBIAQSEwwtjgOYAAACAfwBDKQ9GY2UNuaPqdOD7BbPNJhW/Oe7jlg3dejxl+D1zmQ3JNzKoMtZjOzfkR0haXztWmLXu9pXXEFbfZf3YXqPlLFpTTe6z+2f2V2l5ehkOc+ogAAAAAH4LhlIezDYSDYIw9p6HA4wEIcYkqYqlfwRFFkxerD70uAS1JODQsaescdeX6XRu3caojVy/906J7vKbU5qOn7tkvpkce3bNeHYXhpzhunzTpQa2F7i+/W4HhRGdHgUAAACAX81QagCGxiAguOK0zvOOEaKG6njoQ20TfchQrJbIS54bU0Vcjux07Br8bn0X4HsbmhdzdI2FIGyOCtZgU7BX3NxwGwk4RsP77O3NbQ3p8cHuN/dPpGC/7DQTA5YrAAAA+N0ZSnkgpZTkBZllxS10SBgJsahV1US4mLx05x6CrPZvCU+v5gjMnDvTQqwnFkrmk332j1rnbLt4Znz3sQDU2sRcoojOuNHcvTKFlceZ4R6mVLAjlYDDMAQ5BQKkoK2hgitaMif6efxGs9ngyHsAAAD43RnSACWsM3OmoIfftfCZWyfhvtzxTkXN2TNRjqsTmDVvHb0CkiDocpVs0R5j7r79jIoYP5tzaUKWm1cTat4nVTJYKAUdQ20BvK48pjntzcsKAwdJcmrk8zCSmL2hdN8VI0i8MAZisVgdg2QDAAAAAL8ZQyoPmLDp+UMrF+w+ojvrCASJWq/0uWDR1Z+A4xTHKcCSSvgNtSS61QD54/MwzimxUWdmR3W6iLmeexqgj7f/02Pd7qPLl05dxQfRYXLz3A6d4B4czqTT+ZBIGMRqyXvtE9EgPnGLmcBg+QAAAADA78UwS/LgYqOdo54vq6tphotJ4XsfeiFocOb6a682uLgQunuQQmieX9SgPQeUtNXFKxOP1lYUt6HlZdnxdIYgvj3oMCcFoyxML65oEhmz8vGfE37NaQIAAAAA+DFGsp4bhpYgSA3iDsdKCg3izAOksKTi6D4uaL0F2wJ0SqtYoppaRjP0ZATAUDkAAAD8M/iVm4Gg5PUmr9b7hRkAAAAAwP8G2EkKAAAAAD8MUB4AAAAA+GGA8gAAAADADwOUBwAAAAB+GKA8AAAAAPDD/B+5/Y1ffXPbeQAAAABJRU5ErkJggg==" alt="" name="Image3" width="532" height="87" align="left" border="0" />
print等价于str,表示:以读者希望的形式表达出来。
In [92]: decimal.Decimal(str(1/3))
Out[92]: Decimal('0.3333333333333333') In [93]: decimal.Decimal(1/3)
Out[93]: Decimal('0.333333333333333314829616256247390992939472198486328125')
decimal 方法
>>> 1 / 3 # Floating-point (add a .0 in Python 2.X)
0.3333333333333333
>>> (2/3) + (1/2)
1.1666666666666665 >>> import decimal # Decimals: fixed precision
>>> d = decimal.Decimal('3.141')
>>> d + 1
Decimal('4.141')
>>> decimal.getcontext().prec = 2 // 精度设置
>>> decimal.Decimal('1.00') / decimal.Decimal('3.00') // 小数计算
Decimal('0.33')
fractions 方法
>>> from fractions import Fraction # Fractions: numerator+denominator
>>> f = Fraction(2, 3)
>>> f + 1
Fraction(5, 3)
>>> f + Fraction(1, 2)
Fraction(7, 6)
In [2]: (2.55).as_integer_ratio()
Out[2]: (2871044762448691, 1125899906842624) # 精算?哈哈~
四、专业数学计算
四个常用专业库
更是有专业的库提供方案 纯数计算,可能有必要单独篇章总结。
import math
import random
import statistics
import numpy as np
高数课程
The math module gives access to the underlying C library functions for floating point math:
>>> import math
>>> math.cos(math.pi / 4)
0.70710678118654757
>>> math.log(1024, 2)
10.0
统计课程
The random module provides tools for making random selections:
>>> import random
>>> random.choice(['apple', 'pear', 'banana'])
'apple'
>>> random.sample(range(100), 10) # sampling without replacement
[30, 83, 16, 4, 8, 81, 41, 50, 18, 33]
>>> random.random() # random float
0.17970987693706186
>>> random.randrange(6) # random integer chosen from range(6)
4
The statistics module calculates basic statistical properties (the mean, median, variance, etc.) of numeric data:
>>> import statistics
>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> statistics.mean(data)
1.6071428571428572
>>> statistics.median(data)
1.25
>>> statistics.variance(data)
1.3720238095238095
numpy - Quickstart tutorial
Ref: https://docs.scipy.org/doc/numpy/user/quickstart.html
一、矩阵 (Matrix)
初始化
NumPy’s array class is called ndarray. 若干例子:
# 初始化 >>> import numpy as np # (1) 描述型初始化
>>> a = np.arange(15).reshape(3, 5)
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]]) # (2) 直接赋值初始化
a = np.array([2,3,4]) # 一维
b = np.array([(1.5,2,3), (4,5,6)]) # 多维 # (3) 制定初始化
np.zeros( (3,4) ) # 多维
np.ones( (2,3,4), dtype=np.int16 ) # 多维
np.empty( (2,3) ) # 多维
np.arange( 10, 30, 5 ) # 一维:均匀点-间隔法
np.linspace( 0, 2, 9 ) # 一维:均匀点-个数法
See also
numpy.random.rand, numpy.random.randn,
fromfunction, fromfile
------------------------------------
# 形状和维度
>>>a.shape
(3, 5)
>>>a.ndim
2 >>> a.size
15
------------------------------------
# 内部成员属性
>>> type(a)
<type 'numpy.ndarray'> >>> a.dtype.name
'int64' >>> a.itemsize
8
Basic Operations
满足基本的矩阵性质,略。
>>> import numpy as np
>>> a = np.arange(15).reshape(3,5)
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> b = np.arange(15).reshape(3,5)
>>> a*b
array([[ 0, 1, 4, 9, 16],
[ 25, 36, 49, 64, 81],
[100, 121, 144, 169, 196]])
Universal Functions
Available: https://numpy.org/devdocs/user/quickstart.html
| all, any, apply_along_axis, | 矩阵对比,元素全一样 | 只要有一个一样 | lamdba 处理某维元素 | ||
| argmax, argmin, argsort, average, bincount, | 第几维的最大值 | 第几维的最小值 | 某一维排序 | 某一维均值 | 基数排序 |
| ceil, clip, conj, corrcoef, cov, | 取右 "天花板" | 设置“左右天花板” | 求共轭 | 协方差[-1, 1] | 协方差 |
| cross, cumprod, cumsum, diff, dot, | 向量积 | 累积乘 | 累计加 | 相邻元素差值 | 点积 |
| floor, inner, inv, lexsort, max, | 取左 "地板” | 类似“点积” | 逆矩阵 | 向量排序 | 向量中的最大值 |
| maximum, mean, median, min, minimum, | 向量中元素与一个值的最大值 | mean | median | 向量中的最小值 | 向量中元素与一个值的最小值 |
| nonzero, outer, prod, re, round, | 非零元素的所有坐标 | 向量1的各元素与向量2相乘 | 元素的乘积 | 正则 | 四舍五入 |
| sort, std, sum, trace, transpose, | 按照某一个维度排序 | 计算全局标准差 | 某维度求和 | 对角线元素的和 | 矩阵转置 |
| var, vdot, vectorize, where | 方差 | 点积 | 将函数向量化: lamdba | 符合某一条件的下标函数 | |
Here is a list of some useful NumPy functions and methods names ordered in categories. See Routines for the full list.
| Array Creation | arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, r, zeros, zeros_like |
| Conversions | ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat |
| Manipulations | array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, ndarray.item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, transpose, vsplit,vstack |
| Questions | all, any, nonzero, where |
| Ordering | argmax, argmin, argsort, max, min, ptp, searchsorted, sort |
| Operations | choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum |
| Basic Statistics | cov, mean, std, var |
| Basic Linear Algebra | cross, dot, outer, linalg.svd, vdot |
二、矩阵操作
矩阵下标
index 表示范围
#coding:utf-8
import numpy as np
a=np.array([[1,2,3],[4,5,6]])
print(a.shape) #(2,3)
print(a[:][0]) #这样写,无论前后,只遍历第一行
print(a[0][:])
print(a[:][1])
print(a[1][:])
############################
print(a[:,0]) #这样写才是遍历第一列,前后有区别
print(a[0,:])
print(a[:,1])
print(a[1,:])
print(a[:,2])
############################
print(a[0:3][0]) #[:]范围明明是3个,拆开写就不对,要符合实际情况
print(a[0][0])
print(a[1][0])
下标表示范围内的“间隔”
>>> a[:6:2] = -1000 # equivalent to a[0:6:2] = -1000; from start to position 6, exclusive, set every 2nd element to -1000
>>> a
array([-1000, 1, -1000, 27, -1000, 125, 216, 343, 512, 729])
矩阵遍历
传统遍历 - 规则数组
list2d = [[1,2,3],[4,5,6]]
sum = 0
for i in range(len(list2d)):
for j in range(len(list2d[0])):
sum += list2d[i][j]
句柄遍历 - 不规则数组
list2d = [[1,2,3],[4,5]]
sum = 0
for i in list2d:
for j in i:
sum += j
矩阵取整
取左地板值
# np.floor取整
>>> a = np.floor(10*np.random.random((3,4)))
>>> a
array([[ 2., 8., 0., 6.],
[ 4., 5., 1., 1.],
[ 8., 9., 3., 6.]])
>>> a.shape
(3, 4)
仅保留整数位
math.trunc(-2.5) 更人性化,return -2; 而不是floor的-3。
四舍五入
round(2.45):四舍五入
三、矩阵形变
扁平化
完全扁平
>>> a.ravel() # returns the array, flattened
array([ 2., 8., 0., 6., 4., 5., 1., 1., 8., 9., 3., 6.])
自定义扁平
>>> a.reshape(6,2) # returns the array with a modified shape
array([[ 2., 8.],
[ 0., 6.],
[ 4., 5.],
[ 1., 1.],
[ 8., 9.],
[ 3., 6.]]) ----------------------------------------------------------------------- >>> a.resize((2,6)) # this method modifies the array itself!
>>> a
array([[ 2., 8., 0., 6., 4., 5.],
[ 1., 1., 8., 9., 3., 6.]])
转置
>>> a.T # returns the array, transposed
array([[ 2., 4., 8.],
[ 8., 5., 9.],
[ 0., 1., 3.],
[ 6., 1., 6.]])
>>> a.T.shape
(4, 3)
>>> a.shape
(3, 4)
堆叠
整体对接
Stacking together different arrays.
>>> a = np.floor(10*np.random.random((2,2)))
>>> a
array([[ 8., 8.],
[ 0., 0.]])
>>> b = np.floor(10*np.random.random((2,2)))
>>> b
array([[ 1., 8.],
[ 0., .]]) >>> np.vstack((a,b)) # 第一维度的粘结,更深
array([[ 8., 8.],
[ 0., 0.],
[ 1., 8.],
[ 0., .]])
>>> np.hstack((a,b)) # 第二维度的对接,更宽
array([[ 8., 8., 1., 8.],
[ 0., 0., 0., 4.]])
各取出一个配对
column_stack & row_stack.
>>> np.hstack([np.array([1, 2, 3]), np.array([4, 5, 6])])
array([1, 2, 3, 4, 5, 6]) >>> np.column_stack([np.array([1, 2, 3]), np.array([4, 5, 6])]) # 按照列的顺序,各自拿出一个,组合在一起
array([[1, 4],
[2, 5],
[3, 6]])
>>> np.vstack([np.array([1, 2, 3]), np.array([4, 5, 6])])
array([[1, 2, 3],
[4, 5, 6]]) >>> np.row_stack([np.array([1, 2, 3]), np.array([4, 5, 6])]) # 按照行的顺序,各自拿出一个,组合在一起
array([[1, 2, 3],
[4, 5, 6]])
元素自增加一维度
>>> from numpy import newaxis
>>> a = np.array([4.,2.])
>>> b = np.array([2.,8.])
>>> a[: ,newaxis] # This allows to have a 2D columns vector
array([[ 4.],
[ 2.]]) # 可见,自增加了维度的效果 >>> np.column_stack((a[:,newaxis],b[:,newaxis])) // 两个一维数组的合并和两个数字合并,本质上是一样的:因为一个数字其实就是“默认一维”
array([[ 4., 2.],
[ 2., 8.]]) >>> np.vstack((a[:,newaxis],b[:,newaxis])) # The behavior of vstack is different
array([[ 4.],
[ 2.],
[ 2.],
[ 8.]])
拆分
注意:可以通过定义 “分割点” 来分割高维矩阵。
Splitting one array into several smaller ones.
>>> a = np.floor(10*np.random.random((2,12)))
>>> a
array([[ 9., 5., 6., 3., 6., 8., 0., 7., 9., 7., 2., 7.],
[ 1., 4., 9., 2., 2., 1., 0., 6., 2., 2., 4., 0.]]) >>> np.hsplit(a,3) # Split a into 3
[array([[ 9., 5., 6., 3.], [ 1., 4., 9., 2.]]),
array([[ 6., 8., 0., 7.], [ 2., 1., 0., 6.]]),
array([[ 9., 7., 2., 7.], [ 2., 2., 4., 0.]])]
>>> np.hsplit(a, (3,4)) # Split a after the third and the fourth column 看样子像是"分割点"
[array([[ 9., 5., 6.], [ 1., 4., 9.]]),
array([[ .], [ 2.]] ),
array([[ 6., 8., 0., 7., 9., 7., 2., 7.], [ 2., 1., 0., 6., 2., 2., 4., 0.]])] >>> np.vsplit(a,(3,4))
[array([[ 2., 9., 0., 4., 3., 2., 8., 0., 6., 2., 0., 4.],
[ 8., 0., 5., 3., 4., 9., 5., 0., 3., 4., 4., 5.]]), array([], shape=(0, 12), dtype=float64), array([], shape=(0, 12), dtype=float64)]
np.split更灵活,任意分割!
>>> x = np.arange(8.0)
>>> np.split(x, [3, 5, 6, 10])
[array([ 0., 1., 2.]),
array([ 3., 4.]),
array([ 5.]),
array([ 6., 7.]),
array([], dtype=float64)]
其他:numpy.array_split 【似乎用处不大】
四、矩阵拷贝
引用,非拷贝
No Copy at All, 引用
>>> b = a # no new object is created
>>> id(a) # id is a unique identifier of an object
映射关系 view
虽 id 不同,但base指向对方。
view矩阵虽然形状变了,但每个元素还是跟原来的“有映射关系”,改变某值,对应的"原位置的值"改变。
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a <---- 理解这句话!
True
>>> c.flags.owndata
False
>>> c.shape = 2,6 # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c[0,4] = 1234 # a's data changes
>>> a
array([[ 0, 1, 2, 3],
[1234, 5, 6, 7],
[ 8, 9, 10, 11]])
Deep Copy , 深拷贝
>>> d = a.copy() # a new array object with new data is created
>>> d is a
False
>>> d.base is a # d doesn't share anything with a
False
>>> d[0,0] = 9999
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
五、统计采样
Ref: Numpy随机抽样
正态分布
#均匀分布
np.random.rand(2,5) // shape #正态分布
np.random.randn(1,10) // shape #均匀分布 - 半开半闭区间 - 整数 【nice】
np.random.randint(2, 5, 10) // interval
np.random.randint(2, 5, (6,6)) // interval #均匀分布 - 闭区间 - 整数 【nice】
np.random.random_integers(2, 5, 10) #均匀分布 - 半开半闭区间 - 百分比
np.random.random_sample((6,6)) #均匀分布 - 闭区间 - 整数
np.random.choice(10, 5)
其他分布
random.beta(a,b,size):从 Beta 分布中生成随机数。
random.binomial(n, p, size):从二项分布中生成随机数。
random.chisquare(df,size):从卡方分布中生成随机数。
random.dirichlet(alpha,size):从 Dirichlet 分布中生成随机数。
random.exponential(scale,size):从指数分布中生成随机数。
random.f(dfnum,dfden,size):从 F 分布中生成随机数。
random.gamma(shape,scale,size):从 Gamma 分布中生成随机数。
random.geometric(p,size):从几何分布中生成随机数。
random.gumbel(loc,scale,size):从 Gumbel 分布中生成随机数。
random.hypergeometric(ngood, nbad, nsample, size):从超几何分布中生成随机数。
random.laplace(loc,scale,size):从拉普拉斯双指数分布中生成随机数。
random.logistic(loc,scale,size):从逻辑分布中生成随机数。
random.lognormal(mean,sigma,size):从对数正态分布中生成随机数。
random.logseries(p,size):从对数系列分布中生成随机数。
random.multinomial(n,pvals,size):从多项分布中生成随机数。
random.multivariate_normal(mean, cov, size):从多变量正态分布绘制随机样本。
random.negative_binomial(n, p, size):从负二项分布中生成随机数。
random.noncentral_chisquare(df,nonc,size):从非中心卡方分布中生成随机数。
random.noncentral_f(dfnum, dfden, nonc, size):从非中心 F 分布中抽取样本。
random.normal(loc,scale,size):从正态分布绘制随机样本。
random.pareto(a,size):从具有指定形状的 Pareto II 或 Lomax 分布中生成随机数。
random.poisson(lam,size):从泊松分布中生成随机数。
random.power(a,size):从具有正指数 a-1 的功率分布中在 0,1 中生成随机数。
random.rayleigh(scale,size):从瑞利分布中生成随机数。
random.standard_cauchy(size):从标准 Cauchy 分布中生成随机数。
random.standard_exponential(size):从标准指数分布中生成随机数。
random.standard_gamma(shape,size):从标准 Gamma 分布中生成随机数。
random.standard_normal(size):从标准正态分布中生成随机数。
random.standard_t(df,size):从具有 df 自由度的标准学生 t 分布中生成随机数。
random.triangular(left,mode,right,size):从三角分布中生成随机数。
random.uniform(low,high,size):从均匀分布中生成随机数。
random.vonmises(mu,kappa,size):从 von Mises 分布中生成随机数。
random.wald(mean,scale,size):从 Wald 或反高斯分布中生成随机数。
random.weibull(a,size):从威布尔分布中生成随机数。
random.zipf(a,size):从 Zipf 分布中生成随机数。
再结合取整即可:np.floor(<list>)
End.
[Python] 01 - Number的更多相关文章
- [Python] 01 - Number and Matrix
故事背景 一.大纲 如下,chapter4 是个概览,之后才是具体讲解. 二. 编译过程 Ref: http://www.dsf.unica.it/~fiore/LearningPython.pdf
- Python 数字(Number)
Python 数字(Number) Python 数字数据类型用于存储数值. 数据类型是不允许改变的,这就意味着如果改变数字数据类型的值,将重新分配内存空间. 以下实例在变量赋值时 Number 对象 ...
- python基础===Number
本文转自:python之Number 1.Python number数字 Python Number 数据类型用于存储数值. 数据类型是不允许改变的,这就意味着如果改变 Number 数据类型的值,将 ...
- python之Number
1.Python number数字 Python Number 数据类型用于存储数值. 数据类型是不允许改变的,这就意味着如果改变 Number 数据类型的值,将重新分配内存空间. 创建一个numbe ...
- 实验吧-杂项-WTF?(python 01代码转图片)
比较新的题型了吧. code为base64码,转码出来是01代码,直接蒙圈,查阅相关wp才知道是转图片的. 复制到编辑器里可以看到一共65536个数字,开方是256,于是这就是一个方形的图片了–> ...
- python 01篇
一.Pycharm 使用小tips 1.1 pycharm创建项目时,选择Python环境,不使用默认的虚拟环境 1.2 如何在pycharm中查看python版本 路径:File-Settings- ...
- python 01
注意Python 是大小写敏感的,即print 与Print 不一样 推荐编辑器 vim & sublime 如何运行 #!/usr/bin/python#Filename: hellowor ...
- [LeetCode][Python]Largest Number
# -*- coding: utf8 -*-'''__author__ = 'dabay.wang@gmail.com'https://oj.leetcode.com/problems/largest ...
- 【Python 01】Python可以做什么
Python学习未来方向: 1.数据分析 2.自然语言处理 3.社交网络分析 4.人工智能 5.深度学习 6.计算机视觉 7.网络爬虫 8.量化交易
随机推荐
- Knockout.Js官网学习(Mapping高级用法二)
使用ignore忽略不需要map的属性 如果在map的时候,你想忽略一些属性,你可以使用ignore累声明需要忽略的属性名称集合: " }; var mapping = { 'ignore' ...
- Redis深入之对象
Redis对象系统 前面介绍了Redis用到的全部主要数据结构,如简单动态字符串(SDS).双端链表.字典.压缩列表.整数集合等 Redis并没有直接使用这些数据结构来实现键值对数据库.而是基于这些数 ...
- UAC 实现原理及绕过方法-打洞专用
首页 新随笔 订阅 管理 随笔 - 7 文章 - 0 评论 - 0 UAC 实现原理及绕过方法 目录 0x01 UAC 实现方法(用户登陆过程)0x02 UAC 架构0x03 触发UAC0x0 ...
- redis优化配置和redis.conf说明(转)
1. redis.conf 配置参数: #是否作为守护进程运行 daemonize yes #如以后台进程运行,则需指定一个pid,默认为/var/run/redis.pid pidfile redi ...
- React Native 设置RGBA背景色
React Native 设置RGBA背景色: 可以先用Mac自带吸色工具,获取RGB值,然后设置背景如下: backgroundColor: 'rgba(52, 52, 52, 0.8)', 透明度 ...
- swift学习之常量和变量
常量:就是在初始化时(试试定义时不赋值会不会报错)赋予一个准确的值,能够在非常多地方直接用到,用letkeyword生命 变量:这个就不用说了,就是能够在下一秒你能够随便改变的量,用varkeywor ...
- bindpose定义
根据常识,有: 但根据骨骼动画的定义,又有: 对比两式,可得bindpose的定义: 即骨骼bone的bindpose是:在绑定时刻,将顶点由mesh的局部空间变换到bone的局部空间的变换.
- LeetCode OJ 238. Product of Array Except Self 解题报告
题目链接:https://leetcode.com/problems/product-of-array-except-self/ 238. Product of Array Except Se ...
- windows下安装pycharm并连接Linux的python环境
1. 下载安装Pycharm专业版 具体方法略.Pycharm5激活方法参考http://www.cnblogs.com/snsdzjlz320/p/7110186.html 2. 添加配置连接远程服 ...
- 3. Tensorflow生成TFRecord
1. Tensorflow高效流水线Pipeline 2. Tensorflow的数据处理中的Dataset和Iterator 3. Tensorflow生成TFRecord 4. Tensorflo ...

