网络流 最大流HDU 3549

/
/
/
/
/
/
/
/
/
/

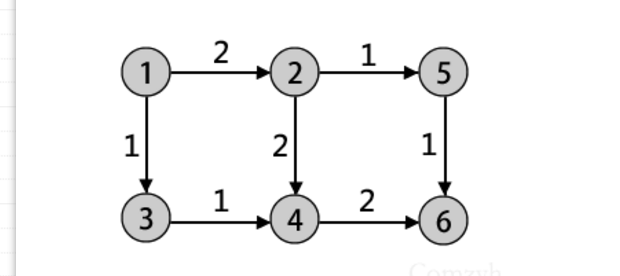
在这幅图中我们首先要增广1->2->4->6,这时可以获得一个容量为2的流,但是如果不建立4->2反向弧的话,则无法进一步增广,
最终答案为2,显然是不对的,然而如果建立了反向弧4->2,则第二次能进行1->3->4->2->5->6的增广,最大流为3.

 #include<stdio.h>
 #include<algorithm>
 #include<string.h>
 #include<queue>
 typedef long long LL;

 using namespace std;
 int n,m;
 #define inf 100000000
 #define MAXN 5000
 #define MAXN1 50
 struct edg
 {
     int w,to,next;
 }x[MAXN+];
 int head[MAXN1],cnt;
 int vis[MAXN1];

 void add(int u,int v,int w)
 {
     x[cnt].next=head[u];
     x[cnt].to=v;
     x[cnt].w=w;
     head[u]=cnt++;
     x[cnt].next=head[v];
     x[cnt].to=u;
     x[cnt].w=;
     head[v]=cnt++;
 }
 queue<int>q1;

 int bfs()  //层次网络
 {
     memset(vis,-,sizeof(vis));
     vis[]=;
     q1.push();
     while(!q1.empty())
     {
         int now=q1.front();
         q1.pop();
         int j;
         for(j=head[now];j!=-;j=x[j].next)
         {
             if(vis[x[j].to]<&&x[j].w)
             {
                 vis[x[j].to]=vis[now]+;
                 q1.push(x[j].to);
             }
         }
     }
     if(vis[n]<) //汇点不在网络 结束
         return ;
     return ;
 }
 int dfs(int u,int w)
 {
     if(u==n)
         return w;
     int j;
     int ans=;

     for(j=head[u];j!=-&&ans<=w;j=x[j].next)
     {
         if(vis[x[j].to]==vis[u]+&&x[j].w)
         {
             int b=dfs(x[j].to,min(w-ans,x[j].w)); //流进去的有2个限制 min(总流量减去已经流掉的，可以流进去的)
             x[j].w-=b;
             x[j^].w+=b;                          //cnt=0 开始 反向边下标=j^1  可以自己试试
             ans+=b;
         }
     }
     return ans;
 }
 int main()
 {
     int t,ca;

     scanf("%d",&t);
     ca=;
     while(t--)
     {
         scanf("%d%d",&n,&m);
         cnt=;
         memset(head,-,sizeof(head));
         int i,j;
         for(i=;i<=m;i++)
         {
             int u,v,w;
             scanf("%d%d%d",&u,&v,&w);
             add(u,v,w); //建边 有反向边
         }
         int ans=;
         while(bfs()) //Dinic bfs+dfs
             ans+=dfs(,inf);
         printf("Case %d: %d\n",ca++,ans);
     }

     return ;
 }
 　　/*By--MJY*/