NOIp 2014 #2 联合权值 Label：图论！！！未AC

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu

×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，[b]输出它时要对10007 取余。 [/b]

输入输出样例

输入样例#1：

输出样例#1：

20 74

说明

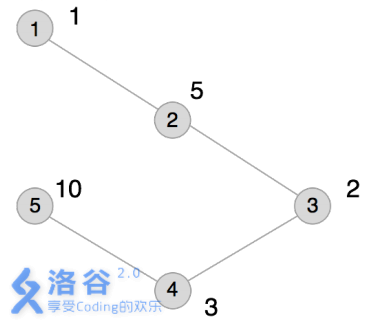
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

代码

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<algorithm>

 #include<vector>

 #include<map>

 #define MAXN 500005

 using namespace std;

 struct cc{

     map<int,int> m;

 }nod[MAXN];

 int ans,sum,N;

 int vis[MAXN],w[MAXN];

 vector<int> G[MAXN];

 int cc(int x,int pre){

     if(pre!=-){

         for(int i=;i<G[pre].size();i++){

             int pre_pre=G[pre][i];

             if(pre_pre==x) continue;

             if(nod[x].m.count(pre_pre)!=) continue;

             nod[pre_pre].m[x]=nod[x].m[pre_pre]=;

             ans=max(ans,(w[pre_pre]*w[x])%);//注意题目描述，此处不应该取模

             sum=(sum+w[pre_pre]*w[x]*)%;

 //            cout<<w[pre_pre]*w[x]<<endl;

         }

     }

     vis[x]=;

 //    printf("%d %d %d \n",x,pre,pre_pre);

     for(int i=;i<G[x].size();i++){

         if(!vis[G[x][i]]) cc(G[x][i],x);

     }

 }

 int main(){

 //    freopen("link.in","r",stdin);

 //    freopen("link.out","w",stdout);

     scanf("%d",&N);

     for(int i=;i<N;i++){

         int x,y;

         scanf("%d%d",&x,&y);

         G[x].push_back(y);

         G[y].push_back(x);

     }

     for(int i=;i<=N;i++) scanf("%d",&w[i]);

     cc(,-);

     printf("%d %d\n",ans,sum);

     return ;

 }

30分，脑洞map

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<algorithm>

 #include<vector>

 #include<map>

 #define MAXN 500005

 using namespace std;

 int ans,sum,N;

 int vis[MAXN],w[MAXN];

 vector<int> G[MAXN];

 int cc(int x,int pre){

     if(pre!=-){

         for(int i=;i<G[pre].size();i++){

             int pre_pre=G[pre][i];

             if(pre_pre==x) continue;

             if(!vis[pre_pre]) continue;

             ans=max(ans,w[pre_pre]*w[x]);//ans不用取模

             sum=(sum+w[pre_pre]*w[x]*)%;

         }

     }

     vis[x]=;

     for(int i=;i<G[x].size();i++){

         if(!vis[G[x][i]]) cc(G[x][i],x);

     }

 }

 int main(){

 //    freopen("link.in","r",stdin);

 //    freopen("link.out","w",stdout);

     scanf("%d",&N);

     for(int i=;i<N;i++){

         int x,y;

         scanf("%d%d",&x,&y);

         G[x].push_back(y);

         G[y].push_back(x);

     }

     for(int i=;i<=N;i++) scanf("%d",&w[i]);

     cc(,-);

     printf("%d %d\n",ans,sum);

     return ;

 }

60分，还是TLE，大雾

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<algorithm>

 #include<vector>

 #define MAXN 500005

 using namespace std;

 int ans,sum,N;

 int vis[MAXN],w[MAXN];

 vector<int> G[MAXN];

 int cc(int x){

     vis[x]=;

     if(G[x].size()>=){

         for(int i=;i<G[x].size();i++){

             for(int j=i+;j<G[x].size();j++){

                 int k=G[x][i],y=G[x][j];

                 ans=max(ans,w[k]*w[y]);

                 sum=(sum+w[k]*w[y]*)%;

             }

         }

     }

 //    cout<<x<<endl;

     for(int i=;i<G[x].size();i++){

         if(!vis[G[x][i]]) cc(G[x][i]);

     }

 }

 int main(){

 //    freopen("link.in","r",stdin);

 //    freopen("link.out","w",stdout);

     scanf("%d",&N);

     for(int i=;i<N;i++){

         int x,y;

         scanf("%d%d",&x,&y);

         G[x].push_back(y);

         G[y].push_back(x);

     }

     for(int i=;i<=N;i++) scanf("%d",&w[i]);

     cc();

     printf("%d %d\n",ans,sum);

     return ;

 }

60分的另外一种写法

题解：//格式优化 by Radiumlrb

一、审题
首先我们一看到图就就知道图论有关，又因为有n个点和n-1条边，不难看出是一个无环图，这对题目的难度降低了很多。如果直接模拟的话肯定不行，会超时，所以我们应该换一种思维，及一个点周围的节点两两都能产生联合全值，
下面就来完善这一思想。

二、算法讨论
①、公式推导：
假如一个点x存在n个节点，分别为x1,x2…xn.
节点最大值只需存下节点中最大值，每次再用当前节点与最大节点相乘，在于max比较。
则关于x节点间的的联合全值之和为：
x（x2+x3…+xn）+x2(x1+x3…+xn)+xn(x1+x2…+xn-1) ；经整理可知就是每两个节点相乘，最后再成2即可；
化简为：
x1(x2+x3…+xn)+x2(x3+x4…+xn)+xn-2(xn-1+xn)+xn-1*xn
可理解为把每一个点和所有前面出现的的点之和相乘再相加最后乘2。

②、注意事项：
1、因为图是没有环的，所以一点到距离为二的点必定有且仅有一条，每一个点任意两个节点必将经过此点，所以我们不必讨论是否会重复。
2、因为数据范围很大，用邻接矩阵会爆内存，所以我们必须要用邻接矩阵才行(注意要存双向边）。
3、求联合权值之和时必须边做边对10007取模，不然会超出范围。

三、算法实现
用一个二维数组a存边，一维数组max1用来存该点节点中的最大值,大概就是这样吧，剩下的变量就在代码中一一解释。

四、代码展示

//Orz P党大神

 c,qz,dd:array[..]of longint;

 n,i,tot,x,y,max:longint;

 //max存最大值，tot存联合全值之和

 procedure sb(x:longint);

 var i,tot1,nn,ny,max1:longint;

 begin

   tot1:=; nn:=dd[x]; max1:=;

   ny:=a[nn].y;

 //循环列举该点的所有节点  tot1存前面出现的节点全值之和。

   repeat

     if max1*qz[ny]>max then max:=max1*qz[ny];

     if qz[ny]>max1 then max1:=qz[ny];

     tot:=(tot+tot1*(qz[ny]mod ))mod ;

 tot1:=(tot1+qz[ny])mod ;

 //要不断对10007取模

     nn:=c[nn];

     ny:=a[nn].y;

   until nn=;

 end;

 begin

 read(n);

 for i:= to n- do

    begin

 read(x,y);

 a[i*-].x:=x;a[i*-].y:=y;

 c[i*-]:=dd[x];dd[x]:=i*-;

 //此处为双向边  dd数组用来把起点相同的边绑定在一起

 a[i*].x:=y;  a[i*].y:=x;

 c[i*]:=dd[y];dd[y]:=i*;

    end;

 for i:= to n do

     read(qz[i]);

 for i:= to n do

 sb(i);

 tot:=tot mod ;

 write(max,' ',tot* mod );

 //注意最后答案要乘2

 end.

五、最后的寄语：
其实本题还有更简单的做法，就是搜边即可，没必要枚举每个点，这个留给大家自己去想，我就不多讲。