K-means之matlab实现

引入

作为练手，不妨用matlab实现K-means

要解决的问题：n个D维数据进行聚类（无监督），找到合适的簇心。

这里仅考虑最简单的情况，数据维度D=2，预先知道簇心数目K（K=4）

理论步骤

关键步骤：

（1）根据K个簇心(clusters，下标从1到K)，确定每个样本数据Di(D为所有数据整体，Di为某个数据，i=1...n)所属簇，即欧氏距离最近的那个。

簇心编号:

c_i = arg min_{j} {D_i - clusters_j}， 即使得欧氏距离最近的那个j

(2) 更新簇心：所属簇编号c_i相同的样本数据D_i的元素们，用他们均值来替代原有簇心（D维向量均值）

代码

% my_kmeans
% By Chris, zchrissirhcz@gmail.com
% 2016年9月30日 19:13:43

% 簇心数目k
K = 4;

% 准备数据，假设是2维的,80条数据，从data.txt中读取
%data = zeros(100, 2);
load 'data.txt'; % 直接存储到data变量中

x = data(:,1);
y = data(:,2);

% 绘制数据，2维散点图
% x,y: 要绘制的数据点  20:散点大小相同，均为20  'blue':散点颜色为蓝色
s = scatter(x, y, 20, 'blue');
title('原始数据：蓝圈；初始簇心：红点');

% 初始化簇心
sample_num = size(data, 1);       % 样本数量
sample_dimension = size(data, 2); % 每个样本特征维度

% 暂且手动指定簇心初始位置
clusters = zeros(K, sample_dimension);
clusters(1,:) = [-3,1];
clusters(2,:) = [2,4];
clusters(3,:) = [-1,-0.5];
clusters(4,:) = [2,-3];

hold on; % 在上次绘图（散点图）基础上，准备下次绘图
% 绘制初始簇心
scatter(clusters(:,1), clusters(:,2), 'red', 'filled'); % 实心圆点，表示簇心初始位置

c = zeros(sample_num, 1); % 每个样本所属簇的编号

PRECISION = 0.0001;

iter = 100; % 假定最多迭代100次
for i=1:iter
    % 遍历所有样本数据，确定所属簇。公式1
    for j=1:sample_num
        %t = arrayfun(@(item) item
        %[min_val, idx] = min(t);
        gg = repmat(data(j,:), K, 1);
        gg = gg - clusters;   % norm:计算向量模长
        tt = arrayfun(@(n) norm(gg(n,:)), (1:K)');
        [minVal, minIdx] = min(tt);
        % data(j,:)的所属簇心，编号为minIdx
        c(j) = minIdx;
    end

    % 遍历所有样本数据，更新簇心。公式2
    convergence = 1;
    for j=1:K
        up = 0;
        down = 0;
        for k=1:sample_num
            up = up + (c(k)==j) * data(k,:);
            down = down + (c(k)==j);
        end
        new_cluster = up/down;
        delta = clusters(j,:) - new_cluster;
        if (norm(delta) > PRECISION)
            convergence = 0;
        end
        clusters(j,:) = new_cluster;
    end
    figure;
    f = scatter(x, y, 20, 'blue');
    hold on;
    scatter(clusters(:,1), clusters(:,2), 'filled'); % 实心圆点，表示簇心初始位置
    title(['第', num2str(i), '次迭代']);

    if (convergence)
        disp(['收敛于第', num2str(i), '次迭代']);
        break;
    end
end

disp('done');

使用到的数据(data.txt)

1.658985    4.285136
-3.453687   3.424321
4.838138    -1.151539
-5.379713   -3.362104
0.972564    2.924086
-3.567919   1.531611
0.450614    -3.302219
-3.487105   -1.724432
2.668759    1.594842
-3.156485   3.191137
3.165506    -3.999838
-2.786837   -3.099354
4.208187    2.984927
-2.123337   2.943366
0.704199    -0.479481
-0.392370   -3.963704
2.831667    1.574018
-0.790153   3.343144
2.943496    -3.357075
-3.195883   -2.283926
2.336445    2.875106
-1.786345   2.554248
2.190101    -1.906020
-3.403367   -2.778288
1.778124    3.880832
-1.688346   2.230267
2.592976    -2.054368
-4.007257   -3.207066
2.257734    3.387564
-2.679011   0.785119
0.939512    -4.023563
-3.674424   -2.261084
2.046259    2.735279
-3.189470   1.780269
4.372646    -0.822248
-2.579316   -3.497576
1.889034    5.190400
-0.798747   2.185588
2.836520    -2.658556
-3.837877   -3.253815
2.096701    3.886007
-2.709034   2.923887
3.367037    -3.184789
-2.121479   -4.232586
2.329546    3.179764
-3.284816   3.273099
3.091414    -3.815232
-3.762093   -2.432191
3.542056    2.778832
-1.736822   4.241041
2.127073    -2.983680
-4.323818   -3.938116
3.792121    5.135768
-4.786473   3.358547
2.624081    -3.260715
-4.009299   -2.978115
2.493525    1.963710
-2.513661   2.642162
1.864375    -3.176309
-3.171184   -3.572452
2.894220    2.489128
-2.562539   2.884438
3.491078    -3.947487
-2.565729   -2.012114
3.332948    3.983102
-1.616805   3.573188
2.280615    -2.559444
-2.651229   -3.103198
2.321395    3.154987
-1.685703   2.939697
3.031012    -3.620252
-4.599622   -2.185829
4.196223    1.126677
-2.133863   3.093686
4.668892    -2.562705
-2.793241   -2.149706
2.884105    3.043438
-2.967647   2.848696
4.479332    -1.764772
-4.905566   -2.911070

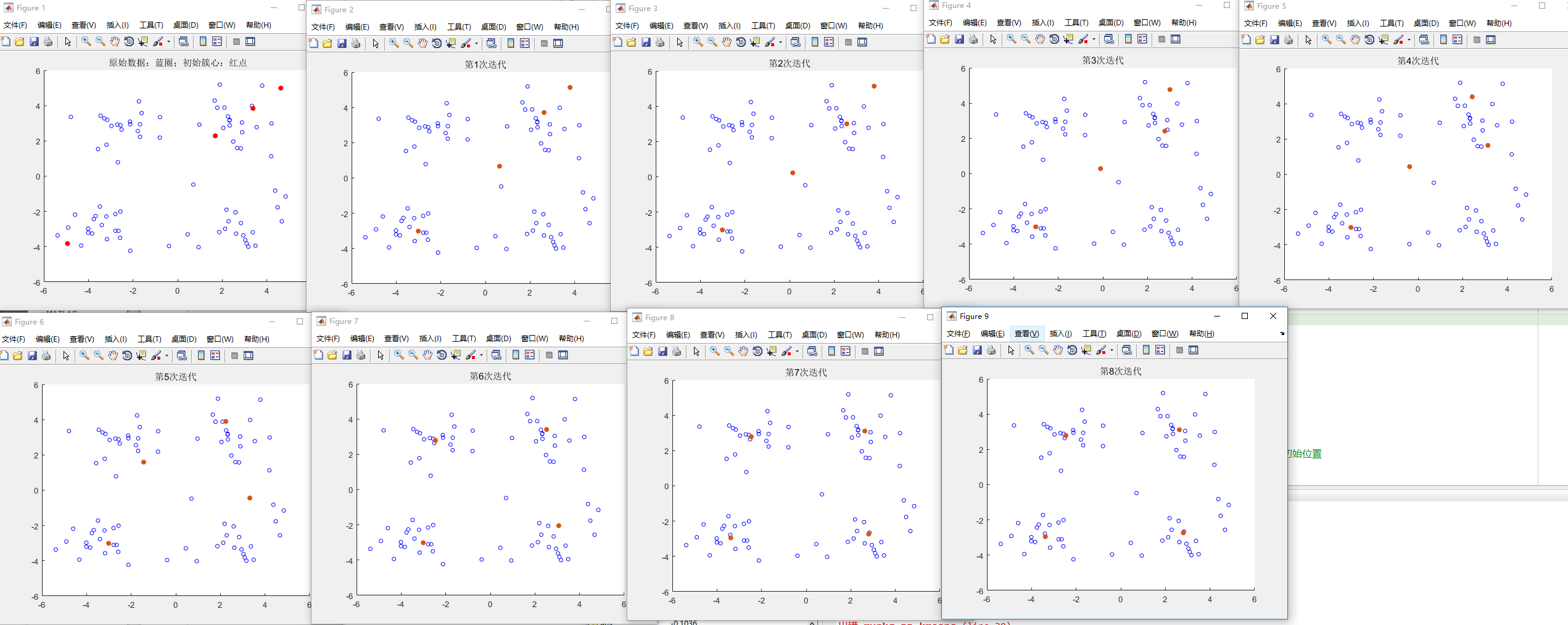
运行结果

缺点

非常naive的kmeans，对于K个簇心初始位置非常敏感，有时候会产生dead point，即有些簇心被孤立而没有样本数据归属它。

第一次改进：簇心向量的每个维度，在样本数据的各自维度的最小值和最大值之间取值

clusters = zeros(K, sample_dimension);
minVal = min(data); % 各维度计算最小值
maxVal = max(data); % 各维度计算最大值
for i=1:K
    clusters(i, :) = minVal + (maxVal - minVal) * rand();
end

效果：

第二次改进：在线K-means，使用随机梯度下降SGD替代批量梯度下降BGD

思路是，每次仅仅取出一个样本数据x_i，找出离他最近的簇心cluster_j，并把簇心往x_i的方向拉。这替代了原来使用“所有的、类别编号为c_j的样本，算出一个均值，作为新簇心”策略.

同时考虑到收敛速度，每次将“最近的簇心”向数据项“拉取”的时候，乘以一个学习率eta，eta最好是随着迭代次数增加而有所减小，即迭代次数t的减函数。此处代码实现中使用倒数(eta = basic_eta/i)，你也可以用更精致的函数替代。

参考代码:

% 簇心数目k
K = 4;

% 准备数据，假设是2维的,80条数据，从data.txt中读取
%data = zeros(100, 2);
load 'data.txt'; % 直接存储到data变量中

x = data(:,1);
y = data(:,2);

% 绘制数据，2维散点图
% x,y: 要绘制的数据点  20:散点大小相同，均为20  'blue':散点颜色为蓝色
s = scatter(x, y, 20, 'blue');
title('原始数据：蓝圈；初始簇心：红点');

% 初始化簇心
sample_num = size(data, 1);       % 样本数量
sample_dimension = size(data, 2); % 每个样本特征维度

% 暂且手动指定簇心初始位置
% clusters = zeros(K, sample_dimension);
% clusters(1,:) = [-3,1];
% clusters(2,:) = [2,4];
% clusters(3,:) = [-1,-0.5];
% clusters(4,:) = [2,-3];
% 簇心赋初值：计算所有数据的均值，并将一些小随机向量加到均值上
clusters = zeros(K, sample_dimension);
minVal = min(data); % 各维度计算最小值
maxVal = max(data); % 各维度计算最大值
for i=1:K
    clusters(i, :) = minVal + (maxVal - minVal) * rand();
end 

hold on; % 在上次绘图（散点图）基础上，准备下次绘图
% 绘制初始簇心
scatter(clusters(:,1), clusters(:,2), 'red', 'filled'); % 实心圆点，表示簇心初始位置

c = zeros(sample_num, 1); % 每个样本所属簇的编号

PRECISION = 0.001;

iter = 100; % 假定最多迭代100次
% Stochastic Gradient Descendant 随机梯度下降（SGD）的K-means，也就是Competitive Learning版本
basic_eta = 0.1;  % learning rate
for i=1:iter
    pre_acc_err = 0;  % 上一次迭代中，累计误差
    acc_err = 0;  % 累计误差
    for j=1:sample_num
        x_j = data(j, :);     % 取得第j个样本数据，这里体现了stochastic性质

        % 所有簇心和x计算距离，找到最近的一个（比较簇心到x的模长）
        gg = repmat(x_j, K, 1);
        gg = gg - clusters;
        tt = arrayfun(@(n) norm(gg(n,:)), (1:K)');
        [minVal, minIdx] = min(tt);

        % 更新簇心：把最近的簇心(winner)向数据x拉动。 eta为学习率.
        eta = basic_eta/i;
        delta = eta*(x_j-clusters(minIdx,:));
        clusters(minIdx,:) = clusters(minIdx,:) + delta;
        acc_err = acc_err + norm(delta);
    end

    if(rem(i,10) ~= 0)
        continue
    end
    figure;
    f = scatter(x, y, 20, 'blue');
    hold on;
    scatter(clusters(:,1), clusters(:,2), 'filled'); % 实心圆点，表示簇心初始位置
    title(['第', num2str(i), '次迭代']);
    if (abs(acc_err-pre_acc_err) < PRECISION)
        disp(['收敛于第', num2str(i), '次迭代']);
        break;
    end

    disp(['累计误差：', num2str(abs(acc_err-pre_acc_err))]);
    pre_acc_err = acc_err;
end

disp('done');

因为学习率eta选得比较随意，以及收敛条件的判断也比较随意，收敛效果只能说还凑合，运行结果：