Codeforces 578B "Or" Game

传送门

You are given $n$ numbers $a_1, a_2, \dots, a_n$. You can perform at most $k$ operations. For each operation, you can multiply one of the numbers by $x$. We want to make $a_1\mid a_2\mid \dots\mid a_n$ as large as possible, where $\mid$ denotes the bitwise OR. Find the maximum possible value of $a_1\mid a_2\mid \dots\mid a_n$ after performing at most $k$ operations optimally.

Input

The first line contains three integers $n$, $ k $ and $ x $ ($1 \le n \le 200000$, $1 \le k \le 10$, $2 \le x \le 8$).
The second line contains $n$ integers $a_1, a_2, \dots, a_n$ ($0 \le a_i \le 10^9$).

Output

Output the maximum value of a bitwise OR of sequence elements after performing operations.

Sample test(s)

input

3 1 2
1 1 1

output

3

input

4 2 3
1 2 4 8

output

79

Note

For the first sample, any possible choice of doing one operation will result the same three numbers 1, 1, 2 so the result is .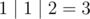

For the second sample if we multiply 8 by 3 two times we'll get 72. In this case the numbers will become 1, 2, 4,72 so the OR value will be 79 and is the largest possible result.

---

Solution

注意到 $2\le x\le 8$，意味着：每次不论选那个数乘以 $x$，这个数的二进制位数都会增加。

（其实这不算什么Key Observation，当 $x>1$ 时，$x$ 乘任何正整数，该数的二进制位数都会增加）

所以要取得最大值，$k$ 次必然都是乘以同一个数，结果的位数就是这个数最后的位数

所以算法是：

将输入数组从大到小排序，枚举乘 $x^k$ 后长度最长的数，更新答案。

为此，预处理出输入数组前缀和后缀取或（|）的结果。

Implementation

#include <bits/stdc++.h>
using namespace std;
const int N(2e5+);
typedef long long ll;
typedef pair<int,int> P;
P a[N];
int f[N], b[N];
int high_bit(ll x){
    for(int i=; i>=; i--){
        if(x&(ll)<<i) return i;
    }
}
int main(){
    int n, k, s;
    scanf("%d%d%d", &n, &k, &s);
    for(int i=, x; i<=n; i++) scanf("%d", &x), a[i]={x, i};

    f[]=;
    for(int i=; i<=n; i++) f[i]=f[i-]|a[i].first;
    b[n+]=;
    for(int i=n; i; i--) b[i]=b[i+]|a[i].first;

    sort(a+, a+n+, greater<P>());
    if(!a[].first){puts(""); return ;}
    ll _=; for(int i=; i<k; i++) _*=s;

    ll ans=, lar=_*a[].first;
    int id, h=high_bit(lar);
    for(int i=; i<=n; i++){
        lar=_*a[i].first;
        if(high_bit(lar)<h) break;
        id=a[i].second;
        ans=max(ans, f[id-]|b[id+]|lar);
    }
    printf("%lld\n", ans);
}

---

比赛时把

typedef long long ll;

写成了

typedef long ll;

结果交上去连样例都没过，但在自己电脑上却没问题, 这是由于 long / long long 的具体长度依赖于机器 (machine-dependent),

C++ 标准只规定了其最小长度（minimum size），long（32 bits）long long（64 bits）.

除去这个细节不谈，比赛时还犯了个算法上的错误：

枚举原来最长的数而不是乘 $x^k$ 后最长的数。

UPD 2018/3/18

难道不是用最大的数乘 $x^k$ 吗？