洛谷—— P1196 银河英雄传说

https://www.luogu.org/problem/show?pid=1196

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成30000列，每列依次编号为1, 2, …,30000。之后，他把自己的战舰也依次编号为1, 2, …, 30000，让第i号战舰处于第i列(i = 1, 2, …, 30000)，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为M i j，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增

大。 然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C i j。该指令意思是，询问电脑，杨威利的第i号战舰与第j号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页……

输入输出格式

输入格式：

输入文件galaxy.in的第一行有一个整数T（1<=T<=500,000），表示总共有T条指令。

以下有T行，每行有一条指令。指令有两种格式：

1. M i j ：i和j是两个整数（1<=i , j<=30000），表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第i号战舰与第j号战舰不在同一列。

2. C i j ：i和j是两个整数（1<=i , j<=30000），表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式：

输出文件为galaxy.out。你的程序应当依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第i 号战舰与第j 号战舰之间布置的战舰数目。如果第i 号战舰与第j号战舰当前不在同一列上，则输出-1。

输入输出样例

输入样例#1：

4
M 2 3
C 1 2
M 2 4
C 4 2

输出样例#1：

-1
1

说明

【样例说明】

战舰位置图：表格中阿拉伯数字表示战舰编号

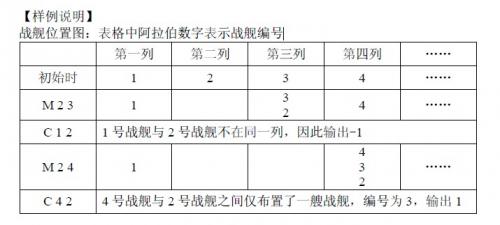
带权并查集，用fro[i]表示在i号船之前的的数量，sum[i]表示第[i]列的数量

每次find时，都需要将fro更新

 #include <algorithm>
 #include <cstdio>
 #include <cmath>

 using namespace std;

 const int N();
 int fa[N],sum[N],fro[N];

 int find(int x)
 {
     if(fa[x]==x) return x;
     int fat=find(fa[x]);
     fro[x]+=fro[fa[x]];
     return fa[x]=fat;
 }
 inline void combine(int x,int y)
 {
     x=find(x),y=find(y);
     fa[x]=y;
     fro[x]+=sum[y];
     sum[y]+=sum[x];
 }
 inline int query(int x,int y)
 {
     int fx=find(x),fy=find(y);
     if(fx!=fy) return -;
     else return abs(fro[x]-fro[y])-;
 }

 int main()
 {
     for(int i=;i<N;i++)
         fa[i]=i,sum[i]=;
     int t,u,v; scanf("%d",&t);
     for(char ch;t--;)
     {
         scanf("\n%c%d%d",&ch,&u,&v);
         if(ch=='M') combine(u,v);
         else printf("%d\n",query(u,v));
     }
     return ;
 }