多校 hdu

欢迎參加——每周六晚的BestCoder（有米！）

Solve this interesting problem

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1571    Accepted Submission(s): 454

Problem Description

Have you learned something about segment tree? If not, don’t worry, I will explain it for you.
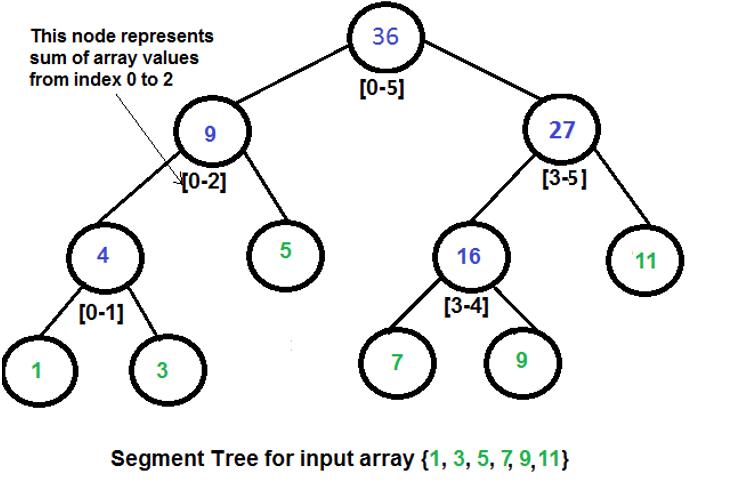
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: Lu and Ru.
- If Lu=Ru,
u is a leaf node. 
- If Lu≠Ru,
u has two children x and y,with Lx=Lu,Rx=⌊Lu+Ru2⌋,Ly=⌊Lu+Ru2⌋+1,Ry=Ru.
Here is an example of segment tree to do range query of sum.

Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value Lroot=0 and Rroot=n contains
a node u with Lu=L and Ru=R.

 

Input

The input consists of several test cases. 
Each test case contains two integers L and R, as described above.
0≤L≤R≤109
LR−L+1≤2015

 

Output

For each test, output one line contains one integer. If there is no such n, just output -1.

 

Sample Input

6 7
10 13
10 11

 

Sample Output

7
-1
12

 

Source

2015 Multi-University Training Contest 3

 

Recommend

wange2014   |   We have carefully selected several similar problems for you:  

pid=5326" style="color:rgb(26,92,200);text-decoration:none;">5326 

pid=5325" style="color:rgb(26,92,200);text-decoration:none;">5325 5324 

pid=5322" style="color:rgb(26,92,200);text-decoration:none;">5322 5321 

 

#include<cstdio>
#include<cmath>
#include<stdlib.h>
#include<map>
#include<set>
#include<time.h>
#include<vector>
#include<queue>
#include<string>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1e-8
#define INF 0x3f3f3f3f
#define LL long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))

LL L, R;
LL flag;

void dfs(LL l, LL r)
{
    if((flag && r >= flag))  return ;
    if(l == 0)
        {
            flag == 0 ? flag = r : flag = min(flag, r);
            return ;
        }
    long long  t = r - l + 1;
    if(t <= l)
    {
        dfs(l - t - 1, r);
        dfs(l - t, r);
        dfs(l, r + t - 1);
        dfs(l, r + t);
    }
}

int main()
{
    while(~scanf("%I64d%I64d", &L, &R))
    {
        flag = 0;
        if(R == 0)
        printf("0\n");
        else
        {
            dfs(L, R);
            if(flag)
            printf("%I64d\n", flag);
            else
            printf("-1\n");
        }
    }
    return 0;
}